
ペンローズのグラフ記法による完全反対称レビチビタテンソルの公式の表現
PDF版は以下から。すべての情報についてPDF版が最新です。noteや他の媒体に比べて導出などを豊富に載せています。
https://lowtonevoice.github.io/math-phys-tech/penrose-notation/main.pdf
必要な知識
この記事では
共変テンソルと反変テンソル(添字の上下)
完全反対称レビチビタテンソル
アインシュタインの縮約記法
クロネッカーのデルタ
についての知識を前提とします。また、「ペンローズのグラフ記法は初めましてです」という方は、以下の記事の「レビチビタ記号の縮約公式」のところまで目を通していただくことをお勧めします。
グラフ記法によるテンソルの表記
一般論
グラフ記法において、テンソルは階数の数だけ"脚"が出たものとして表されます。
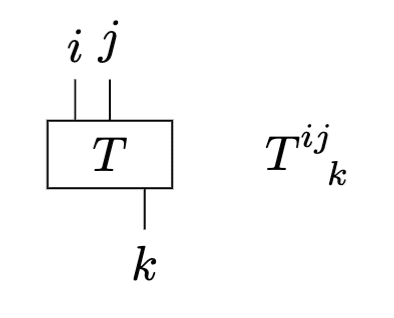
共変と反変の区別も可能です。上向きの脚が出ているものが反変テンソル、下向きの脚が共変テンソルです。
クロネッカーのデルタ
クロネッカーのデルタは両端が開いた脚で表します。
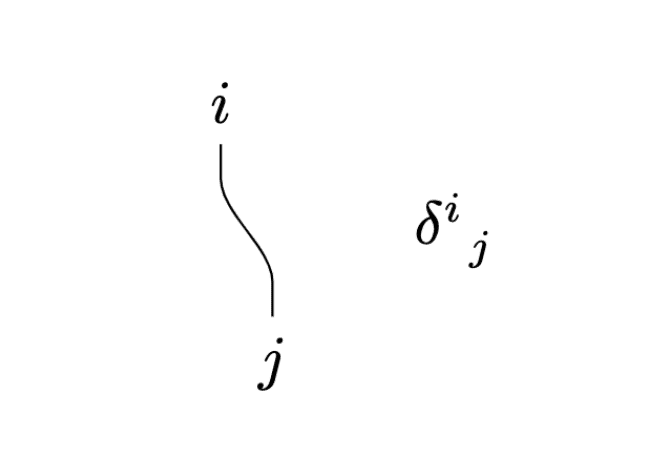
完全反対称レビチビタテンソル
横の太線は反対称性を表します。つまり脚の位置を奇置換すると符号が反転します。これによって完全反対称レビチビタテンソルは以下のように表せます。

本記事では特に反変と共変の積の形$${\epsilon_{ij\cdots k}\epsilon^{pq\cdots r}}$$は、ペンローズの論文に従って次のように表記します。

とはいえ、反変と共変を離して描いた方がわかりやすい場合も多いので、好みや状況に合わせて使い分けてください。
3次元
一般の場合での縮約
$$
\epsilon^{ijk}\epsilon_{pqr}=\left|\begin{matrix}\delta^i_p&\delta^i_q&\delta^i_r\\\delta^j_p&\delta^j_q&\delta^j_r\\\delta^k_p&\delta^k_q&\delta^k_r\end{matrix}\right|
$$
クロネッカーのデルタの記法を使って愚直に書き出すと以下のようになります。

上3点と下3点をもれなくダブりなく繋ぐようにします。すなわち項数は順列$${3!=6}$$です。符号の付け方は「交点がいくつあるか」である程度判別可能です。とはいえ線を迂回させて書けばこのルールを破れますので、「何回の置換によって偶置換の形に戻るか」を考慮するのが安全です。
【補足】
クロネッカーのデルタの行列式自体を完全反対称レビチビタテンソルの定義として採用する流儀もある。これに基づけば上記の結果は自明。
縮約公式
基本的にレビチビタ記号を使う場面では、共変テンソルと反変テンソルのいずれかの添字が揃っている場合が多いはずです。そのときは以下に示すように、揃っている添字をクロネッカーのデルタを表す線でつなげて表せます。
$$
\epsilon^{ijk}\epsilon_{pqk}=\delta^i_p\delta^j_q-\delta^i_q\delta^j_p\;(=\epsilon^{ij}\epsilon_{pq})
$$

2つ以上の添字が揃っている場合は、クロネッカーのデルタを取っている添字について順序の自由度がありますので、順列がつきます。
$$
\epsilon^{ijk}\epsilon_{pjk}=2!\delta^i_p\;(=\epsilon^i_p)
$$
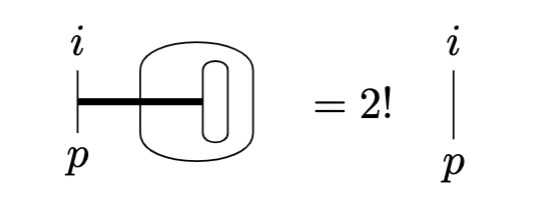
$${\epsilon^i\epsilon_p=\delta^i_p}$$なのはいうまでもないでしょう。添字が全て揃うと$${\epsilon^{ijk}\epsilon_{ijk}=3!}$$となりますね。
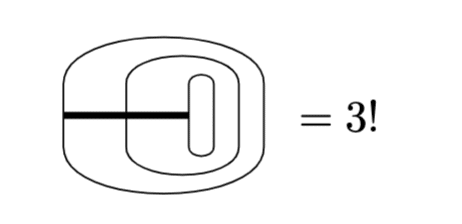
4次元
特に相対論で使うミンコフスキー計量にて符号が変わるので注意が必要ですが、それを除けば3次元の場合と同じになります。
基本の場合
一般に行列式を使ってこのように表されますね。
$$
\epsilon^{ijkl}\epsilon_{pqrs}=\left|\begin{matrix}\delta^i_p&\delta^i_q&\delta^i_r&\delta^i_s\\\delta^j_p&\delta^j_q&\delta^j_r&\delta^j_s\\\delta^k_p&\delta^k_q&\delta^k_r&\delta^k_s\\\delta^l_p&\delta^l_q&\delta^l_r&\delta^l_s\\\end{matrix}\right|
$$
3次元と同様、愚直に書き出すとこのようになります。

これだけの量になると、アルゴリズムに従って書き出さないと重複や抜けが生じてきますのでご注意を。
縮約公式
3次元同様に縮約公式が取れます。
$$
\epsilon^{ijkl}\epsilon_{pqrl}=\epsilon^{ijk}\epsilon_{pqr}=\left|\begin{matrix}\delta^i_p&\delta^i_q&\delta^i_r\\\delta^j_p&\delta^j_q&\delta^j_r\\\delta^k_p&\delta^k_q&\delta^k_r\end{matrix}\right|
$$

全て展開するよりも完全反対称レビチビタテンソルを残しておく方が賢明ですね。
係数のつき方も3次元同様です。
$$
\epsilon^{ijkl}\epsilon_{pqkl}=2!\epsilon^{ij}\epsilon_{pq}=2(\delta^i_p\delta^j_q-\delta^i_q\delta^j_p)
$$

$$
\epsilon^{ijkl}\epsilon_{pjkl}=3!\epsilon^i\epsilon_p=6\delta^i_p
$$
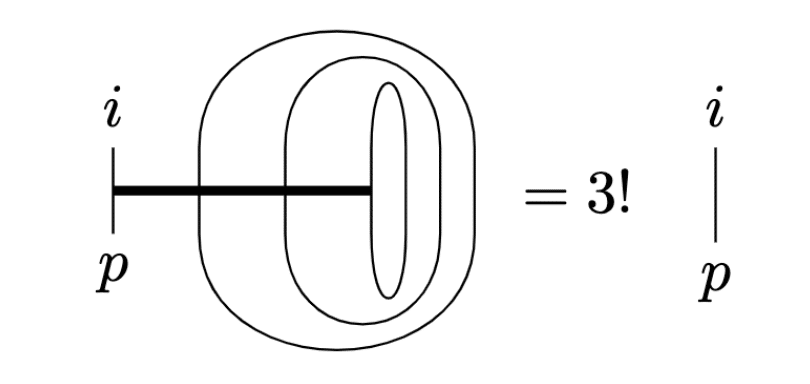
全て添字が揃うと$${\epsilon^{ijkl}\epsilon_{ijkl}=4!=24}$$となります。

ミンコフスキー計量(相対論)
上記の議論はユークリッド計量$${g_{ij}=g^{ij}=\delta_{i,j}}$$の元で成り立つ話です。ミンコフスキー計量においては計量テンソル$${g_{ij},g^{ij}}$$の空間3成分または時間1成分が$${-1}$$であるために、共変テンソルと反変テンソルで符号が逆転しますね。
$$
\epsilon_{pqrs}=g_{ip}g_{jq}g_{kr}g_{ls}\epsilon^{ijkl}=-\epsilon^{pqrs}
$$
従って、上で与えた4次元の結果とは全て符号が反転します。従って
$$
\begin{array}{l}\epsilon^{ijkl}\epsilon_{pqrs}=-\left|\begin{matrix}\delta^i_p&\delta^i_q&\delta^i_r&\delta^i_s\\\delta^j_p&\delta^j_q&\delta^j_r&\delta^j_s\\\delta^k_p&\delta^k_q&\delta^k_r&\delta^k_s\\\delta^l_p&\delta^l_q&\delta^l_r&\delta^l_s\\\end{matrix}\right|\\\epsilon^{ijkl}\epsilon_{pqrl}=-\epsilon^{ijk}\epsilon_{pqr}=-\left|\begin{matrix}\delta^i_p&\delta^i_q&\delta^i_r\\\delta^j_p&\delta^j_q&\delta^j_r\\\delta^k_p&\delta^k_q&\delta^k_r\end{matrix}\right|\\\epsilon^{ijkl}\epsilon_{pqkl}=-2!\epsilon^{ij}\epsilon_{pq}=-2(\delta^i_p\delta^j_q-\delta^i_q\delta^j_p)\\\epsilon^{ijkl}\epsilon_{pjkl}=-3!\epsilon^i\epsilon_p=-6\delta^i_p\\\epsilon^{ijkl}\epsilon_{ijkl}=-4!=-24\end{array}
$$
となります。ミンコフスキー計量は4次元テンソルにおいてのみ適用されますから、縮約すると同時に符号が変わります。
一般次元の一般計量
ここまでの一般化として、以下のように縮約が取れます。

また一般の計量をもつ$${d}$$次元リーマン多様体では
$$
\epsilon^{\mu_1\cdots\mu_d}=g^{\mu_1\nu_1}\cdots g^{\mu_n\nu_d}\epsilon_{\nu_1\cdots\nu_d}=\det(g^{-1})\epsilon_{\mu_1\cdots\mu_n}
$$
が成り立つので、例えば以下のようにできる。

参考文献
"Applications of Negative Dimensional Tensors" Roger Penrose
「場の古典論 (原書第6版)」ランダウ=リフシッツ
使用例
テンソルとしての役割ではありませんが、行列式や逆行列、余因子展開が直観的に表せます。
テンソルとしてのレビチビタ記号は微分形式で大活躍します。
より具体的な系での使用例はこちら。
