
【随時更新】 Probability and Statistics (確率統計) - 英単語チートシート
大学院の授業が始まり、はじめは知識を英語で理解しようとしましたが、早々に断念しました。
そもそも専門用語の英単語そのものを知らなかったり、これって日本で習ったあれだよな?という感じで結局調べることになるためです。
今の私の英語力(IELTS 6.5)では、英語を英語のまま理解できる範囲に限りがあります。薄い理解のまま貴重な授業を終わらせないよう、日本語に翻訳して理解を図ることも多々あります。
そんなことをしていると、頻出/重要英単語の翻訳表が欲しい気持ちが高まってきました。
そこで今回は「Probability and Statistics (確率統計)」の英単語の日本語訳を記事にまとめてみようと思います。
私自身のための記事ですが、もし同じ思いを共にする方がいたらお気軽にご活用ください。
注釈: 本記事では各言葉の定義については解説しません。
各言葉の内容は別のWebサイトや教材等を参考にしてください。
英単語シートのみを閲覧したい方は「Probability」の章以降をご覧ください。目次は授業の進行順に記載しています。
授業の参考書は以下のとおりです。
はじめに:授業の概要
オールボー大学で今セメスター受講している「Probability and Statistics」は、「Lecture and Exercise(講義と演習)」と「Workshop(実践)」を組み合わせた授業です。
「Lecture and Exercise(講義と演習)」
およそ2時間の講義を受け、その後およそ2時間演習に取り組みます。オールボー大学の(少なくともエネルギー工学科の)授業は、基本的にこの「1授業約4時間」という時間割が標準になっています。
(Problem-based Learning を基点にした学習方法として、この方式を採用しているようです。詳しくは別の記事に書こうと思います。)
授業は朝8時15分から始まるので、お寝坊に注意が必要です。日本人は時間に正確と思われているのでなおさら!
講義資料は大学のWEBサービス(履修管理システム的なもの)に公開されています。本科目ではシラバスと講義資料を読むところ、確率変数、確率分布など基本的な確率論に始まり、標本調査、推定、仮説検定、回帰分析、確率過程を学習するようです。
講義資料がアップロードされていることもあってか、前半の授業部分はスラスラ進みます。単語でつまづいて翻訳しているうちに次のトピックへ…ということを幾度も経験しました😅
演習は、R言語を用いて参考書の課題演習を解くという時間です。この時間は講義室を離れ、Problem-based Learning プロジェクトのグループメンバー共同で行います。わからないことがあればここで質問しあって解消することができます。オールボー大学独自の授業スタイルのようなのですが、これがめちゃくちゃありがたいです。
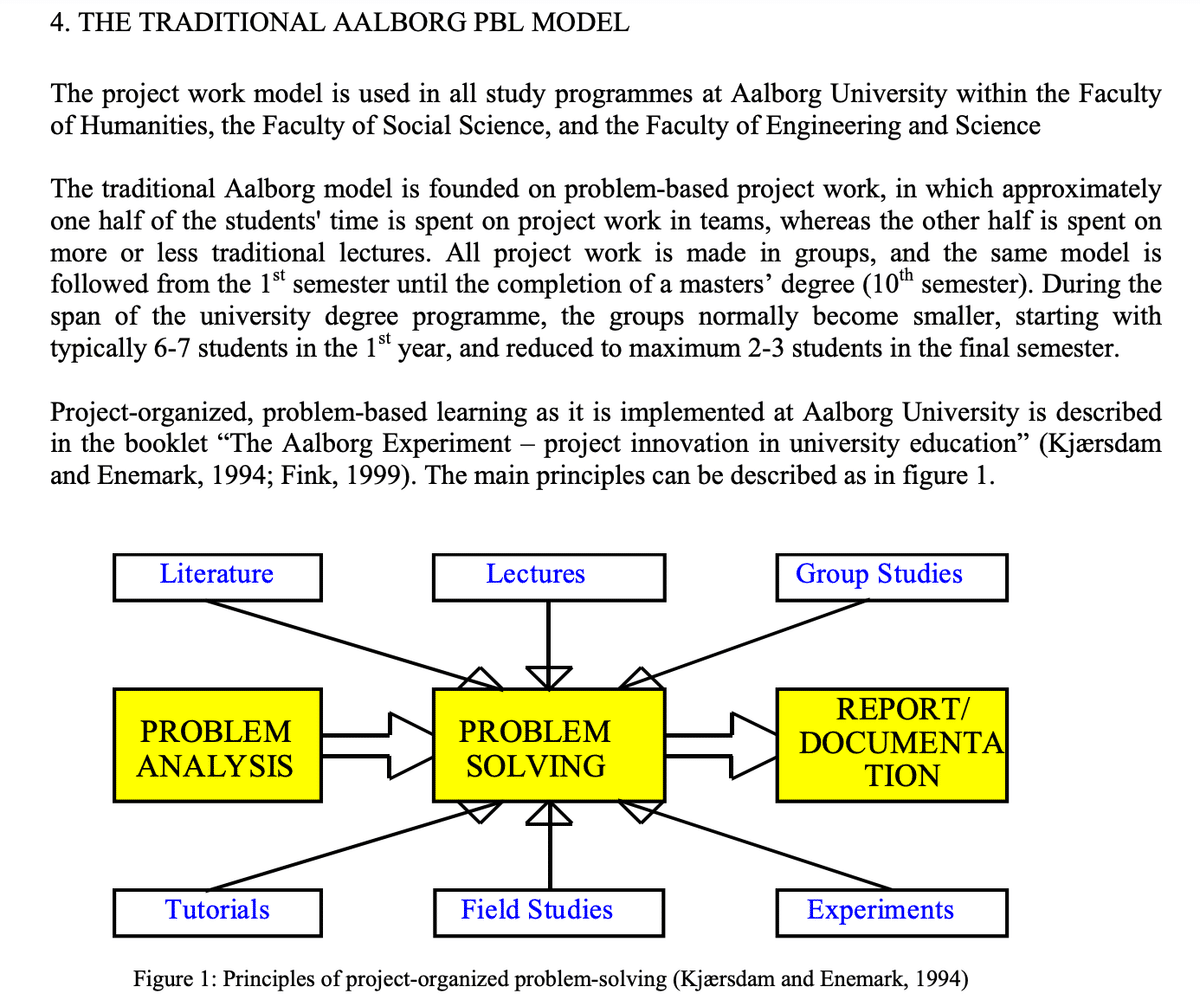
講義とグループ学習が織り込まれているとのこと
Anette K. et. al, : "THE AALBORG MODEL - PROBLEM-BASED AND PROJECT-ORGANIZED LEARNING" (2004), https://homes.plan.aau.dk/ak/PBL/kap2-introductionTHE%20AALBORG%20MODEL.pdf
演習時間中は講義の先生やTAの方が巡回してくれていて、個人やグループ全員がわからないことを聞くことができます。
講義の先生に何度か質問しましたが、私はここでも先生のマシンガントークで話に置いていかれています。英語と数学、ダブルわからない。。。
「Workshop(実践)」
Workshopは課題演習の拡張版という形で、4時間の授業時間全てを使って演習問題を解きます。Workshopは「Lecture and Exercise(講義と演習)」単元の区切りごとに1回設けられています。単元は後述の章立てと等しく、Probability など合計で4単元あります。
「Examination(試験)」
とても驚いたのですが、この科目の試験は「Oral(口頭)」試験となっています。シラバスと現地学生の話によれば、試験の内容は「Workshopで解いた4単元の問題群のうちランダムで出題される1単元を口頭で解説する」という内容のようです。
つまり小手先の暗記は通用せず、英語でどのように解いたかを説明しなければいけないので、確率統計の英単語を覚えていないと詰むことになります😇
続けて、現在覚えるのに苦戦しているものを含めた、確率統計の英単語群を記載していきます。
Probability
Introduction to Probability
Event : 事象
Sample space : 標本空間
Union : AかつB
Intersection : AまたはB
Probability : 事象が起こる確率 P(A)
Mutually exclusive : 相互に排他的 P(A and B) = 0
Probability of complement : 余事象 P(A^c) =1 - P(A)
Conditional probability : 条件付き確率
Independent Event : 独立事象
Stochastic Variable
Stochastic variable : 確率変数
Discrete stochastic variables (Discrete random variables) : 離散型確率変数
Continuous stochastic variables : 連続型確率変数
Probability function : 確率関数
Distribution function : 分布関数
Mean (expected value) : 平均
Variance : 分散
Standard deviation : 標準偏差
Continuous stochastic variables
Probability density function : 確率密度関数
The uniform distribution : 一様分布
Two random variables
Joint probability function : 同時確率関数
Joint distribution : 同時分布
The marginal probability function : 周辺確率関数
Marginal density function: 周辺分布関数
Covariance : 共分散
Correlation : 相関
Distribution
Binomial distribution : 二項分布
Normal distribution : 正規分布
Standard normal distribution : 標準正規分布
Z-score : Zスコア
Sampling
Population : 母集団
Sample : 標本
Observation : 観測
Statistical inference : 統計的推論
Sample proportion : 母比率
Summary statistics : 要約統計
Sample mean : 標本平均
Standard error : 標準誤差
Central limit theorem : 中心極限定理
Sample variance : 標本分散
Sample standard deviation : 標本標準偏差
T-score : tスコア
T-distribution : t分布
Degrees of freedom : 自由度
Descriptive statistics
Descriptive statistics 記述統計学
Quantitative variables: 量的変数
Categorical variables (qualitative variables): カテゴリ変数
Percentiles: パーセンタイル(分位)
Interquartile Range: 四分位範囲
Box plot : 箱ひげ図
Scatter plot : 散布図
Quantile - Quantile plot (Q-Q plot) : Q-Q プロット
Point and interval estimates
Point estimation : 点推定
Interval estimation : 区間推定
Consistency : 一致性
Efficiency : 効率性
Unbiasedness : 不遍性
Consistent estimator : 一致推定量
Confidence Interval : 信頼区間
Confidence level : 信頼度 100(1 − α) [%]
Error probability : エラー確率 α = 1 − Confidence level [%]
Critical value : 臨界(境界)値
Confidence interval for the variance
Chi-square distribution : カイ二乗分布
Determining sample size
Margin of error : 許容誤差
Hypothesis Test
Hypothesis and test
Hypothesis : 仮説
Significance test ; 優位性検定
The null hypothesis : 帰無仮説 H_0
The alternative hypothesis : 対立仮説 H_a
Test statistic : 検定統計量
P-value : P値
Statistically significant : 統計的に優位な
Comparison of two populations
Two samples are Independent : 対応なし
Two samples are paired : 対応あり
Linear Regression
The Regression Problem
Regression : 回帰
Response: 応答
Explanatory variable (predictor) : 説明変数
Simple regression : 単回帰
Intercept : 切片
Slope : 傾き
Linear regression : 線形回帰
Random Error : 偶然誤差
Least square method : 最小二乗法
Regression equation (Prediction equation) : 回帰方程式
Residuals: 残差
Sum of squared errors (SSE) : 残差平方和
Standardized regression correlation : 標準回帰係数
R-squared: Reduction in prediction error
Total sum of square (TSS) : 総平方和
Fraction of explained variation, or the Multiple coefficient of determination (R-squared) : 決定係数 R^2 = (TSS - SSE)/TSS
Multiple regression model
Multiple regression : 重回帰
Simpsons Paradox : シンプソンのパラドックス
The general model
Partial regression coefficients : 偏回帰係数
Interaction : 相互作用
Multiple R-squared
F-test : F検定
Multicollinearity : 多重共線性
Dummy variable : ダミー変数
Stochastic Process
Basic of Stochastic Process
Stochastic Process : 確率過程
Stochastic variable : 確率変数 𝑋_𝑡
White noise : ホワイトノイズ𝑊_𝑡(𝑋_𝑡 が平均0, 分散σ^2)
Gausian noise : ガウスノイズ X_t ~ norm(0, σ^2)(正規化ホワイトノイズ)

Random walk : ランダムウォーク 𝑋𝑡=𝑋𝑡−1+𝑊𝑡
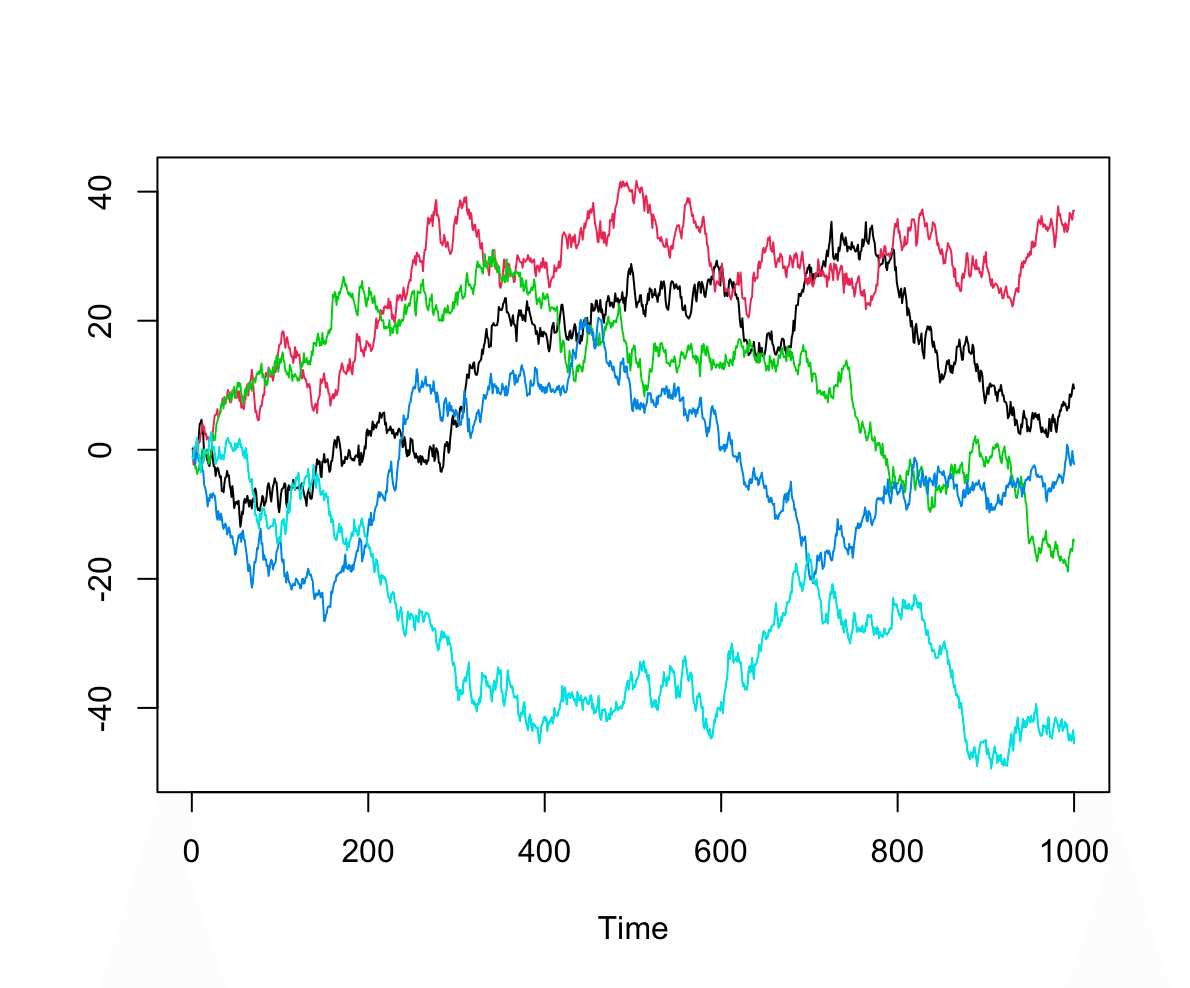
First order autoregressive process (AR(I)): 一次自己回帰過程
𝑋_𝑡 = 𝛼𝑋_(𝑡−1)+𝑊_𝑡Autoregressive coefficient 𝛼 : 自己回帰係数 −1<𝛼<1
Backshift operator (𝐵) : 後退オペレータ 𝐵𝑋_𝑡=𝑋_(𝑡−1)
Polynomial : 多項式
Characteristic equation : 特性方程式 1 − 𝛼_1 𝑧 − 𝛼_2 𝑧^2 −⋯− 𝛼_𝑝 𝑧^𝑝 = 0
Akaike’s Information Criterion (AIC) : 赤池情報量基準
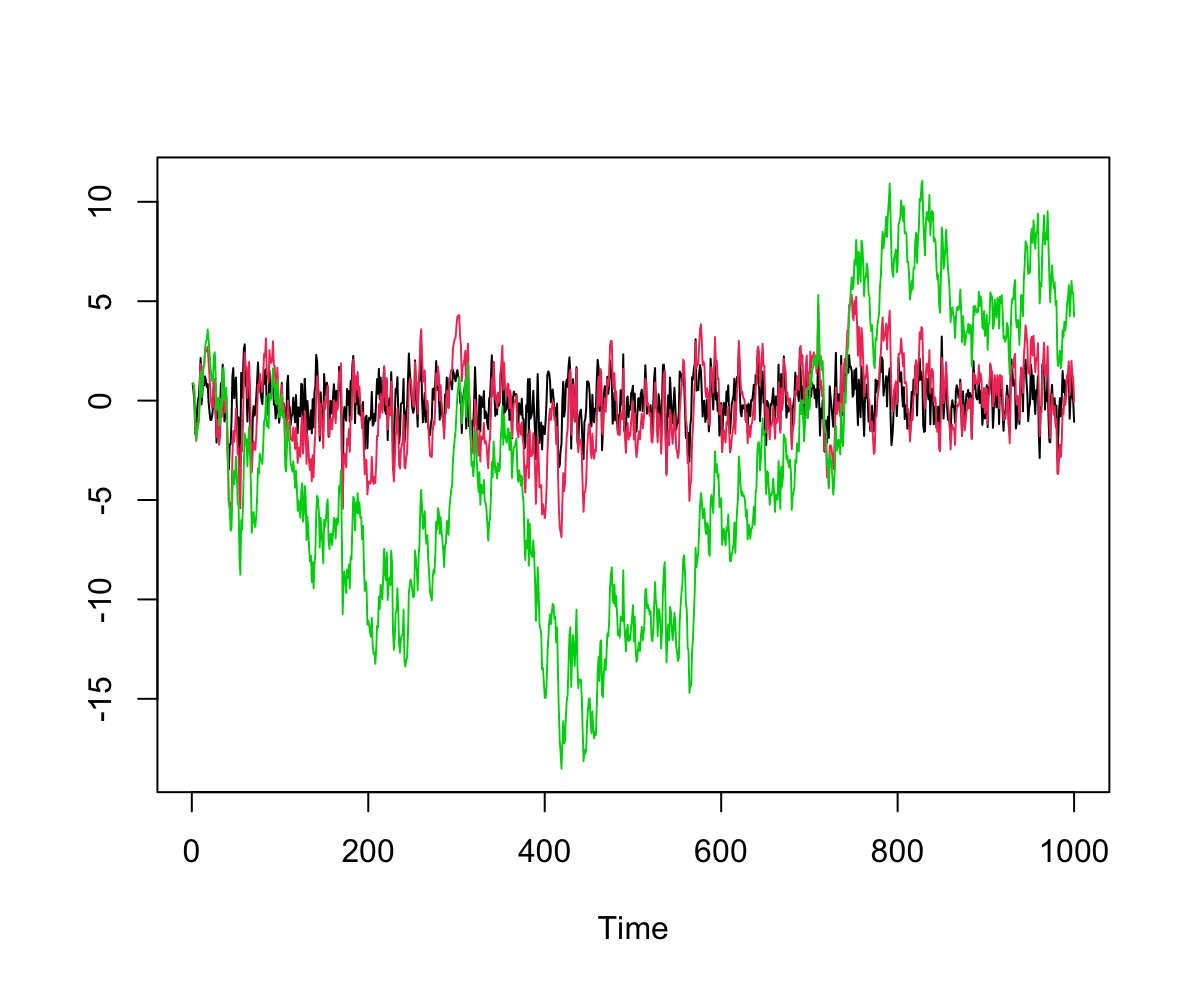
black : 𝛼 = 0.5
red : 𝛼 = 0.9
green : 𝛼 = 0.99 (≒ random walk)
Mean function : 平均関数 𝜇𝑡=𝔼(𝑋𝑡)
Stationary : 定常
First order stationary : 一次定常性 𝑋_𝑡=𝛼𝑋_𝑡−1+𝑊_𝑡 となる
Second order stationary : 二次定常性 𝜌(𝑡,𝑡+ℎ)=𝜌(ℎ) となる
Autocovariance function : 自己共分散関数
𝛾(𝑡,𝑡+ℎ) = Cov(𝑋_𝑡,𝑋_(𝑡+ℎ)) = 𝔼((𝑋_𝑡 − 𝜇_𝑡)(𝑋_(𝑡+ℎ) − 𝜇_𝑡+ℎ))lag : ラグ(時間の遅れ)
Autocorrelation function (ACF) : 自己相関関数
𝜌(𝑡,𝑡+ℎ)=Cor(𝑋_𝑡,𝑋_(𝑡+ℎ))=Cov(𝑋_𝑡,𝑋_(𝑡+ℎ)) / (𝜎_𝑡 𝜎_(𝑡+ℎ))correlogram : コレログラム(lag vs ACF のグラフ)
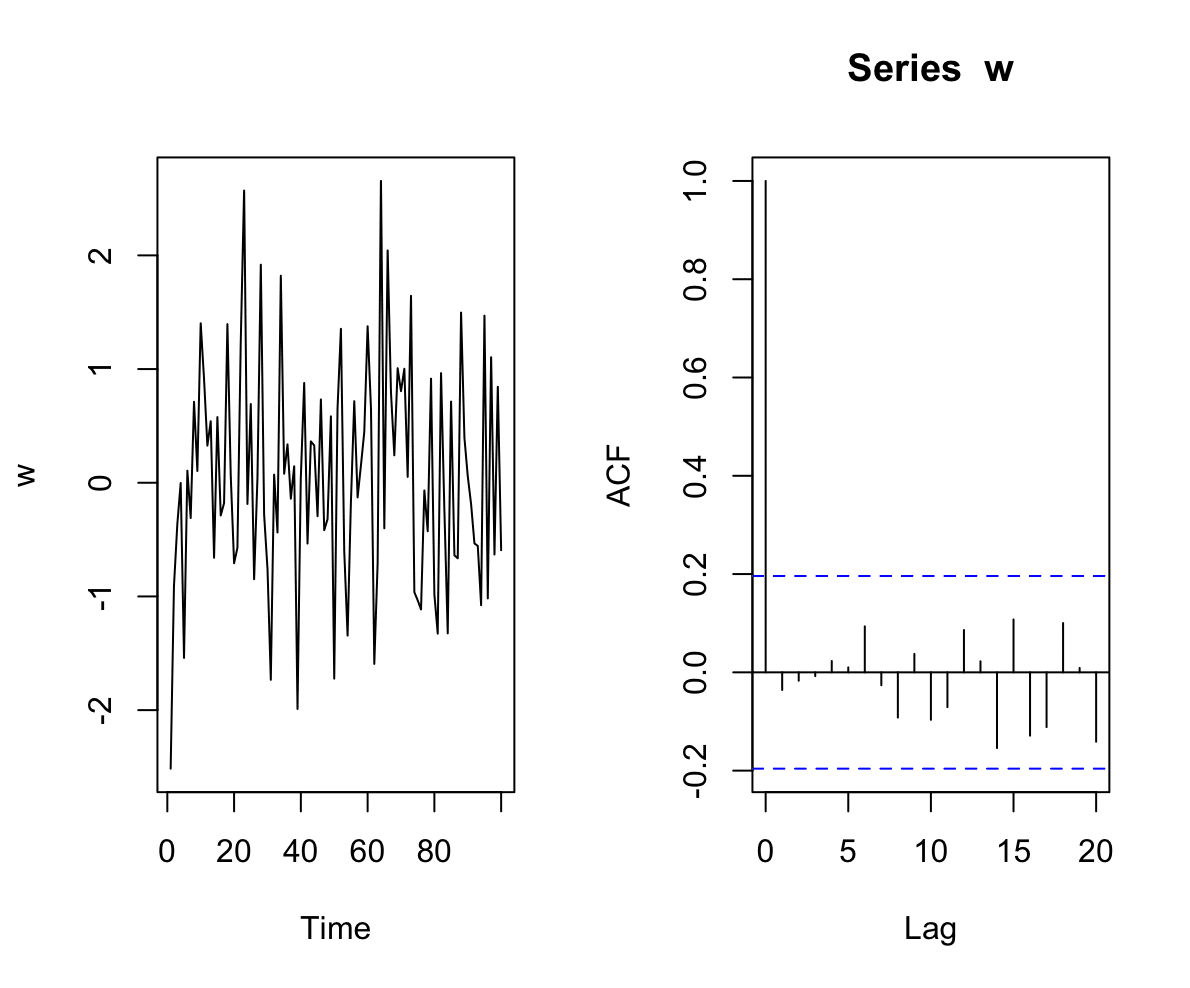
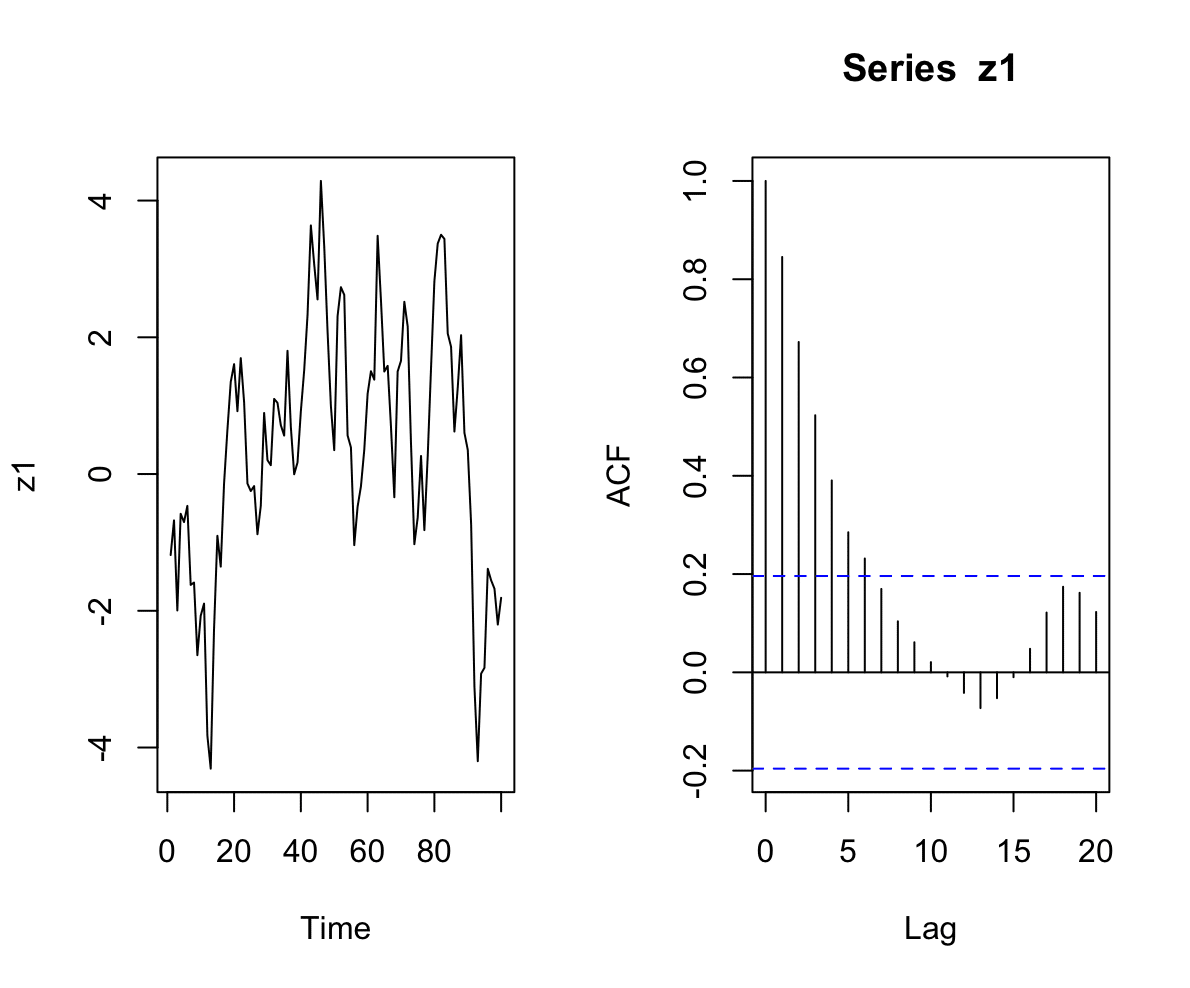
Non-stationary : 非定常
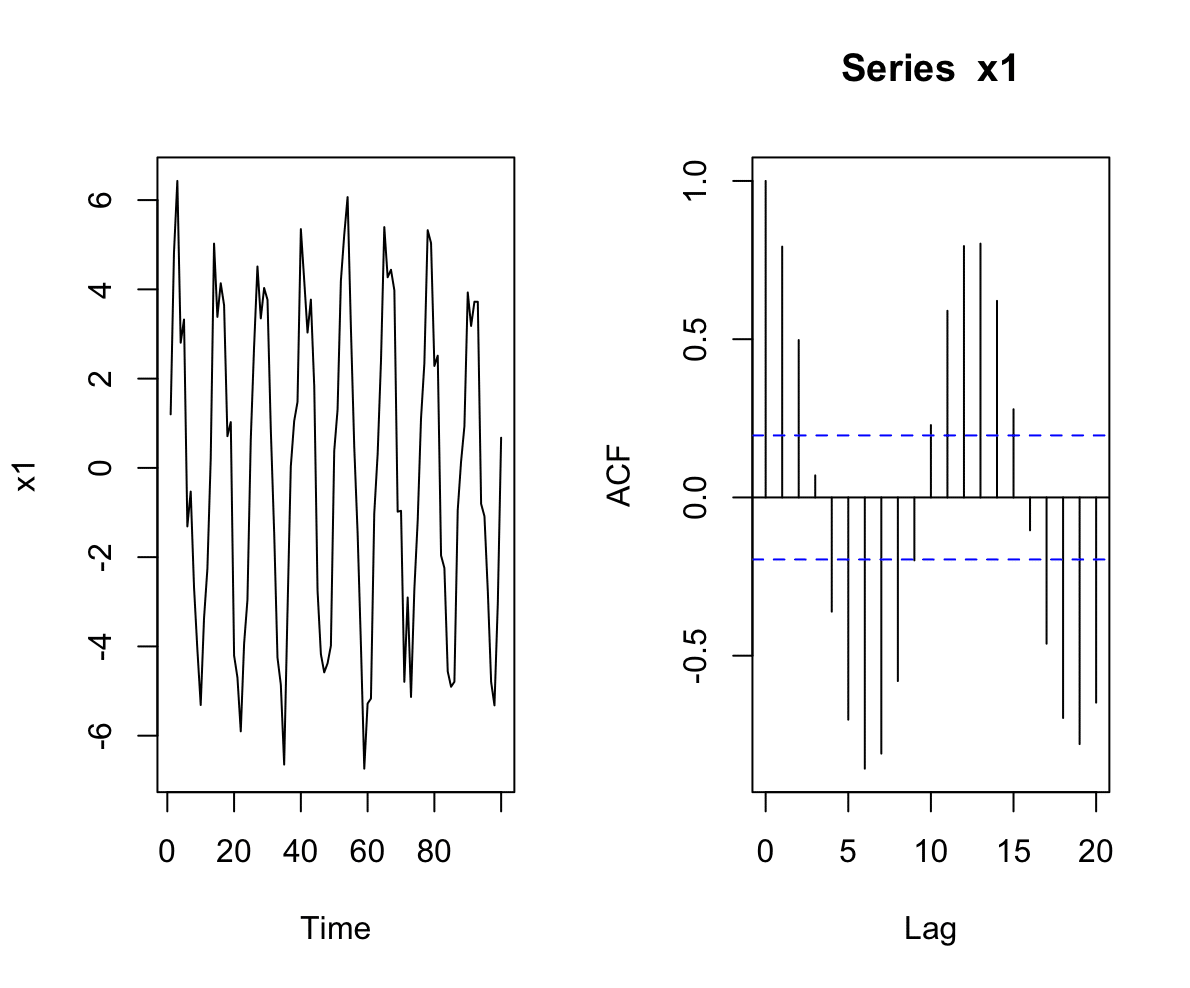
moving average : 移動平均
Advance
Stochastic trend
Time series of differences ∇X_t = X_t - X_(t-1)
Integrated of order : 和文過程の定常
Maximum likelihood estimation method (MLE) : 最尤推定(さいゆう推定)
Empirical : 経験的な(≒ practical)
Autoregressive–moving-average (ARMA) model : 自己回帰移動平均モデル
Auto Regressive Integrated Moving Average (ARIMA) : 自己回帰和文移動平均モデル
Advance
Exogenous variable : 外生変数
Cross correlation function : 相互相関係数
ARMAX (An alternative way of including exogenous variables into an ARMA) : 外生変数付きARMA
Wiener process : ウィーナー過程
Brownian motion : ブラウン運動
Stochastic differential equation (SDE) : 確率微分方程式
drift coefficient : ドリフト係数
diffusion coefficient : 拡散係数
授業の進み具合に応じて随時更新予定です。
おまけに
確率統計は高専時代になんとなく学んだ以来、なんだか掴みきれないまま今まで来てしまっていたので、このタイミングで学び直せるのはありがたい限りです。本科目の履修前後の筆者を比較した場合の「確率統計の知識量と活用具合の平均値に変化がない」という帰無仮説(H_0)を棄却できるように頑張ります😉
いいなと思ったら応援しよう!

