
【論文レビュー】縦断研究を学ぶ初学者にやさしい論文:岡林(2006)
縦断研究を学ぶならこの論文がわかりやすいですよ!とオススメいただいた論文を読んでみました。たしかに理解しやすいので、縦断研究をやらねば…という初学者の方は、騙されたと思って(?)ぜひ読んでみてください。
岡林秀樹. (2006). 発達研究における問題点と縦断データの解析方法. パーソナリティ研究, 15(1), 76-86.
二時点データの分析
まず、xとyという変数の間に因果関係があると推定するための三つの条件について、著者は石塚(1984)を基に整理してくれています。
xとyの間に共変動(相関関係)がある
xとyの間に時間的順序を特定できる
xとyの双方に影響を与える変数の影響を取り除いてもxとyの共変動は0にならない
因果関係がある!と言うことは非常に難しく、このように整理してくれているのは大変ありがたいです。
このような二時点のデータをSEM(構造方程式モデリング)による分析モデルに組み込み、交差遅延効果モデルか同時効果モデルの統計的手法を用いて分析することができるとしています。それぞれ、図で捉えた方が視覚的にイメージしやすいので貼っておきます。
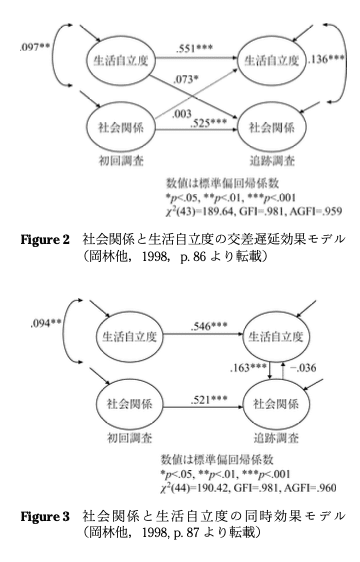
三時点以上のデータ分析
三時点以上のデータを分析する際には潜在成長曲線分析が活用できます。本論文では、「3時点以上でデータを測定した場合において、個人ごとの加齢に伴う変化のパターンを推定し、さらには、ある変数の変化のパターンに対する他の変数の影響や、2つ以上の変数の変化のパターンどうしの関係を検討する方法」(p.81)と説明されています。
より一般的な説明としては、豊田先生編著の『共分散構造分析[Amos編]』では「縦断的データに含まれる変数の、変化の様相を分析することに特化したモデル」(p.100)とされています。
一次関数なら理解できる!?
SEMのモデルとしてはこんな感じになります。

これは、切片=αで傾き=βの一次関数で表せるようです。潜在成長曲線モデルの特長は、この切片と傾きをさらに従属変数や独立変数とするモデルに分解することができることにあります。

一次関数にしてもらえると、中学校の数学レベルで理解できるのでほんとにありがたいです!
