
基礎編26.5 「偶然3つ以上の分母⑥」一方から1つ・もう一方から2つ取り出す
2022年に2つの県の公立で出題されて、どこかに分類というよりも、一つのパターンとしておいた方がいいと思うので(無理やり挿入して小数点になりますが)独立した項目として掲載しておきます。
右の図のように,袋Aと袋Bの2つの袋がある。袋Aには1,3の数字が1つずつ書かれた2個の玉が入っており,袋Bには1,3,4の数字が1つずつ書かれた3個の玉が入っている。袋Aからは1個の玉を,袋Bからは同時に2個の玉を取り出し,取り出した3個の玉を用いて次のようにして得点を決めることにした。
・取り出した3個の玉に書かれた3つの数がすべて異なるときは,その3つの数の和を得点とする。
・取り出した3個の玉に書かれた3つの数のうち2つの数が同じときは,その2つの数の積と残り1つの数との和を得点とする。
このとき、得点が奇数になる確率を求めなさい。ただし,どの玉が取り出されることも同様に確からしいものとする。

偶然は何回起こっている?
2袋あるので、偶然も2回起こる、と考えてしまいがちですが、分担できる偶然は分担しつくしてしまいましょう。そうすると
●袋Aから取り出す人・・・1人(Aさん)
●袋Bから取り出す人・・・1人1個の玉で分担すれば、2人(B(ビー)さん&β(ベータ)さん)
のあわせて3人でこの偶然を構成することができます。
偶然3つですから、「同様に確からしい」出来事を数えるには、表ではなく樹形図をかきます。ところが、この樹形図の書き方が曲者。
樹形図をかいてみましょう。まず、Aさんにとって起こる偶然は[1]と[3]の2通り。Bさんにとって起こる偶然は[1][3][4]の3通り。Aさんに起こる偶然は、Bさんに起こる偶然に影響を及ぼしませんから、ここまでのところで樹形図をかくと、こんな感じ。
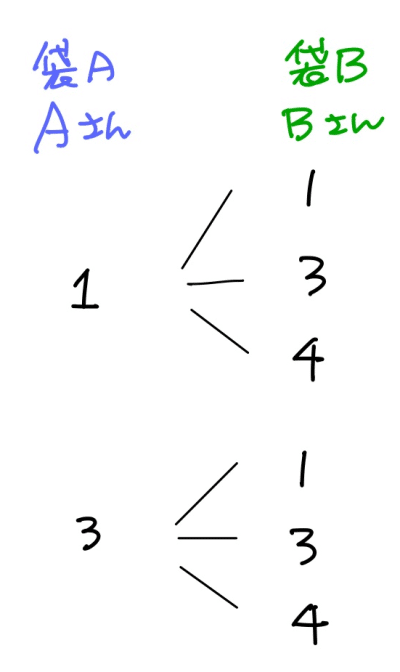
考え方その1
さて、βさんも袋Bから取り出します。Aさんの偶然とは影響しませんが、Bさんが取り出した玉はβさんは取り出すことができません。というわけで、この発想で行くと、樹形図はこのようになります。

このように考えると、すべての場合の数は12になります。

点数を計算してそれが奇数になるのは4通りなので、求める確率は$${\dfrac{4}{12}=\bm{\dfrac{1}{3}}}$$です。
これで終わりでよいのですが・・・
考え方その2
解法の研究がこのnoteの目的ですので、もう少しスマートな方法もある、というのをやります。Bさんとβさんは同時に取り出すのでした。Aさんのことがなければ、こういうことになります。
そうするとBさんとβさんの取り出す順序は関係なくなりますので、ここはこのような樹形図をシンプルにして考えてもよい、ということになります。(樹形図が部分的にC型になる、ということです)

というわけで、それぞれについて点数を計算してみると、すべての場合が6で、そのうち基数の点数になるのは2通りですので、答えは$${\dfrac{2}{6}=\bm{\dfrac{1}{3}}}$$で求めることができます。
考え方1で起こることの2つ分を1つにまとめて考えています。このことがピンとくると、「その1」の方法で求めた確立と同じになるのはわかりますね。
考え方その3
さて、ここからは上級編の考え方になります。ポイントは何か、というと、「同様に確からしいこと」を全部並べること。そのために図や表を使うんでした。
まず袋Bで起こることを整理してから、袋Bと袋Aとでの偶然を掛け合わせること、という順番で考えてみましょう。
そうすると、こういう樹形図をかいてもよさそうです。(答えは同じなので省略)

考え方その4
考え方その3で考えた樹形図、もうちょっと考えると、
袋Bで取り出すのは〔1-3〕〔1-4〕〔3-4〕の3通り、ということになります。これは袋B’に〔1-3〕〔1-4〕〔3-4〕と書いた3つの玉が入っていて、その中から1つだけ取り出すことである、と考えてしまってもよいでしょう。

そうすると、袋B’と袋Aとで考えればよい、ということであれば、あら、偶然は2つ、ということになりますので表で考えることができます。

以上、ちょっとしつこい感じになりましたが、上級を目指す人であれば、いろんな考え方を引き出しに入れておいてほしい、と考えて、アプローチを並べてみました。数学は自由だ、と言われるのは、答えの近づき方が正しければ、一見近づき方が違っていても、同じところにたどり着く、ということでもあるのです。その”自由さ”を手に入れるためには、いろんな近づき方ができるようにするのがよくて、そのためには、いろいろな近づき方を知っておくとよいわけです。
問題を解いたあとに・・・
で、こっちから1つ、こっちからは2つで、合わせて3つを取り出すというパターンは、(今はなき)大学入試センター試験でも出題されていました。
二つの箱A,Bがある.
Aの箱には,次のように6枚のカードが入っている.
0の数字が書かれたカードが1枚
1の数字が書かれたカードが2枚
2の数字が書かれたカードが3枚
Bの箱には,次のように7枚のカードが入っている.
0の数字が書かれたカードが4枚
1の数字が書かれたカードが1枚
2の数字が書かれたカードが2枚
Aの箱から1枚,Bの箱から2枚,あわせて3枚のカードを取り出す.
(1) 3枚のカードに書かれた数がすべて0である確率は$${\dfrac{\fbox{シ}}{\fbox{スセ}}}$$である.
(2) 3枚のカードに書かれた数の積が4である確率$${\dfrac{\fbox{ソ}}{\fbox{タチ}}}$$である.
(3) 3枚のカードに書かれた数の積が0である確率は$${\dfrac{\fbox{ツテ}}{\fbox{トナ}}}$$である.
(以下略)
表をかく気力さえあれば、上と同じやり方で解けます。表の考えに基づきながら、しかし実際に表をかかずにいろいろ考えられるようになれば、それが大学入試レベル、ということになります。(もちろんガッツで表をかいても可能です) 挑戦したい人には、答えだけ示しておきましょう。
(シ~ナは、それぞれ記号1つに数字が1つ対応していて、マークシートを塗りつぶして解答するという形式です。)
$${\dfrac{\fbox{シ}}{\fbox{スセ}}=\bm{\dfrac{1}{21}}}$$,$${\dfrac{\fbox{ソ}}{\fbox{タチ}}=\bm{\dfrac{4}{63}}}$$,$${\dfrac{\fbox{ツテ}}{\fbox{トナ}}=\bm{\dfrac{37}{42}}}$$
-----------------------
<前の問題 次の問題>
問題一覧
この記事が気に入ったらサポートをしてみませんか?
