
神奈川県|公立高校入試統計問題2023
ある中学校で1学年から3学年まであわせて10クラスの生徒が集まり生徒総会を開催した。生徒総会では生徒会から3つの議案X,Y,Zが提出され,それぞれの議案について採決を行った。
右の資料1は議案Xに賛成した人数を,資料2は議案Yに賛成した人数を,それぞれクラスごとに記録したものである。資料3は議案zに賛成した人数をクラスごとに記録し,その記録の平均値,中央値,四分位範囲をまとめたものである。
このとき,次の(i),(ii)に答えなさい。
資料1 (単位:人)
19 21 13 17 25
24 17 17 23 14
資料2 (単位:人)
20 26 19 27 25
24 20 15 24 20
資料3 (単位:人)
平均値 23
中央値 21
四分位範囲 6
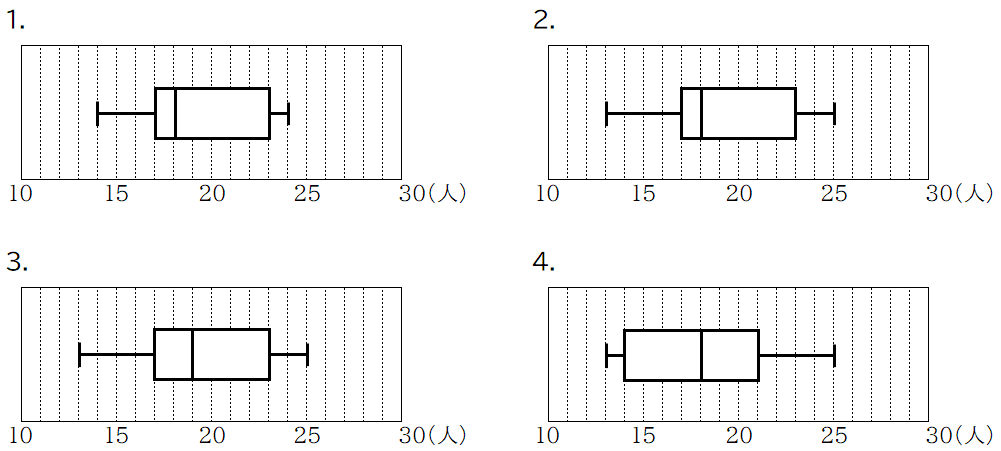
(i) 資料1の記録を箱ひげ図に表したものとして最も適するものを次の1~4の中から1つ選び,その番号を答えなさい。
(ii) 資料2と資料3から読み取れることがらを,次のA~Dの中からすべて選び,その記号を答えなさい。
A.議案Yに賛成した人数の最頻値は20人である。
B.賛成した人数の合計は,議案Zより議案Yの方が多い。
C.賛成した人数の中央値は,議案Zより議案Yの方が大きい。
D.賛成した人数の四分位範囲は,議案Zより議案Yの方が小さい。
(解答方式を組合せの選択肢から改題)
(i)データから箱ひげ図
まず、資料1を、データの値が小さい順に並べ替え、中央値・第1四分位数・第3四分位数を求めます。
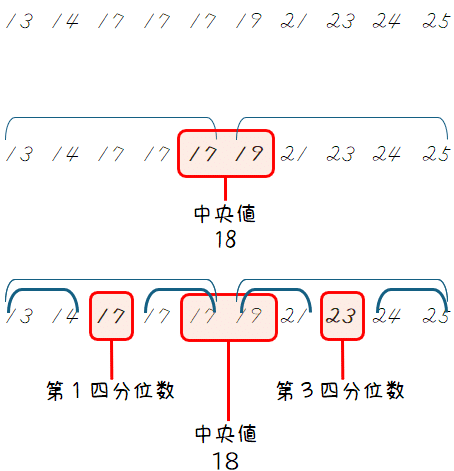
箱ひげ図に必要な5つのデータを整理すると

この5つのデータすべてがあっているものは

2番です。
(ii)
1つ1つ見てみましょう。
最頻値
最頻値とは、データの値の中でもっとも多く現れる値のことです。議案Yに賛成した人数を表しているのが資料2ですから、このデータを見ると、

確かに、20人がいちばん多く現れています。この選択肢は正しいですね。
データの合計
議案Yに賛成した人数を表している資料2のデータの値を、すべて合計すると220。
議案Zについては資料3を見ますが、平均値が23で、データ数は10クラス分10個ありますから、その合計は23×10=230。
この選択肢は間違いですね。
中央値
議案Yについての資料2のデータを小さい順に並べると、

議案Yに賛成した人の中央値は20と24の平均ですから22。確かに議案Yの中央値の方が大きいですから、この選択肢も正しいです。
四分位範囲
議案Yについての資料2のデータを、小さい順に並べると、

四分位範囲は第3四分位数と第1四分位数の差ですから、25-20=5。確かに、議案Yの方が議案Zより、賛成した人の四分位範囲は小さい。
答
(i) 2 (ii) A,C,D
この記事が気に入ったらサポートをしてみませんか?
