
山梨県|公立高校入試確率問題2024
箱の中に,赤球2個,青球1個,白球2個が入っている。この箱の中から球を同時に2個取り出したとき,取り出した球の中に青球が含まれる確率を求めなさい。
ただし,どの球を取り出すことも同様に確からしいものとする。
分類:20 見た目同じことが起こる偶然-色玉
同じ確率で起こることがらは何か?
中学校での確率の問題の根本にあるのは「同じ確率で起こる場合」を並べることです。
この問題の箱の中から球を1個取り出したとき,「同じ確率で起こる場合」は
× 赤球を取り出すこと
× 青球を取り出すこと
× 白球を取り出すこと
ではありません。赤球2個に1・2,青球に3,白球2個に4・5と番号を振っておくと
○ 赤球1を取り出すこと
○ 赤球2を取り出すこと
○ 青球3を取り出すこと
○ 白球4を取り出すこと
○ 白球5を取り出すこと
が,それぞれに同じ確率で起こることがらです。
これらをもとに,偶然2つ「同時に2個取り出したとき」を考えます。
表の縦・横に「同じ確率で起こる場合」をそれぞれかきましょう。同時に2個取り出すので,たとえば取り出した球が2つとも3の球ということはあり得ませんので,対角線を消します。また同時に2個なので順序は関係ありませんので,対角線の右上側と左下側は2つ1組で考えられます。左下側の方を消して考えることにします。

起こりうるすべての場合は10通りだということがわかります。そのうち,青球が含まれるのは
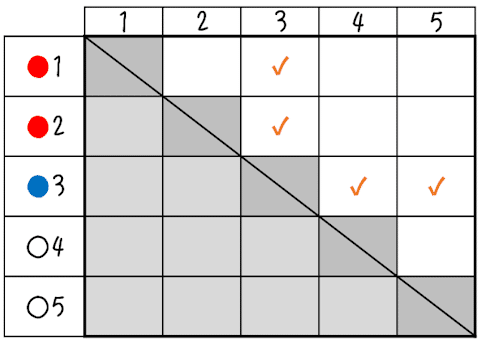
印をつけた{1,3},{2,3},{3,4},{3,5}の4通りですから,求める確率は$${\dfrac{4}{10}=\dfrac{2}{5}}$$となります。
答
$${\bm{\dfrac{2}{5}}}$$
同様に確からしい?
どの場合が起こることも同じ程度であると考えられるとき,同様に確からしいといいます。
ぶっちゃけて言うと,同様に確からしいということは,どの場合も同じ確率で起こる,ということなのですが,確率とは何か?の話をする前に確率の話が出てきてしまうことになるので,数学の専門家には評判の悪い考え方です。
でもいったん「確率」まで習ってしまっているので,同じ確率で起こることがらのことを同様に確からしいことがらと読み替えているのだ,ということで,ここでは説明をしてしまいます。
この記事が気に入ったらサポートをしてみませんか?
