×兵庫県｜公立高校入試確率問題2021

　随所で指摘していることだが、公立高校の入試問題の中でも兵庫県の問題だけは、学習指導要領の解説で「樹形図や二次元の表などを利用して、起こり得るすべての場合を簡単に求めることができる程度の事象」とされている範囲を超えることがあります。果たして今年度は・・・

　６枚のメダルがあり，片方の面にだけ１，２，４，６，８，９の数がそれぞれ１つずつ書かれている。ただし，６と９を区別するため，６は６＿、９は９＿と書かれている。数が書かれた面を表，書かれていない面を裏とし，メダルを投げたときは必ずどちらかの面が上になり，どちらの面が上になることも同様に確からしいものとする。
　この６枚のメダルを同時に１回投げるとき，次の問いに答えなさい。
（１）　２枚が表で４枚が裏になる出方は何通りあるか，求めなさい。
（２）　６枚のメダルの表裏の出方は，全部で何通りあるか，求めなさい。
（３）表が出たメダルに書かれた数をすべてかけ合わせ，その値を$${a}$$とする。ただし，表が１枚も出なかったときは，$${a}$$＝０とし，表が１枚出たときは，そのメダルに書かれた数を$${a}$$とする①　表が出たメダルが１枚または２枚で，$${\sqrt{a}}$$が整数になる表裏の出方は何通りあるか，求めなさい。②　$${\sqrt{a}}$$が整数になる確率を求めなさい。

分類　融合Ａ２平方根

“まじめに”解きます

　偶然は6回起こるので，文科省カリキュラムに縛られている中学生は樹形図を書いて考えるしかありません。まじめに樹形図を書いてみましょう。

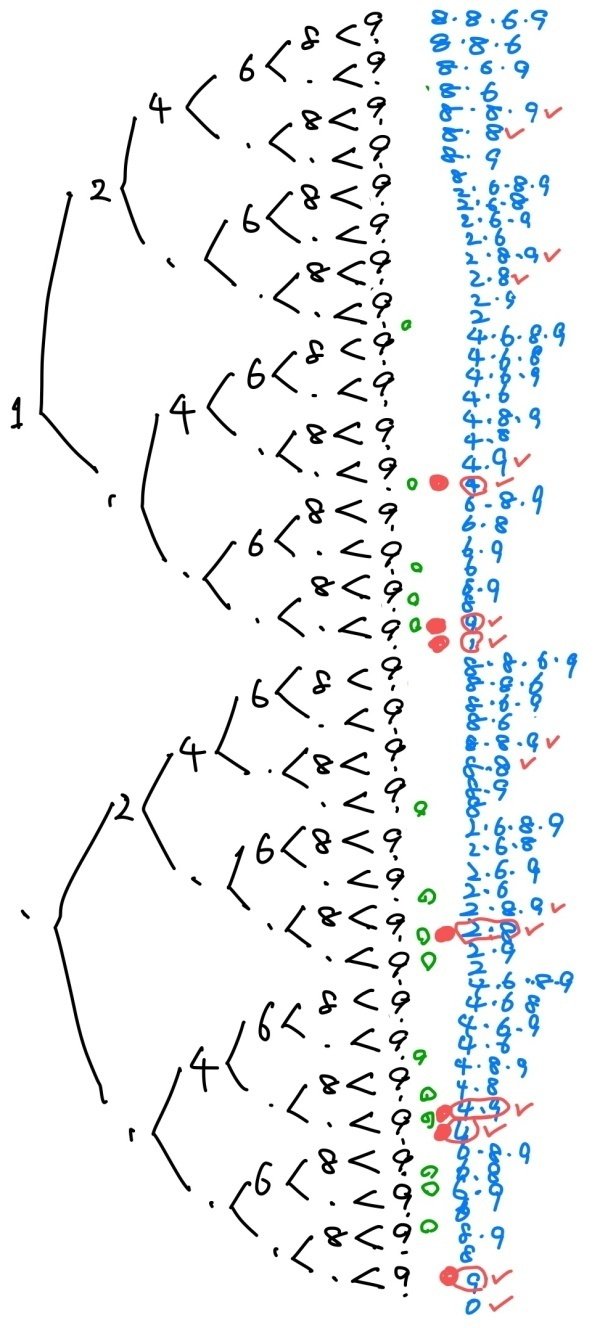
（1）2枚が表で4枚が裏、という組は上の樹形図の緑の○印、あわせて15通りになります。
（2）樹形図の最後の枝を全部数えると64通り。
（3）①表が出たメダルが１枚または２枚で，$${\sqrt{a}}$$が整数になるのは、図の赤○印で、合わせて7通り。
②　$${\sqrt{a}}$$が整数になるのは、①の場合も含めて，図のチェック印の16通りで，すべての場合の数は（2）より64通りですので、求める確率は$${\dfrac{16}{64}=\bm{\dfrac{1}{4}}}$$

答

（１）１５通り　（２）６４通り
（３）①７通り　　②　$${\bm{\dfrac{1}{4}}}$$

・・・なんて解き方をしろとでもいうのだろうか？

　さすがに，これだけの樹形図を書くのは鬼です。分母は「計算・公式で求める（❷）」，分子は「独自列挙で求める（②）」のやり方で解かないと時間がありません。

（1）は6枚のうちから順序関係なく表になる2枚を選び出す場合の数と同じ、と考えると、C型の表が書けます。（枠の中の数は(3)で使います）

（2）は、①のメダルが裏表になる場合が2通り、それぞれについて②のメダルが裏表になる場合が2通り、さらにそれぞれについて④のメダルが裏表になる場合が2通り、そしてそのそれぞれについて⑥のメダルが裏表になる場合が2通り、そのまたそれぞれについて⑧のメダルが裏表になる場合が2通り、そのそれぞれについて⑨のメダルが裏表になる場合が2通り，というわけで，すべての場合の数は$${2×2×2×2×2×2(=2^6)=\bm{64}}$$と計算で求めることができます。

(3)①は、表が1枚の場合と表2枚の場合に分けて考えましょう。表2枚の場合は(1)で列挙していて、そのうち$${\sqrt{a}}$$が整数になるのは｛1,4｝｛1,9｝｛2,8｝｛4,9｝の4通り、表が1枚で$${\sqrt{a}}$$が整数になるのは①，④，⑨の3通りで、合わせて7通りと求めることができます。

②は、①で考えていない表が0枚、3枚、4枚、5枚、6枚のときについて考えて、たしあわせればよいでしょう。
　表が0枚のときは1通りしかなく、$${a}$$＝０になるのでしたから、$${\sqrt{a}=0}$$で整数になります。
　表が3枚のときは樹形図を書いて考えましょう。｛1,2,8｝｛1,4,9｝｛2,4,8｝｛2,8,9｝の4通りあります。

　表が4枚のときは、裏が2枚ですからその裏が2枚のときの表をかいて考えてみましょう。｛2,4,8,9｝｛1,2,8,9｝｛1,2,4,8｝の3通りが条件を満たします。

　表が5枚の場合は6枚のメダルのうちどれかが裏ということですから、やはり6通りあり、そのうちで$${\sqrt{a}}$$が整数になるのは｛1,2,4,8,9｝の1組だけ。
　そして表が6枚のときは$${\sqrt{a}}$$は整数にならない。
　したがって、7＋1＋4＋3＋1＝16で、$${\sqrt{a}}$$が整数となる組み合わせは合わせて16通りある、ということになります。

　文科省のカリキュラムとして想定している方法で解くには時間がかかりすぎる問題で、少なくとも公立高校の入試問題として適しているのか疑問がある、ということは繰り返しておきます。

【研究】もっと、もっと！

　ここまでくると確率の問題、というよりも平方根の問題ですが、$${\sqrt{a}}$$が整数になるには、
●②と⑧のメダルがいっしょに表になるか，いっしょに裏でないといけない●⑥のメダルが表だと、絶対整数にならない
ということですから
［１］［２・８］［４］［９］から選べば、必ず平方数（$${\sqrt{a}}$$が整数）になります。
　　　１つも選ばない　１通り
　　　１つ選ぶ　４通り
　　　２つ選ぶ　６通り
　　　３つ選ぶ（どれか１つ選ばない）　４通り
　　　４つすべて選ぶ　１通り
　これで合わせて１６通りです。

【研究】樹形図をサボる

　メダルのうち①については、表が出ようが裏が出ようが、かけ算の答は変わりません。唯一変わるのは、①のコイン以外がすべて裏の場合だけですね。ですから、残りの１５通りについては、結果は同じですから×２をすればよい、と考えても，樹形図を半分にして１６通りだけ書いて、①のコイン以外がすべて裏の場合だけ気をつける，というやり方をしてもよいでしょう。そうすると，ギリ「簡単に図表が書ける範囲」におさまるのかな・・・