
大分県|公立高校入試確率問題2024
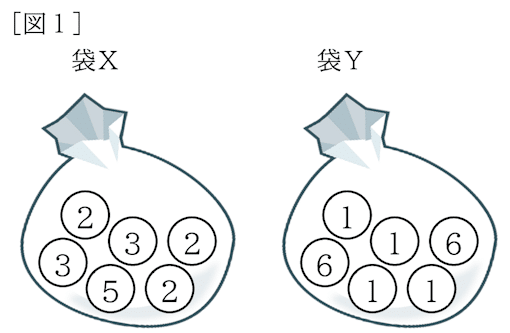
右の[図1]のような2つの袋X,Yがある。
袋Xの中には,2の数字が書かれた玉が3個と,3の数字が書かれた玉が2個と,5の数字が書かれた玉が1個入っている。
袋Yの中には,1の数字が書かれた玉が4個と,6の数字が書かれた玉が2個入っている。
太郎さんと花子さんの2人が,それぞれ次のように2回玉を取り出す。
[太郎さんの取り出し方]
・1回目は,袋Xから玉を1個取り出し,玉に書かれている数字を確認する。
・取り出した玉を,袋Xにもどしてよく混ぜる。
・2回目は,ふたたび袋Xから玉を1個取り出し,玉に書かれている数字を確認する。
[花子さんの取り出し方]
・1回目は,袋Xから玉を1個取り出し,玉に書かれている数字を確認する。
・2回目は,袋Yから玉を1個取り出し,玉に書かれている数字を確認する。
ただし,袋Xからどの玉を取り出すことも,袋Yからどの玉を取り出すことも,それぞれ同様に確からしいものとする。
次の①,②の問いに答えなさい,
① [太郎さんの取り出し方]において,1回目に取り出す玉に書かれている数字が,2回目に取り出す玉に書かれている数字より大きくなる確率を求めなさい。
②次の(P),(Q)の確率において,確率が大きい方は(P),(Q)のどちらであるか,1つ選び,記号を書きなさい。
また,選んだ方の確率を求めなさい。
(P)[太郎さんの取り出し方]において,1回目に取り出す玉に書かれている数字が,2回目に取り出す玉に書かれている数字より小さくなる確率
(Q)[花子さんの取り出し方]において,1回目に取り出す玉に書かれている数字が,2回日に取り出す玉に書かれている数字より小さくなる確率
分類:21 見た目同じことが起こる偶然-かぶり数字玉
玉は区別してから表をかく
2と書かれた玉が3個ありますので,どのことがらが起こることも「同様に確からしい」ようにするために,この3個の玉を区別しておきます。ここでは2と②と[2]として,区別できるようにしておきます。
同様に,3と書かれた玉も2個ありますので,3と③としておいて,表をかきます。取り出して戻してもう1回ですから,表は次のようになります。

起こりうるすべての場合の数は36通りで,1回目が2回目よりも大きくなる(1回目より2回目が小さくなる)のは,次の表のようになり,11通り。
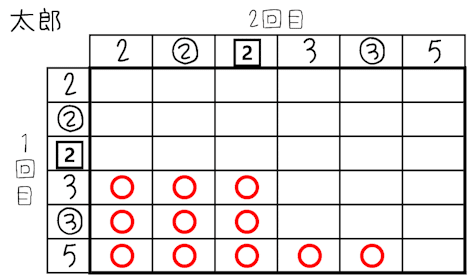
ですから,求める確率は$${\dfrac{11}{36}}$$です。
確率を比べる
PとQの確率を比べるために,それぞれの確率を求めましょう。
注意が必要なのは①の問題の太郎さんは「1回目が2回目よりも大きくなる」確率を考えるのに対し,②の問題では「1回目が2回目よりも小さくなる」確率です。ヒヤッとしますね。(結果として値が一緒で,どうしてこんなひっかけを埋め込んだのかはわかりませんが)
袋Yの1の玉・6の玉も複数入っていますので,区別をつけて表をかくことにします。また,花子さんは,1回目を袋Xから,2回目を袋Yから取り出しますので,そこにも注意を払うこと。

P(太郎さん)の確率は$${\dfrac{11}{36}}$$,Q(花子さん)の確率は$${\dfrac{12}{36}=\dfrac{1}{3}}$$で,花子さんの確率の値の方が(わずかに)大きいですので,Q $${\dfrac{1}{3}}$$と答えればよいわけです。
答
① $${\bm{\dfrac{11}{36}}}$$ ② Q $${\bm{\dfrac{1}{3}}}$$
1つ1つは基礎的な問題なのですが,文章をよく読んで状況をつかんで,区別して考えないといけないし,ひっかけ・ひっかかりポイントもあるので,数学よりも国語力が試されている感じもします(が,どうも状況が人工的ないので,思考力・判断力・表現力等の育成に対応した出題,というのも,ちょっとどうなのでしょう?)
この記事が気に入ったらサポートをしてみませんか?
