
茨城県|公立高校入試確率問題2020
右の図のように,正五角形ABCDEがあり,点Pは,はじめに頂点の位置にある。1から6までの目のある2個のさいころを同時に1回投げて,出た目の数の和だけ,点Pは左回りに頂点を順に1つずつ移動する。例えば,2個のさいころの出た目の数の和が3のときは,点Pは頂点Dの位置に移動する。
2個のさいころを同時に1回投げるとき,点Pが頂点Eの位置に移動する確率を求めなさい。
ただし,それぞれのさいころにおいて1から6までのどの目が出ることも同様に確からしいとする。

表をつくったらどうする?
さいころ2個なので、とりあえず表を作って、和を計算しておきましょう。

ここからです。2個のさいころの出た目の数の和に応じて、点Pの位置は変わりますので、それぞれ調べましょう。
2個のさいころの出た目の数の和が2のとき→点Pは頂点Cの位置
3 → D
4 → E
5 → A
6 → B
7 → C
8 → D
9 → E
10 → A
11 → B
12 → C
なので、点Pが頂点Eの位置に移動するのは、2つのさいころの目の和が4と9のとき。表に書き込むと
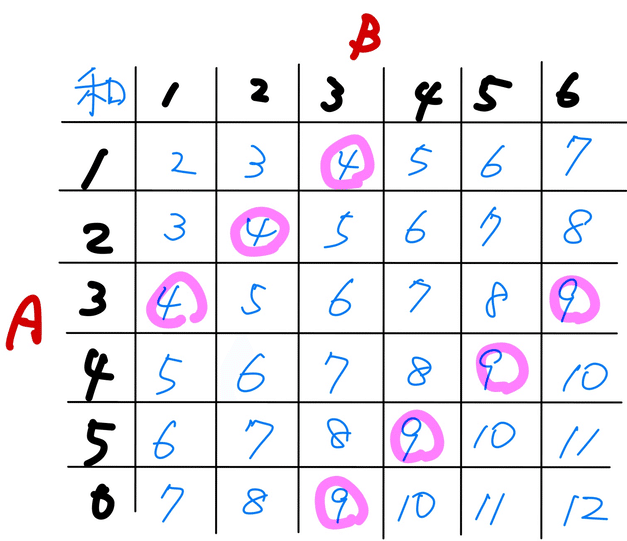
となるので、あてはまる場合の数は7通り、求める確率は$${\dfrac{7}{36}}$$となります。
答
$${\bm{\dfrac{7}{36}}}$$
問題を解いたあとに(解く前に?)
もちろん「5でわったあまり」に注目して
上の解説で和が2のとき、3のとき・・・でイチイチ確かめていたことにイライラした人もいるかも知れません。点PがEの位置に行くのは、2つのさいころの目の和を「5でわったときに4あまるヤツ」なのです。
この手の「循環型」の問題は、「あまりに注目する」というのがお決まりの解法です。
もちろん、問題パターンとその解法をたっぷり覚えておくことも大切なのですが、しかしもっと根本で大切なのは,上でやったように泥臭く解いたり試行錯誤したりする中で「お決まりの解法」の意味を知って、使えるものとして自分の使える道具にしていくことです。
解法パターンより,少ない武器でも問題に立ち向かう勇気。
この記事が気に入ったらサポートをしてみませんか?
