三重県-前期選抜｜公立高校入試確率問題2021

　大小２つのさいころを同時に投げ，出た目の数をそれぞれ$${a，b}$$とする。このとき，次の各問いに答えなさい。ただし，さいころの目の出方は，１，２，３，４，５，６の６通りであり，どの目が出ることも同様に確からしいものとする。

①　$${a－b}$$の値が３となる確率を求めなさい。

②　$${\sqrt{ab}}$$の値が自然数となる確率を求めなさい。

③　右の図のように，正方形ＡＢＣＤがある。点Ｐは点Ａを出発してＢ，Ｃ，Ｄ，Ａ，Ｂ，…の順に$${a}$$だけ，点Ｑは点Ａを出発してＤ，Ｃ，Ｂ，Ａ，Ｄ，…の順に$${b}$$だけ各頂点を移動して止まる。
　このとき，点Ｐと点Ｑが同じ頂点に止まる確率を求めなさい。

分類：①１０　その他四則　②９　積が○　
③応用❷（他のものを動かす、循環型）

①は表をかこう

　さいころ2つなので、起こりうるすべての場合を表すのに表をかくと便利です。各マス目に$${a－b}$$の値も書いておきましょう。

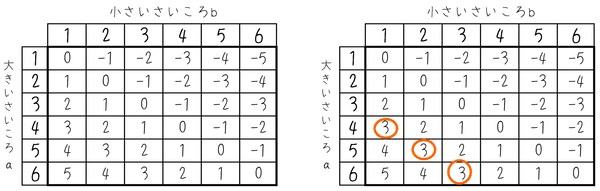
　起こりうるすべての場合は３６通りで、そのうち$${a－b}$$の値が３となるのは３通りありますから、求める確率は$${\dfrac{3}{36}=\bm{\dfrac{1}{12}}}$$となります。

②も表。各マス目に何を入れる？

　さいころ2つなので、起こりうるすべての場合を表すのに表をかくと便利です。各マス目に$${\sqrt{ab}}$$の値をいちいち入れると、ちょっと面倒そう。$${ab}$$は簡単に求められますので、この値を記入して、$${\sqrt{ab}}$$が自然数になる場合に〇印をつけるのが、早いかな。

　起こりうるすべての場合は３６通りで、そのうち$${\sqrt{ab}}$$の値が自然数となるのは８通りありますから、求める確率は$${\dfrac{8}{36}=\bm{\dfrac{2}{9}}}$$となります。

③は、どこにいるかを書き添えて

　③も、さいころ２つを使う問題ですが、①・②とちょっと毛色が違います。「さいころ２つの結果を使って、ほかのものを操作する」問題、このシリーズでは《応用》と分類しているタイプの問題です。
　点Ｐ・点Ｑが移動する先をそれぞれ書き添えておいて、比べることにしましょう（左）。すると、点Ｐと点Ｑが同じ頂点に止まる場合は９通りあることがわかります。

　確率は$${\dfrac{9}{36}=\bm{\dfrac{1}{4}}}$$と求めることができます。

答

（１）　$${\bm{\dfrac{1}{12}}}$$　　　（２）　$${\bm{\dfrac{2}{9}}}$$　　　　（３）　$${\bm{\dfrac{1}{4}}}$$