
÷1桁の0の扱い(4) 「たてる・かけるの0」と省略算 |基礎計算研究所
「たてる・かけるの0」
「たてる・かけるの0」は、商の各位に0が立つ場合であり、たてるの0とかけるの0をまとめたのは、その位に0がたてば,0をかけるので自動的にかけるにも0があらわれる。セットにして扱ってよい。
また、たてる・かけるの0は、「ひくの0」「おろすの0」に比べて「特殊感」が強い。0を立てたときに、ここに0を書いてよいのか、0と書いた場合に(省略算含めて)次どうするのか、ほかの各ステップに比べると特殊感が強いと考えて、
ひくの0 < おろすの0 < たてるの0
の順を定めることにする。
アルファベット記号で言うと、xとoである。
頭位に商がたたないものも「たてる・かけるの0」
もうひとつ、頭位に商がたたないものも「たてる・かけるの0」に分類しておく。つまり「たてる・かけるの0」には、さらに細かく分類すると
●頭位に0が立つ(頭位に商がたたない)
●中位・末位に0が立つ
の2つが分類されている,と見ることができる。ただ頭位に商がたたないのは「頭位に0が立つ」のを省略の0として扱うことで、統一的に見ることができるのである。

この頭位に0が立たないものの扱いは、教科書によって異なっている。たとえば啓林館の教科書では、各桁の商に0が立つもの・からむものをまとめて扱い、中位に0が立つ642÷6の計算に並べて252÷6を例題として示し、キャラクターに「はじめの0はかかなくていいです。」とコメントさせている。(p46)
ところが、東京書籍と学校図書は整商の桁数で節を分けていて、百の位に商がたたないものとして、商3桁と商2桁を分けて扱っている。
この代表的な3社で表にしてみる。

「たてる・かけるの0」と省略算
特に、中位・末位の省略算について、見ておきたい。
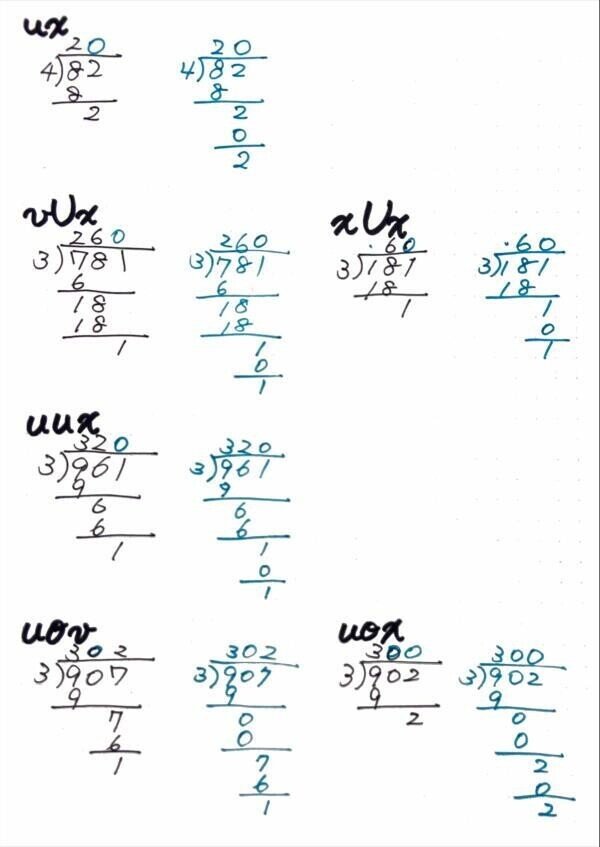
東京書籍は3桁÷1桁ではじめて省略算を示すが、学校図書では2桁÷1桁ですでに省略算を示している。啓林館では「商に0がたつときのかんたんなしかた」を囲みにくくり出して、省略算を説明している。
東京書籍・啓林館では一通り練習してから省略算を示し、そのあと教科書にそのための練習問題はない。省略算は習得可能な子ができればよい、という扱いに思われる。
省略算については、おろすの0で言及してあったuo[*]型についても触れておく。啓林館では602÷3の筆算が例示してあるが、おろすの0についての言及はとくにない。
省略算をつかってどんな場合でも筆算ができる、ということを目指すならば(たとえば4桁÷1桁でvUo[*]型なども考えられる)、おろす→たてる・かけるを次の桁までスキップするこの形も押さえないといけない。
筆算の習熟のイシューは、どこまで完璧を求めるか? である。考え方としてはあらかたの一般型を中心に習熟を図って、特殊型までは全員習熟までは求めない、というやり方も考えられる。しかし指導体系をつくる時には、桁を増やした時にこの特殊形が必要になることも念頭に入れなければならない。
