
応用編〈1〉動かす① すごろく型
さて、応用編です。応用編は、偶然を発生させる装置とは別の装置を操作して、答えを導き出す、という問題です。
別の「装置」を操作して、その状態が判定条件となる、ということになります。偶然を発生させる装置の結果によって、別の装置を操作するので、問題文は複雑になりがちです。読解力が試される問題も見受けられます。

この「別の装置」ごとに分類してみましたので、一つ一つ見てみましょう。一つめはすごろく型の問題です。いわゆる「動点」の問題ですが、動点の問題にも2種類あって、すごろくゲームのように直線上に行ったり来たりするものと、正多角形のような図形の周上をぐるぐる回るものとに更に分類することができます。
すごろくより抽象的な数直線をつかって、その上を点が行ったり来たりする問題もこのすごろく型に分類します。
下の図のように,数直線上に点Pがある。Pは下の〈規則〉にしたがって数直線上を移動する。

〈規則〉
① 1枚の硬貨を1回投げて,表が出たら,右に2だけ移動する。
② 1枚の硬貨を1回投げて,裏が出たら,左に1だけ移動する。
例えば,点Pが0を表す位置にあり,1枚の硬貨を続けて2回投げて,表,表となったとき,P が移動した位置に対応する数は4である。
このとき,次の(1),(2)に答えなさい。ただし,硬貨の表裏の出かたは同様に確からしいとする。(石川県2018)
(1) 点Pは0を表す位置にあり,1枚の硬貨を続けて4回投げたとき,裏,裏,表,裏となった。このとき,Pが移動した位置に対応する数を書きなさい。
(2) 点Pは0を表す位置にあり,1枚の硬貨を続けて3回投げた後,Pが移動した位置に対応する数の絶対値が3になる場合と0になる場合は,どちらが起こりやすいか。
次のア~ウから適切なものを1つ選び,その符号を書きなさい。また,そう判断した理由を説明しなさい。説明においては,図や表,式などを用いてよい。
ア 絶対値が3になる場合の方が起こりやすい。
イ 絶対値が0になる場合の方が起こりやすい。
ウ どちらも起こりやすさは同じである。
硬貨によって「偶然」が発生し、その結果によって「数直線上の点Pを操作」ということになります。
問題文の〈規則〉にしたがって、実際に動かした結果を書き出します。書いて、目で見て次を考える、というクセをつけておいた方がよいです。頭の中ですべて考えようとしない方がいいですよ。
(1)
結果を書き出してみると、次のようになります。
1回目:裏=左に1移動 0 → -1
2回目:裏=左に1移動 -1 → -2
3回目:表=右に2移動 -2 → 0
4回目:裏=左に1移動 0 → -1
(表)×2-(裏)で計算できるかな、というところまで気づくと上級編。
(2)
硬貨を3回投げたとき、起こりうるすべての場合は下の樹形図のように8通りである。それぞれの場合の時のPの位置も図に書き加えておく。
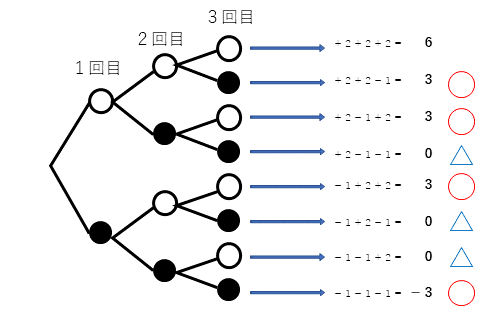
そのうち、絶対値が3になるのは、-3か3のときであり、図の○の場合で、その確率は$${\dfrac{1}{2}}$$。
また、絶対値が0になるのは、図の△の場合で、その確率は$${\dfrac{3}{8}}$$。
絶対値が3になる場合の確率の方が大きいから、絶対値が3になる場合の方が起こりやすい。
答え
(1) -1
(2) ア
上の図から、絶対値が3になる確率は$${\bm{\dfrac{1}{2}}}$$で、絶対値が0になる確率$${\bm{\dfrac{3}{8}}}$$よりも大きいから。
類題・・・
茨城県2023、奈良県2023、埼玉県追試験2022、沖縄県2022、茨城県2021、和歌山県2020、岩手県2019、千葉県2019、石川県2018(例題採集)、沖縄県2017、福井県2016、長崎県2015A・長崎県2015B、福井県2014、宮崎県2014、千葉県2013、奈良県2013、神奈川県2012、愛知県B2012、鹿児島2012、京都府2011、沖縄県2011、富山県2010、滋賀県2010、長崎県A・B2010、福井県2009、山口県2009、沖縄県2008、千葉県2007、神奈川県2007、石川県2007、愛知県B2006、山口県2006、徳島県2006、鳥取県2005、福島県2004、大分県2004、宮崎県2004など
-----------------------
次の問題>
■ 目次 ■
この記事が気に入ったらサポートをしてみませんか?
