
兵庫県|公立高校入試確率問題2024
大小2つのさいころを同時に1回投げ,大きいさいころの出た目の数を$${a}$$,小さいさいころの出た目の数を$${b}$$とする。次の確率を求めなさい。
ただし,さいころの1から6までのどの目が出ることも同様に確からしいとする。
① $${ab}$$の値が奇数となる確率を求めなさい。
② $${ab+3b}$$の値が偶数となる確率を求めなさい。
③ $${a^2-5ab+6b^2}$$の値が3以上の奇数となる確率を求めなさい。
分類:18 【研究】積が奇数・偶数になる確率
融合A3 因数分解・2次方程式
考え方その1 とにかくマス目を埋めて
(1)のその1
偶然は2回起こるので表をかいて考えます。大きいさいころと小さいさいころで同じ目が出ることがありますので,表はいじりません。起こりうるすべての場合は36通り。
各マスに$${ab}$$,つまり大小2つのさいころの目の積を書いて判定してみましょう。
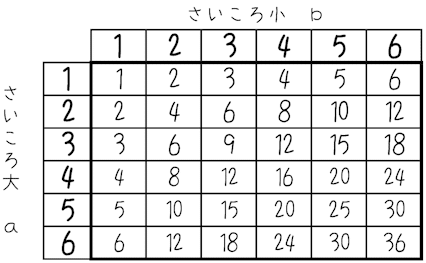
値が奇数になるのは

印をつけた9通りですから,求める確率は$${\dfrac{9}{36}=\dfrac{1}{4}}$$。
(2)のその1
表をつくって,とにかく代入して$${ab+3b}$$の値をそれぞれ求めて表を埋めてみましょう。

このうち,$${ab+3b}$$の値が偶数となるのは

表で印をつけた27通りありますから,求める確率は$${\dfrac{27}{36}=\dfrac{3}{4}}$$。
(3)のその1
表をつくって,とにかく代入して$${a^2-5ab+6b^2}$$の値をそれぞれ求めて,表を埋めてみましょう。

このうち,$${a^2-5ab+6b^2}$$の値をの値が3以上の奇数となる場合は

8通りありますので,その確率は$${\dfrac{8}{36}=\dfrac{2}{9}}$$となります。・・・とサラリと書きましたが,さすがに$${a^2-5ab+6b^2}$$の値を求めるのは大変です。
考え方 その2 偶数・奇数に注目
(1)のその2 積が奇数になるというのは・・・?
(偶数)×(偶数)=(偶数)
(奇数)×(偶数)=(偶数)
(偶数)×(奇数)=(偶数)
(奇数)×(奇数)=(奇数)
積が奇数になるのは,奇数同士をかけたときだけでした。

というわけで,9通り,と考えてもよいです。というか,この考え方を身につけておいた方がいいです。
(2)のその2 和が偶数になるというのは・・・?
(偶数)+(偶数)=(偶数)
(奇数)+(偶数)=(奇数)
(偶数)+(奇数)=(奇数)
(奇数)+(奇数)=(偶数)
という性質を思い返すと
① $${ab}$$が偶数で$${3b}$$も偶数
② $${ab}$$が奇数で$${3b}$$も奇数
のどちらかであればよいわけです。
①は,$${3b}$$のところに着目すると(奇数)×$${b}$$=(偶数)になっていればいいので,$${b}$$は偶数になります。$${b}$$が偶数なので,自動的に$${ab}$$は偶数になり,$${a}$$は何でもよい,ということになります。
つまり,$${b}$$が偶数のところはOKということになります。

①の場合が当てはまるのは18通り。
一方②は,さっきやりましたが,$${a}$$も$${b}$$も両方奇数です。すると,$${3b}$$も奇数ですので,$${ab+3b}$$は偶数になります。

当てはまる場合は(1)で計算したように9通り。
①と②は同時に起こることがありませんから,あわせて27通りです。求める確率は$${\dfrac{27}{36}=\dfrac{3}{4}}$$。
・・・あれ? ちょっとめんどくさいぞ。
(3)のその3
$${a^2}$$と$${-5ab}$$と$${6b^2}$$の和が奇数? しかも3以上? この考え方ではどうもうまくいかなさそうです。かといって,いちいち代入も。
考え方 その3 因数分解できるぞ?
(2)のその3
$${ab+3b}$$を見たら$${b(a+3)}$$と因数分解したくなりませんか? となると,$${b}$$と$${a+3}$$のどちらかが偶数なら,その積も偶数ですね。

ですから当てはまる場合は
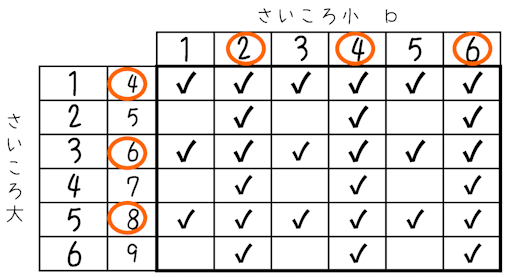
27通り。確率は$${\dfrac{27}{36}=\dfrac{3}{4}}$$。
(3)のその3
因数分解すればよいのだ,という知恵がつきましたので,$${a^2-5ab+6b^2=(a-2b)(a-3b)}$$と因数分解をして,かけ算の答えを表に書いていきましょう。計算のしやすさを考えて,$${2b}$$と$${3b}$$の値をあらかじめ書いておきます。3以上になればいいので,積をいちいち計算する必要はないかもしれませんが,とりあえず計算までした表は次のようになります。

✓印をつけた8通りが該当しますので,確率を求めると$${\dfrac{8}{36}=\dfrac{2}{9}}$$
(3)のその4
・・・とこのように,コツコツとやれば,答えまでたどり着くわけですが,さすがにこれだけ計算をガリガリとやりきるのは大変で,試験の時間ももったいない。もう少し方法はないでしょうか。$${a^2-5ab+6b^2=(a-2b)(a-3b)=(2b-a)(3b-a)}$$が奇数ということは,$${2b-a}$$も$${3b-a}$$も両方奇数,ということですね。
$${2b-a}$$が奇数ということは,$${2b}$$はかならず偶数ですから,$${a}$$は奇数,ということになります。
さらに,$${3b-a}$$が奇数で$${a}$$は奇数ですから,$${3b}$$は偶数で$${b}$$が偶数,ということになります。
いじょうのことから、$${a}$$は奇数でかつ$${b}$$が偶数という条件が導き出されます。
ここまで絞れれば,後は積が3以下になるかどうかをチェックすればよいですね。(問題文をちゃんと読んで,もう一つの条件を忘れずに。出題者はちゃんと落とし穴を掘ってあります)
試験本番,初見でここまで条件を絞れれば上級者,といえるでしょう。兵庫県の確率問題はいつも難しいのですが,今年は,「大小2つのさいころを同時に1回」という見た目いけそうかな,と思わせておいて,なかなか複雑な処理をさせる,難度をうまい具合に調整していいところを突いてくる問題ですね。今後も荒ぶる樹形図問題でないところで勝負していただいければいいのですが。
答
① $${\bm{\dfrac{1}{4}}}$$ ② $${\bm{\dfrac{3}{4}}}$$ ③ $${\bm{\dfrac{2}{9}}}$$
この記事が気に入ったらサポートをしてみませんか?
