
長崎県|公立高校入試統計問題2024
図1は、ある中学校の1年生40人に対して、5月と6月に行った数学の10点満点の小テストの得点の結果をもとにそれぞれ作成したヒストグラムである。このとき、次の(1)~(3)に答えよ。

(1)5月の小テストで、得点が4点以下の生徒は何人か。
(2)5月の小テストの得点と6月の小テストの得点の散らばりの程度(散らばりのぐあい)はどちらが大きいか、5月の小テストのヒストグラムと6月の小テストのヒストグラムから読み取れる数値を比較して説明せよ。
(3)次の①~④について、図1から読み取れることとして、必ず正しいと判断できるものを1つ選び、その番号を書け。
① 最頻値(モード)は、5月の小テストよりも6月の小テストの方が大きい。
② 中央値(メジアン)は、5月の小テストよりも6月の小テストの方が大きい。
③ 5月の小テストの得点が7点以上の生徒のうち、6人が6月の小テストで得点を伸ばした。
④ 5月の小テストの得点よりも6月の小テストの得点が低い生徒が7人以上いる。
(1)
4点以下ですので,4点も含みます。5月の方のヒストグラムを見てみると

0+0+0+3+7=10 で,10人ですね。
(2)
グラフの形をざっくりと見てみましょう。

ここでは度数折れ線をかいていますが,実際にはかくまでもなく,ヒストグラムのなんとなくの形がつかめればよいでしょう。5月と6月の散らばり具合をざっくり見てみると,5月の方が,真ん中らへんにキュッと集まっている感じ,6月の方が左右にだらっと広がっていて,真ん中がちょっとへこんでいる感じ。これを「キュッ」とか「だらっ」とかという感覚的にではなく,問題文にあるように「ヒストグラムから読み取れる数値を比較して説明」すると,例えば下の解答例のように,範囲(最大値と最小値の差)を数字で示すのがよいでしょう。
(3)
1つ1つの選択肢を確認していくことにしましょう。
①最頻値
最頻値は,データの中でもっとも多く現れている値です。ヒストグラムの棒がいちばん高いところになります。

違いますね。この選択肢は誤り。
② 中央値
データの総数は40個ですから,中央値は,データを小さい値から順に並べたときに

【20】番と【21】番の平均値になります。ですから,【20】番や【21】番がどこの階級に属しているかを見てみればよいです。ヒストグラムでは,各階級の度数から累積度数を調べてみるとよいですね。

同じ6点ですから,この選択肢も誤りです。
③ある区間に含まれるデータの数
7点以上の人を見てみましょう。5月で8点取った人が全員9点とったとして,7点だった人が6人8点を取ったとしたら,伸びた人は14人になりますね。ちょうど6人にはなりませんから,この選択肢も誤りです。

④ある区間に含まれるデータの数 その2
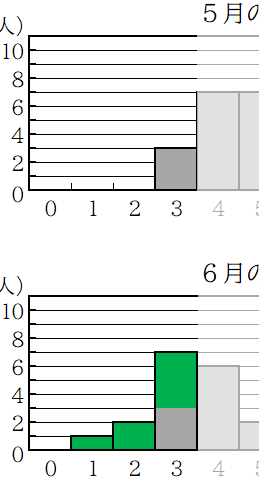
もし5月に3点を取った人が,そのまま3点だったとしても,6月に3点以下を取っている人が7人いますので,この選択肢が正しいと判断できます。
答
(1) 10人
(2)(教育委員会による解答例)
5月の小テストの得点の範囲は5点、6月の小テストの得点の範囲は8点で、6月の小テストの範囲の方が大きいから、6月の小テストの方が得点の散らばりの程度(散らばりのぐあい)が大きい。
(3) ④
この記事が気に入ったらサポートをしてみませんか?
