三重県｜公立高校入試統計問題2023

《１》　下の図はＰ中学校の３年生２５人が投げた紙飛行機の滞空時間について調べ，その度数分布表からヒストグラムをつくったものである。たとえば，滞空時間が２秒以上４秒未満の人は３人いたことがわかる。
　このとき，紙飛行機の滞空時間について，最頻値を求めなさい。

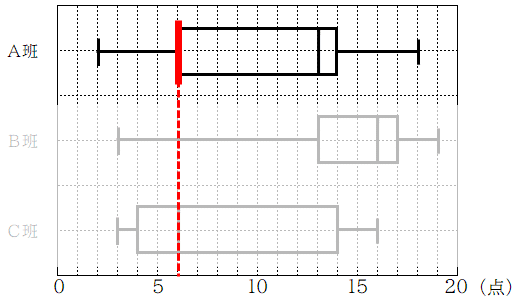
《２》　ひびきさんは，Ａ班８人，Ｂ班８人，Ｃ班１０人が受けた，２０点満点の数学のテスト結果について，図１のように箱ひげ図にまとめた。図２は，ひびきさんが図１の箱ひげ図をつくるのにもとにしたＢ班の数学のテスト結果のデータである。
　このとき，あとの各問いに答えなさい。
　ただし，得点は整数とする。

（１）Ａ班の数学のテスト結果の第１四分位数を求めなさい。

（２）Ｂ班の数学のテスト結果について，$${m}$$，$${n}$$の値をそれぞれ求めなさい。ただし，$${m<n}$$とする。

（３）Ｃ班の数学のテスト結果について，データの値を小さい順に並べると，小さい方から６番目のデータとしてありえる数をすべて答えなさい。

（４）図１，図２から読みとれることとして，次の①，②は，「正しい」，「正しくない」，「図１，図２からはわからない」のどれか，下のア～ウから最も適切なものをそれぞれ１つ選び，その記号を書きなさい。
①Ａ班の数学のテスト結果の範囲（はんい）と，Ｂ班の数学のテスト結果の範囲は，同じである。
〔ア．正しい　イ．正しくない　ウ．図１，図２からはわからない〕
②Ａ班，Ｂ班，Ｃ班のすべてに１４点の人がいる。
〔ア．正しい　イ．正しくない　ウ．図１，図２からはわからない〕

《１》ヒストグラムから最頻値

　最頻値とは，データの中で最も多く出てくる値で，度数分布表やヒストグラムでは，度数の最も多い階級の階級値（階級の真ん中の値）を指します。
　度数の最も多い階級はヒストグラムから４秒以上６秒未満と読み取れますので，その階級値は５秒，ということになります。

《２》（１）箱ひげ図から第１四分位数

　箱ひげ図において，第１四分位数は箱（長方形）の左側の辺で示されます。

　この目盛りを読み取ると６点。

《２》（２）パズル？

　まず答えを書いてしまいます。$${m}$$＝3、$${n}$$ =17。これをどう求めるか。

　まず箱ひげ図から５つのデータを直接読み取れます。
　　　最小値　３
　　　第１四分位数　１３
　　　中央値　１６
　　　第３四分位数　１７
　　　最大値　１９

　最小値と最大値はちょうどその値が含まれていなければなりませんが，最小値の３はないので、$${m}$$，$${n}$$のうち小さい方の$${m}$$の値が３，ということになります。

　次に$${n}$$が，中央値よりも大きいか小さいか、場合に分けて絞っていくことにします。
　中央値よりも大きいとすると，このデータを小さい順に【５】番目まで並べると
　　　3，12，14，15，17
となり，第１四分位数や中央値はあっています。
　ですから、$${n}$$は中央値よりも大きいと考えられます。次に，【５】番目以降となる
　　　17，17，19
のどこに入るかを考えると、第３四分位数が1７ですから，【６】番目と【７】番目のデータの値の平均値が１７，・・・ということは【６】番目と【７】番目のデータでなければなりません。ですから，$${n}$$＝１７であるということがわかります。

　念のため，求めた$${m}$$，$${n}$$を含めて，もう一度小さい値から順にデータを並べてみると，
　　　3，12，14，15，17，17，17，19
　最小値・最大値や四分位数が、箱ひげ図にから読み取れる値と等しいデータになることがわかります。

《２》（３）パズル？　その２

　Ｃ班で小さい方から【６】番目のデータとは，どういう位置づけにあるのかをまずは確認しましょう。
　Ｃ班には１０人いますので，【５】番と【６】番のデータの平均値が中央値で，箱ひげ図から６点であることが変わります。
　いちばんわかりやすいのは【５】番と【６】番ともに６点。これも可能性の一つです。
　あと平均が６点になればいいのと，得点の値は整数だ，というところに気をつければ，５点と７点，４点と８点，３点と９点，２点と１０点，１点と１１点，０点と１２点も考えられます。さらに整数としか書いていないので，マイナスの得点も考えられます‥ と，ちょっと待った。第１四分位数が４点で，【３】番目のデータに当たりますから，【５】番のデータが３点以下になることはありません。
　というわけで【５】番と【６】番の可能性として残るのは、６点と６点，５点と７点，４点と８点の３つです。
　答えは６点，７点，８点となります。

《２》（４）箱ひげ図から読み取れること

　①・②順番に確認していきましょう。

①箱ひげ図と範囲

　範囲とは，最大値から最大値をひいた値です。箱ひげ図では，最小値から最大値までの全体の長さで表されます。

　確かに同じですね。

②ちょうどその値のデータがあるか

　図２から，Ｂ班には１４点の人がいます。
　Ａ班とＣ班の箱ひげ図のちょうど１４点のところはどうなっているでしょうか。

　Ａ班とＣ班はちょうど第３四分位数のところにあります。なので「正しい」・・・というひっかけ問題。Ａ班とＣ班の第３四分位数は，どう求めるのでしょう？
　Ａ班は８人いますから，第３四分位数は，小さい方からデータを並べたときの【６】番目と【７】番目の平均値。

　たとえば１３点と１５点の可能性もあります。そしてその時はちょうど１４点の人はいません。
　でも，【６】番目と【７】番目はどちらも１４点の可能性もあります。
　ですから「正しい」とは言えませんし，かといって「正しくない」とも言い切れません。ということで「図１，図２からはわからない」を選択します。

答

《１》　５秒
《２》　（１）　６点　　（２）　$${m}$$＝3、$${n}$$ =１７
　　　（３）　６，７，８　　（４）　①　ア　　②　ウ

問題を解いた後に

　正直、８とか１０のデータ数どうしで，箱ひげ図で分布を比較って，どういうことさ。《２》の（２）や（３）は，本質的な統計グラフの使い方ではありません。だいたい，タイトルでも書きましたが，数学的な遊び，パズルです。
　箱庭の中で独自の遊びを作れば，それは自己目的化するのであって，統計そのものの理解とは異なる，というのは押さえた上で出題しなければなりません。