
神奈川県追試験|公立高校入試統計問題2024
Kさんは,ある中学校の3年生で,サッカー部に所属している。右の図は,サッカー部に所属する3年生20人それぞれの,サッカーの経験年数をヒストグラムに表したものである。なお,階級はいずれも,1年以上2年未満,2年以上3年未満などのように,階級の幅を1年にとって分けている。
放課後に1人10本ずつ20人全員がシュートの練習を行い,それぞれのシュートの成功した数を記録することになった。

Kさんは,サッカー部の3年生を,経験年数3年未満の生徒と3年以上の生徒の2つのグループに分け,シュートの成功した数を比較することにした。次の資料は,経験年数3年未満の生徒と3年以上の生徒について,それぞれのシュートの成功した数をKさんが調べて記録したものである。
このとき,あとの(i),(ii)に答えなさい。
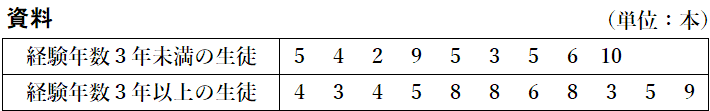
(i) サッカーの経験年数の中央値が含まれる階級として正しいものを次の1~4の中から1つ選び,その番号を答えなさい。
1. 1年以上2年未満
2. 2年以上3年未満
3. 3年以上4年未満
4. 4年以上5年未満
(ii) Kさんは,資料から読み取ったことを次のようにまとめた。(a),(b),(c),(d)にあてはまるものをそれぞれの選択肢の中から1つ選び,その番号を答えなさい。
資料より,シュートの成功した数について,次のことがわかった。
・経験年数3年以上の生徒のほうが,3年未満の生徒よりも[(a)]と[(b)]がどちらも大きい。
・経験年数3年以上の生徒のほうが,3年未満の生徒よりも[(c)]。さらに,[(d)]。
(a)・(b)の選択肢 ※順番はどちらでもよい
ア 平均値 イ 最頻値 ウ 中央値
(c)・(d)の選択肢 ※順番はどちらでもよい
エ 最大値と最小値がどちらも大きい
オ 第1四分位数と第3四分位数がどちらも大きい
カ 成功した数が5本以上の生徒の割合が大きい
キ 成功した数が3本以下の生徒の割合が小さい
(i)ヒストグラムから中央値
中央値は,小さい順にデータを並べたときの【10】番と【11】番の平均の値になります。

ヒストグラムから中央値を求めるには,度数とそこからさらに累積度数を求めていきます。

というわけで,中央値が含まれる区間(階級)は,3年以上4年未満です。
(ii)資料から読み取れること
データから平均値と最頻値と中央値
3つの代表値を求めてみましょう。
平均値 まずそれぞれのデータの合計を求めます。
経験年数3年未満の生徒
$$
\begin{array}{rcl}
(5+4+2+9+5+3+5+6+10) \div 9 & = & 49 \div 9 \\
& = &5.44444..
\end{array}
$$
経験年数3年以上の生徒
$$
\begin{array}{rcl}
(4+3+4+5+8+8+6+8+3+5+9) \div 11 & = & 63 \div 11\\\\
& = &5.727272..
\end{array}
$$
最頻値

3年未満は5本、3年以上は8本ですね。
中央値 データを小さい値から順に並べます。

中央値は両方とも5ですね。
ですから,ここで選ぶのは平均値と最頻値。
最小値と最大値
最小値は2本と3本で3年以上の方が大きいが,最大値は10本と9本で、3年未満の方が大きいので,この選択肢は正しくない。

第1四分位数と第3四分位数
さっき中央値を求めるときに,データの値が小さい順に並べてありますので,それを活用して四分位数を求めると,
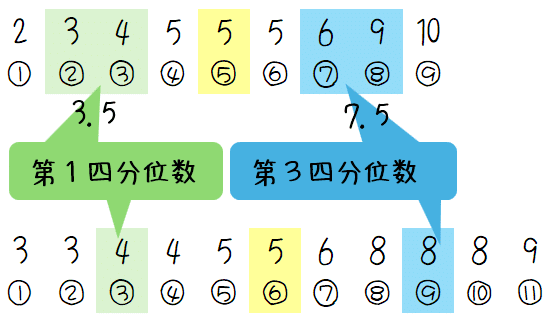
確かに、3年以上の生徒の方の第1四分位数と第3四分位数がどちらも大きいです。
5本以上の生徒の割合

5本以上の生徒は,経験年数3年未満の生徒で6人、経験年数3年以上の生徒で7人います。
6÷9=0.66666.…
7÷11=0.6363636.…
成功した数が5本以上の生徒の割合は,経験年数3年未満の生徒の方が大きい。
3本以下の生徒の割合

3本以下の生徒は,経験年数3年未満・経験年数3年以上の生徒ともに2人います。割合は
2÷9=0.222222.…
2÷11=0.181818181.…
こちらは,確かに成功した数が3本以下の生徒の割合は,経験年数3年以上の生徒の方が大きいです。
答
(i) 3
(ii) a・b ア,イ c・d オ,キ
