
融合問題編《B2》円周角
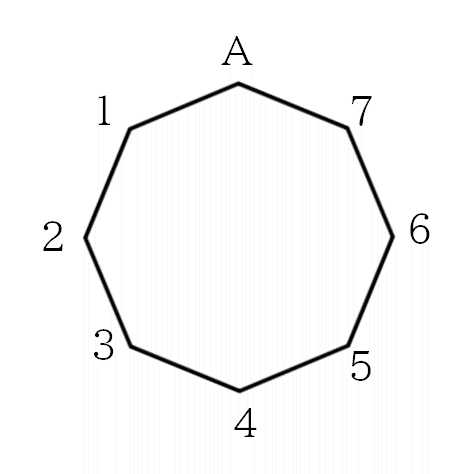
右の図のような正八角形があり,1つの頂点にはAが,他の7つの頂点には、1から7までの番号がふられている。1から7までの数字が1つずつ書かれた7枚のカード1,2,3,4,5,6,7から2枚のカードを取り出し,カードに書かれた数字と同じ番号の2点と,点Aの3点を結んで,これらの3点を頂点とする三角形をつくる。このとき,その三角形が直角三角形となる確率を求めよ。
ただし、どのカードが取り出されることも同様に確からしいものとする。(愛媛県2012)
表を書いて分母を決める
どんな偶然が起こっているかをまずつかんでおきましょう。1~7から2枚のカードを同時にひく表を書いておきます。
分子:図形の知識・・・
次に,円周上の3点が直角三角形になるのは、三角形のうちの1辺が円の直径になっている場合です。(何言っているかよく分からない場合は、ここのnoteでは確率の融合問題としてこんなのが出るよ、ということなので,円周角の学習をしておきましょう)
というわけで,「Aと4と何か」を選んだ場合はAと4で直径になるのと,A以外の2点(1と5,2と6,3と7)が直径になる場合,ということで,表はこのようになるので,求める確率は
$${\dfrac{9}{21}=\dfrac{3}{7}}$$
類題:長崎県B2020、神奈川県2016、島根県2016、長野県2011
この記事が気に入ったらサポートをしてみませんか?
