基礎編３０.５＊　「２つ取り出すの分母⑤」【研究】取り出して，戻さずもう１回。だけど取り出す順序は実は関係ない

　箱の中に１，２，３，４，５と書かれたカードが１枚ずつ，合計５枚入っている。この箱から１枚のカードを取り出し，箱にもどさずにもう１枚のカードを取り出す。
　このとき，取り出した２枚のカードに書かれている数が，どちらも奇数である確率を求めよ。ただし，それぞれのカードの取り出し方は同様に確からしいとする。（福井県2005）

問題を解く前に・・・

　問題の構造としては基礎編14と同じです。まずは基礎編14と同じように解いてみましょう。

分母は・・・

　例によって１枚目は「Ａさん」に、２枚目は「Ｂさん」にひいてもらいます。１枚目のＡさんにとっての「１をひく」「２をひく」「３をひく」「４をひく」「５をひく」の5通り。２枚目をひくＢさんにとっても，「１をひく」「２をひく」「３をひく」「４をひく」「５をひく」の５通り。

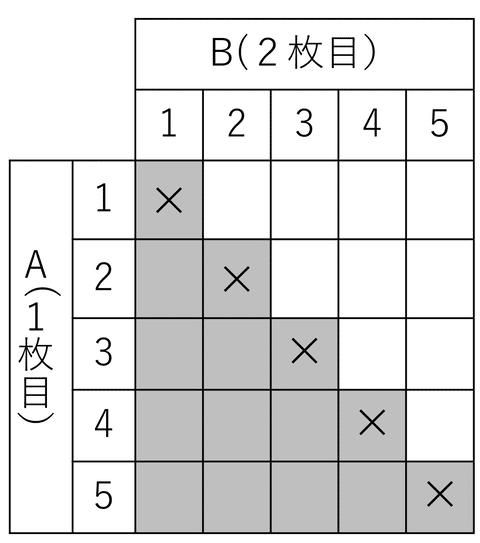
　「取り出して戻さない」ので、基礎編14と同じように対角線に×をつけておきましょう。２人のとり出し方はＡ→Ｂの順序がありますので、Ｃ型ではなくＰ型。左下は残しておきます。

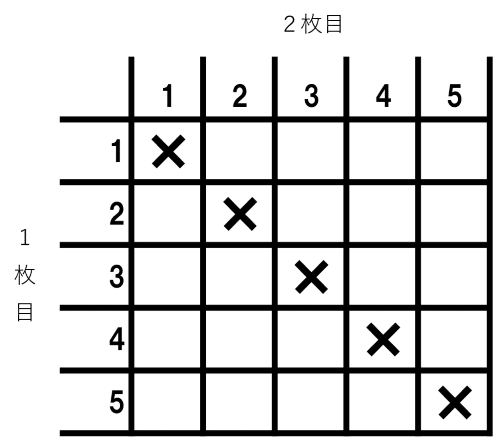
　表の中で×のついていないマスを数えると，２０通り。この２０通りが、同様に確からしく起こることがら、ということになります。

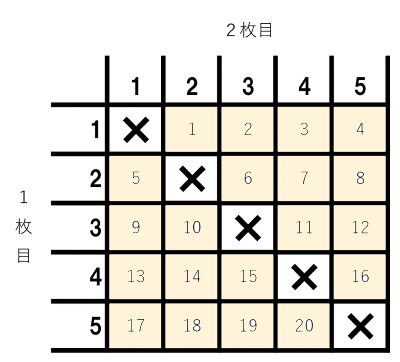
分子は・・・

　取り出した２枚のカードに書かれている数が，どちらも奇数である確率は、表のように６通り。

　ですから、確率を求めると　$${\dfrac{6}{20}=\bm{\dfrac{3}{10}}}$$　となります。

答えは・・・

$${\bm{\dfrac{3}{10}}}$$

【研究】でも実は、取り出す順序は・・・

　ここまでオーソドックスに解いてきましたが、上で書いた「２人のとり出し方はＡ→Ｂの順序がありますので、Ｃ型ではなくＰ型」という説明、実はＣ型でもいいのですよ、というのがこの【研究】です。
　だって、Ａ→Ｂって取り出したとしても、Ｂ→Ａって取り出したとしても、「どちらも奇数であるかどうか」を判定するのには影響しないですよね。ということなんです。
　順序が関係ない・・・ということは，この問題は基礎編１５のようにＣ型で考えてもよいのです。Ｃ型で考えると、表は

のようになります。全ての場合は１５通り。奇数になるのは表のように、３通り。

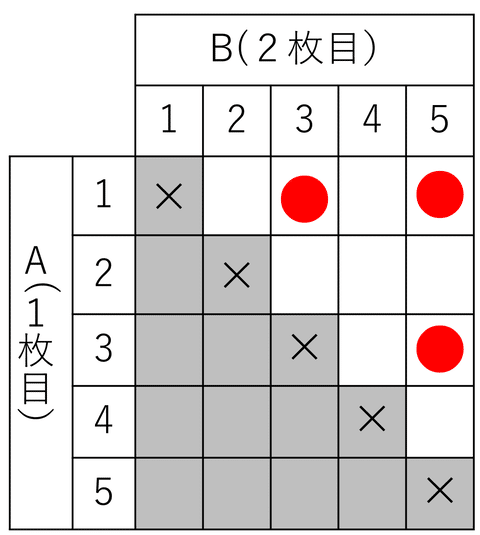
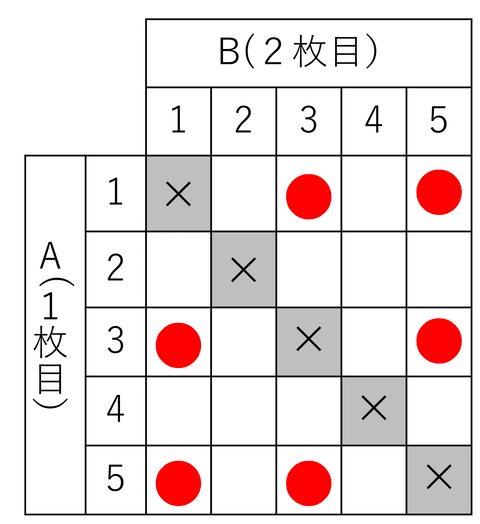
ですからその確率は、$${\bm{\dfrac{3}{10}}}$$。先ほどＰ型で求めた確率と同じになります。Ｐ型の表とＣ型の表を並べてみましょう。×をつけた対角線と対象に●印がついてるのがわかるでしょうか。表の右上と左下は同じパターンが生じるので、２でわったのがＣ型、ということになります。

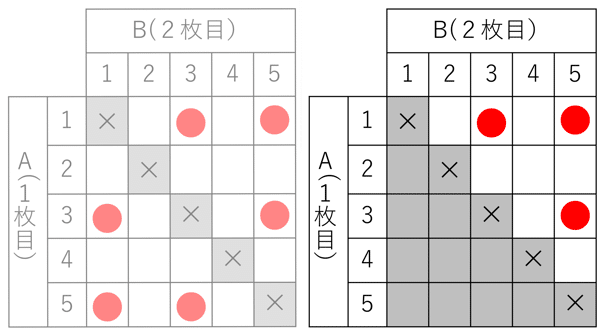
　順番に取り出すけれども，分子判定のときには、取り出した順番はどうでもいい、というときも，はじめからＣ型で考えてよい、ということになります。「取り出し方」だけではなく、取り出した後の条件にも目を配っておいた方がよい，ということですね。
　このようにあらかじめ考えておくことは、計算が簡単になるだけではなく、「どうせ同じことが起こるので，最初からわっておいて考える」という考え方は、高校に入ってからとても重要になります。

－－－－－－－－－－－－－－－－－－－－－－－
＜前の問題　　　　　次の問題＞
問題一覧

※23.2.19　基礎編30.5のカテゴリーを新設して、もと［基礎編14］として採録していた例題をこの項に移動。（基礎編14の問題は新しいものに差し替え）