秋田県Ⅱ｜公立高校入試確率問題2018

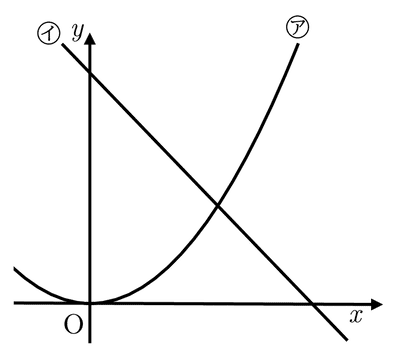
　右の図において，㋐は関数$${y=\dfrac{1}{4}x^2}$$，㋑は関数$${y=-x+b}$$のグラフである。
　大小２つのさいころを同時に１回投げたとき，大きいさいころの出た目の数を$${m}$$，小さいさいころの出た目の数を$${n}$$とし，２つのさいころを投げたときにできる点の座標を（$${m, n}$$）とする。
　次の①・②の問いに答えなさい。ただし，さいころのどの目が出ることも同様に確からしいものとする。（改題※）

① 　㋑において$${b}$$=6のとき、点（$${m,n}$$)が、$${y}$$軸と㋐，㋑の$${x≧0}$$の部分で囲まれた図形の内部にある確率を求めなさい。ただし，$${y}$$軸と㋐，㋑の$${x≧0}$$の部分で囲まれた図形の周上の点も内部に含まれるものとする。

②　点（$${m, n}$$）が，$${y}$$軸と㋐，㋑の$${x≧0}$$の部分で囲まれた図形の内部にある確率が$${\dfrac{1}{2}}$$であるとき，$${b}$$のとりうる値の範囲を求めなさい。ただし、$${y}$$軸と㋐，㋑の$${x≧0}$$の部分で囲まれた図形の周上の点も内部に含まれるものとする。

分類：融合《Ｃ３》座標・関数-放物線・双曲線

さいころ２つなので表！で、勢いで解いてみる

　まずは表を書いてみます。

　しかし、今回は座標平面上の座標を扱うので，これだと頭が混乱する危険があります。表を座標平面と合わせておいた方がいいかもしれません。

　さて、上下を直線・曲線ではさまれますので、$${x}$$=1のとき$${\dfrac{1}{4}x^2}$$の値と$${-x+6}$$の値を求めて，その間にある$${y}$$の値は？　$${x}$$=2のときはどうか？　・・・　と順番に求めてチェックをしていきましょう。

　すると、条件を満たすのは，上の○・◎（周上にある）の場合ですので、10通り。確率は$${\dfrac{10}{36}=\bm{\dfrac{5}{18}}}$$ということになります。

②も同じように・・・・？

　①を求めるときにわかるように、幸い、$${x}$$=5と$${x}$$=6のときは，下限となるべき$${y=\dfrac{1}{4}x^2}$$の値が6を超えますので、$${b}$$の値が何であっても、$${x}$$=5と$${x}$$=6のときは条件を満たす$${y}$$の値がないことはわかります。

　あとは$${b}$$の値が決め手になりますが、①で見たように、b=6のときは確率は$${\dfrac{1}{2}}$$より小さいです。より面積を大きくして、この図形の中野展を増やすためには、$${b}$$を大きくした方がよいことはわかるでしょう。どこまで大きくすればよいでしょうか。$${b}$$=7,8,9,…と代入して考えてみましょう。条件は、図形にふくまれる場合の数が１８ちょうどになればよい，ということです。

　$${b}$$=9のとき、ちょうど（3，6）と（4，5）が直線$${y=-x+10}$$上にあって図形内部に含まれることになるので、確率が$${\dfrac{1}{2}}$$になります。
　$${b}$$=10になると、ちょうど（4，6）が$${y=-x+10}$$の直線上に入ってきて、確率が$${\dfrac{1}{2}}$$ではなくなります。なので$${b}$$を増やしていくと、$${b}$$＝9から条件を満たし、$${b}$$＝10になるタイミングでNGになります。$${b}$$の取り得る範囲は9≦$${\bm{b}}$$<10ということになります。不等号≦と＜の違いに注意してください。繰り返しになりますが、$${b}$$=9の場合はOKで、$${b}$$＝10の場合は範囲には含まれません。

答

①　$${\bm{\dfrac{5}{18}}}$$　　　②　9≦$${\bm{b}}$$<10

問題を解いたあとに・・・

　ここに採録したのはⅠかⅡの選択問題で、Ⅱは「できる」学校を受ける人が解く想定の問題です。そういう意味では，歯ごたえのある問題ですし、上を目指す人はぜひ触れておいて損はない問題です。

　さて、この問題に受験生が触れたとき，どうしたらいいのか、考えてみましょう。マス目のある座標平面は問題文に含まれていません。
　座標平面を書いて考えたくなるのは確かですし、具体的なイメージをもって解き進めるためには大切です。しかし、実際に点を数えるために図中に格子を書くのは、直線㋑が$${b}$$によって動くことを考えると、コワいです。
　図の上で試行錯誤することは大切ですが，この問題で言うと、自分で０から「数えるための図」をつくり直す必要があります。ただし「キレイな格子」をつくらないと、この作戦で答を出すのは難しいです。格子がないのに０から図をかくのは，受験生にとっては時間を浪費する作業であり、また正確にかけないとすると危険でしかありません。
　というわけで、説明としては、表と場合分けの折衷的な感じになりましたが、たぶん、ｘ＝１のとき、ｘ＝２のとき・・・で６つの場合で、条件に合うｙやｂの値を割り出していく、ということになると思います。（ネット上の各種解説サイトや解説動画を見ると、図式化されて示されています。もちろん具体的なイメージは重要ですが、実際に受験生が紙とエンピツで試行錯誤することがあまり考慮されていない印象があり、頭がいい人や図がきれいに書ける人の解き方ではなく、紙とエンピツと脳内イメージでどれだけ試含めて含めて迫るか！　というのが実際にはもうちょっと充実して書かないといけないかな、.と思っているところです。）