
大学入学共通テスト 2024 本試|大学入試問題なのに中学確率で解ける問題
分類:28 【研究】少なくとも1つ起こる確率
箱の中に[A],[B]のカードが1枚ずつ全部で2枚入っている。この箱の中からカードを1枚取り出し,書かれているアルファベットを確認してからもとに戻すという試行を繰り返し行う。
(1) 2回繰り返すとき,[A],[B]のそれぞれが少なくとも1回は取り出される確率は[ア]/[イ]である。
(2) 3回繰り返すとき,[A],[B]のそれぞれが少なくとも1回は取り出される確率は[ウ]/2^3である。
(3) 4回繰り返すとき,[A],[B]のそれぞれが少なくとも1回は取り出される確率は[エ]/[オ]である。(改題)
樹形図で考えていきましょう
4回まで繰り返すということは偶然も4回起こるところまで考えるので,最初から樹形図で考えることにします。
まず、2回取り出す場合ですが、[A]と[B]のそれぞれが少なくとも1回は取り出される場合は,図から2通り。起こりうるすべての場合は4通りですので,求める確率は$${\dfrac{2}{4}=\dfrac{1}{2}}$$。

「少なくとも1」とは?
[A]と[B]のそれぞれが少なくとも1回は取り出される・・・気が付きましたか? 少なくとも1は「じゃない方を考えるサイン」でしたね。
”[A]と[B]のそれぞれが少なくとも1回は取り出される”じゃない,とは,「[A]か[B]のどちらか1種類しか出ない」ということです。
これを踏まえて3回繰り返すときの樹形図をかきましょう。

このように[A]と[B]のそれぞれが少なくとも1回は取り出される場合をちまちま考えてもいいですが,「[A]か[B]のどちらか1種類しか出ない」という場合を考えれば,[A]1種類しか出ない か [B]1種類しか出ない の2通りです。起こりうるすべての場合は8通りですから,「[A]か[B]のどちらか1種類しか出ない」確率は$${\dfrac{2}{8}=\dfrac{1}{4}}$$。というわけで,求める確率は$${1-\dfrac{1}{4}=\dfrac{3}{4}}$$ということになります。
さあ,4回繰り返すとき,樹形図を気合い入れてかくと
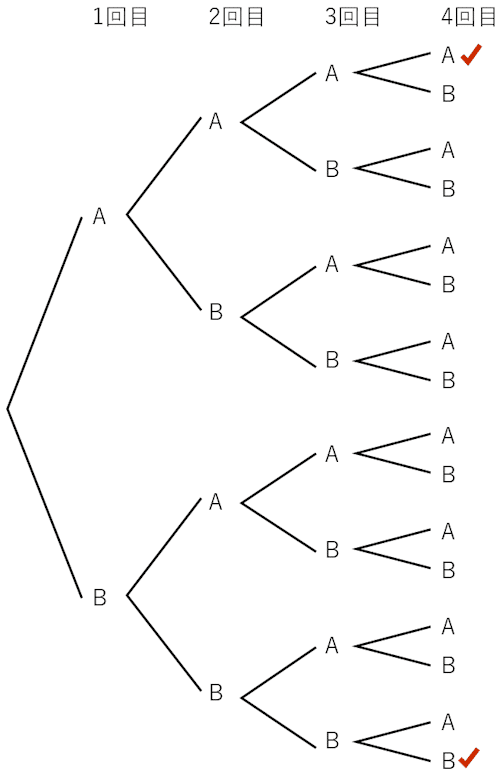
の通り。「じゃない方」は2通りですので,「じゃない方」が起こる確率は$${\dfrac{2}{16}=\dfrac{1}{8}}$$です。求める確率は$${1-\dfrac{1}{8}=\dfrac{7}{8}}$$
答
(1)$${\bm{\dfrac{1}{2}}}$$ (2)$${\bm{\dfrac{3}{4}}}$$ (3)$${\bm{\dfrac{7}{8}}}$$
でも共テ問題文はこねくり回しているので、この通り8点もらえるわけでもない。
ここまで見てなーんだカンタンじゃん,と思った方。残念。上の問題文は中学生用に「翻訳」した文章なのです。多くの中学生は,元の問題を読んだら,たぶんなんのこっちゃ,という感じだと思います。
---------------------
この記事が気に入ったらサポートをしてみませんか?
