
香川県|公立高校入試確率問題2014
表は白色,裏は灰色のカードが6枚あり,それぞれのカードには表と裏に同じ数字が1から6まで書かれている。右の図1は,1と書かれたカードを示している。
この6枚のカードが,右の図2のようにすべて表が上を向いている状態から,1から6までのどの目が出ることも同様に確からしい大小2個のさいころを用いて,次のルールにしたがってカードをひっくり返す。

【ルール】
1回目の操作 大きいさいころを1回投げ出た目の数以上の数字が書かれたカードをすべてひっくり返す。
2回目の操作 1回目の操作後の状態から,小さいさいころを1回投げ,出た目の数以下の数字が書かれたカードをすべてひっくり返す。
たとえば,大きいさいころ,図3の出た目の数が4のとき,1回目の操作後は右の図3のようになり,小さいさいころの出た目の数が5のとき,2回目の操作後は右の図4のようになり,表が上を向いてるカードは2枚となる。

これについて,次のア,イの問いに答えよ。
ア 図2の状態から始めて,このルールにしたがってカードをひっくり返す。大きいさいころの出た目の数が4のとき,2回目の操作後に,表が上を向いているカードが3枚になった。このとき,小さいさいころの出た目の数は何か。
イ 図2の状態から始めて,このルールにしたがってカードをひっくり返す。2回目の操作後に,表が上を向いているカードが1枚になる確率を求めよ。
分類:応用〈3〉 裏返す
アは、実際にやってみよう。
大きいさいころの出た目の数が4のとき,問題文にある例のように1回目の操作で図3の状態になっています。
ここから、小さいさいころで何の目が出るとどうなるか、一つ人考えてみましょう。
●小さいさいころの出た目の数が1のとき
1以下の数字が書かれたカードをすべて、つまり1のカードだけをひっくり返すので、■□□■■■→表が上を向いているカードが2枚で×
●小さいさいころの出た目の数が2のとき
2以下の数字が書かれたカードをすべて、つまり1と2のカードをひっくり返すので、■■□■■■→表が上を向いているカードが1枚で×
●小さいさいころの出た目の数が3のとき
3以下の数字が書かれたカードをすべて、つまり1,2,3のカードをひっくり返すので、■■■■■■→表が上を向いているカードが0枚で×
●小さいさいころの出た目の数が4のとき
4以下の数字が書かれたカードをすべて、つまり1,2,3,4のカードをひっくり返すので、■■■□■■→表が上を向いているカードが1枚で×
●小さいさいころの出た目の数が5のとき
5以下の数字が書かれたカードをすべて、つまり1,2,3,4,5のカードをひっくり返すので、■■■□□■→表が上を向いているカードが2枚で×
●小さいさいころの出た目の数が6のとき
1以下の数字が書かれたカードをすべて、つまり1~6のカード全部をひっくり返すので、■■■□□□→表が上を向いているカードが3枚でOK
ですから、答えは6ということになります。
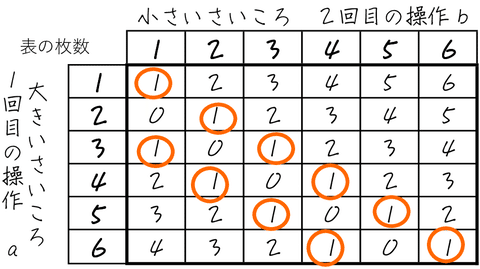
イも表をかいてやってみよう。

この表から、上を向いているカードが1枚なのは、(大きいさいころの目の数,小さいさいころの目の数)の形で表すと、(1,1),(2,2),(3,1),(3,3),(4,2),(4,4),(5,3),(5,5),(6,4),(6,6)の10通り。
ですから、確率を求めると$${\dfrac{10}{36}=\bm{\dfrac{5}{18}}}$$
答
ア 6 イ $${\bm{\dfrac{5}{18}}}$$
表が上を向いているカードを計算で求める方法はないか?
ここからは、研究編。表をかかないで求める方法を考えてみましょう。大きいさいころで出た目の数を$${a}$$,小さいさいころで出た目の数を$${b}$$として考えます。
(1)$${a}$$-1=$${b}$$($${a-b}$$=1)のとき
すべて裏返ります。この状態を境目に考えます。
(2)$${a}$$-1<$${b}$$($${a-b}$$<1)のとき
例えば、問題文のアの状態は$${a}$$=4,$${b}$$=5ですから$${a}$$-1<$${b}$$で、ここにあてはまります。
1回目の操作で$${a}$$~6が裏返り、2回目の操作で1~$${b}$$が裏返ります。$${a}$$~$${b}$$の間が2回裏返って結局表が上を向いています。表が上を向いているカードの枚数は$${b-a+1}$$枚です。
(3)$${a}$$-1>$${b}$$($${a-b}$$>1)のとき
1回目の操作で$${a}$$~6の$${7-a}$$枚が裏返ります。2回目の操作で1~$${b}$$の$${b}$$枚が裏返ります。このとき、2回裏返るカードはありませんので、裏返っている枚数は$${7-a+b}$$枚で、表が上を向いているカードの枚数は$${6-(7-a+b)}$$より$${a-b-1}$$枚です。
結局この3つの場合ともに、表が上を向いているカードの枚数を、($${a-b-1}$$の絶対値)枚である、とあらわすことができます。
アの問題は、4-$${b}$$-1の絶対値が3である、ということですので、3-$${b}$$が+3か-3である、ということになります。
●3-$${b}$$=3のとき $${b}$$=0で、答えとしては適しません。
●3-$${b}$$=-3のとき $${b}$$=6。
イの問題も、$${a-b-1}$$の絶対値が1であるとき、ということになりますので、$${a-b-1=1}$$または$${a-b-1=-1}$$のときの($${a,b}$$)の組をそれぞれ求めることになります。
●$${a-b-1=1}$$のとき
すなわち$${a-b=2}$$のときですので、$${a}$$が$${b}$$より2大きい場合、すなわち(3,1),(4,2),(5,3),(6,4)の4通りの場合があてはまります。
●$${a-b-1=-1}$$のとき
すなわち$${a=b}$$、$${a}$$と$${b}$$が等しい場合ということですので、(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)の6通りの場合があてはまります。
この記事が気に入ったらサポートをしてみませんか?
