
熊本県(A・B共通)|公立高校入試統計問題2023
次の図は,美咲(みさき)さんが通う高校の,1年1組39人と1年2組39人の反復横とびの回数の測定結果を,体育委員である美咲さんが箱ひげ図に表したものである。
このとき,次の各問いに答えなさい。

(1)次の[ア],[イ]に当てはまる数を入れて,文を完成しなさい。
図の1組の箱ひげ図から,回数の範囲は[ ア ]回,四分位範囲は[ イ ]回であることがわかる。
さらに美咲さんは,その測定結果をヒストグラムに表した。
(2) 次のア~エのヒストグラムのうち,1組と2組を表しているものはどれか。それぞれ記号で答えなさい。
なお,ヒストグラムの階級は,40回以上44回未満,44回以上48回未満などのように,階級の幅を4回として分けている。

(3)美咲さんと同じ体育委員の大輔(だいすけ)さん,由衣(ゆい)さん,雄太(ゆうた)さん,恵子(けいこ)さんは,箱ひげ図やヒストグラムから読み取れることについて,それぞれ次のように考えた。
大輔さん:回数の範囲は,1組よりも2組の方が大きい。
由衣さん:回数の四分位範囲は,1組よりも2組の方が大きい。
雄太さん:回数が64回以上である人数は,1組よりも2組の方が多い。
恵子さん:1組の回数の平均値は,60回である。
4人のうち,正しい読み取りをしているのはだれか。次のア~エからすべて選び,記号で答えなさい。
ア 大輔さん イ 由衣さん ウ 雄太さん エ 恵子さん
(1)範囲と四分位範囲
範囲とは,最大値と最小値の差,四分位範囲とは第3四分位数と第1四分位数の差です。それぞれ箱ひげ図から読み取って計算すると,

範囲は28回(暗算するときに繰り下がりに注意!),四分位範囲は9回です。
(2)ヒストグラムと箱ひげ図
箱ひげ図に対応するヒストグラムを探します。まず最小値に注目すると,1組は40回以上44回未満の階級に含まれていて,2組は44回以上48回未満の階級に含まれています。対応するヒストグラムは1組はアかウのどちらかで,2組はイかエのどちらか,ということになります。
最大値は両方とも68回以上72回未満の階級に含まれますから,ウはないことがわかります。1組はアであることが確定します。
では2組はどちらでしょう? 箱ひげ図から,第1四分位数が51回で,48回以上52回未満の階級に含まれます。同様に第2四分位数(中央値)は56回以上60回未満の階級,第3四分位数は64回以上68回未満の階級にそれぞれ含まれます。
データの個数は39個ですから,データを小さい順に並べたときに四分位数がどのデータに対応するか考えてみます。
では,イとエのヒストグラムで【10】・【20】・【30】番目のデータがどの階級に含まれるか,累積度数を求めてみましょう。
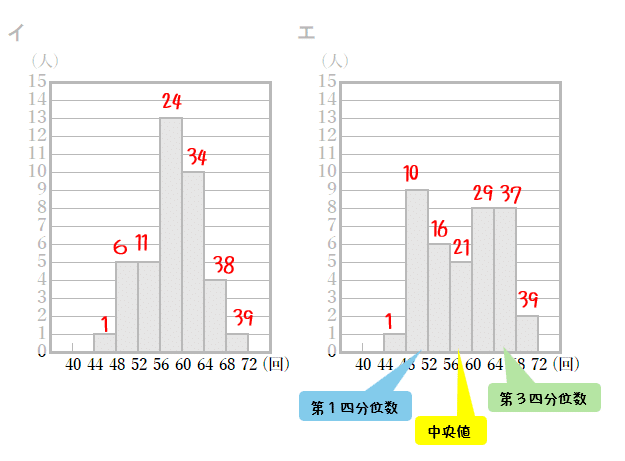
あっているのはエの方のヒストグラムです。
(3)箱ひげ図やヒストグラムから読み取れること
ア 範囲
範囲とは,最大値と最小値の差のことで,箱ひげ図では左のひげの左端から右のひげの右端までの長さで表されます。
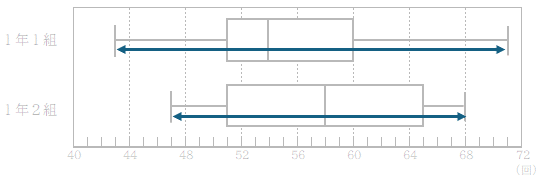
2組の方が小さいですから,この選択肢は間違いです。
イ 四分位範囲
範囲とは,第3四分位数と第1四分位数の差のことで,箱ひげ図では箱(長方形)の上下の辺の長さで表されます。

確かに2組の方が大きいですから,この選択肢は正しいです。
ウ ある区間に含まれるデータの個数
箱ひげ図では,ひげや箱の長さは,データの個数とは関係がありません。そして,四分位数・最小値・最大値の間に「データがある」ことしか示されません。2つの組の違いは,第3四分位数を含んでいるかどうかのところにありそうです。

(2)のところで,2組とも,第3四分位数は小さい順にデータを並べたときのちょうど【30】番目のデータであることがわかっていますので,このデータを含むかどうか,ということはわかります。
それで2組の方が確実に多い,ということがわかるのです。この選択肢は正しい。
エ 平均値
箱ひげ図からは平均値は読み取れません。
ヒストグラムを見てみましょう。
それぞれの階級に属する度数を数えて,階級値を求めて,計算して・・・でもいいのですが,グラフはざっくりと判断するためにかくものです。ざっくり平均値を判断するための方法は,60回のところに次のように「てんびん」の「支点」を置いてみます。そう,支点・力点・作用点の支点です。

どうでしょう? 左側にガクンとなりそうですね。釣り合う点,つまり平均値は60分よりも小さいところにありそうです。ですから,この選択肢は間違いと判定して,次の問題に時間を費やした方がよいでしょうね。こんな直観的な解き方でいいんですか? といわれそうですが,時間があったら,確かめてみましょう。
答
(1) ア 28 イ 9
(2) 1組 ア 2組 エ
(3) イ,ウ
時間があったらの平均値確かめ
1組のヒストグラムはアでしたね。ヒストグラムから度数を読み取ります。
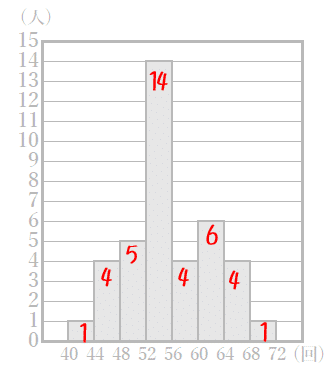
それぞれの階級に属するデータがすべて階級値(階級の真ん中の値)であるとして計算するのでした。

2170÷39=55.6… となります。
こうやって求めた平均値は,「であるとして」計算したもので,もとのデータから計算した「真の」平均値とはズレがあると考えられます。
ただ,さすがに階級の幅の4回以上ずれるということはないだろう,と判断できます。
これだけの計算を費やすぐらいなら,直観で判断してほかの問題に時間を振り分けた方がいい,というわけです。
この記事が気に入ったらサポートをしてみませんか?
