
愛媛県|公立高校入試統計問題2023
ある中学校の,1組,2組,3組で数学のテストを行った。
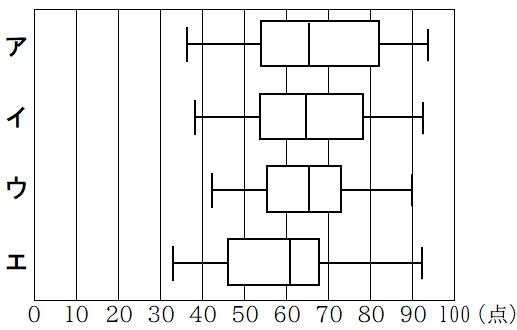
(1) 右の図1は,1組30人の結果をヒストグラムに表したものである。このヒストグラムでは,例えば,40点以上50点未満の生徒が5人いることがわかる。また,下のア~エの箱ひげ図には,1組30人の結果を表したものが1つ含まれている。ア~エのうち,1組30人の結果を表した箱ひげ図として,最も適当なものを1つ選び,その記号を書け。

(2) 次の図2は,2組と3組それぞれ30人の結果を箱ひげ図に表したものである。この箱ひげ図から読みとれることとして,あとの①,②は,「ア 正しい」「イ 正しくない」「ウ この箱ひげ図からはわからない」のどれか。ア〜ウのうち,最も適当なものをそれぞれ1つ選び,その記号を書け。
① 四分位範囲は,3組より2組の方が大きい。
② 点数が45点以下の生徒は,3組より2組の方が多い。

(1)ヒストグラムから箱ひげ図
ヒストグラムは、各階級にどれだけのデータが含まれているかがわかります。また、箱ひげ図はデータを小さい順に並べて、両端と約25%の区切りがどこにあるかがわかります。
2つの図を対応させるには,まずヒストグラムから最大値と最小値がある階級を確かめてみるとよいでしょう。ヒストグラムから、最小値は30点以上40点未満であることがわかりますが,ヒストグラムのウはそうなっていませんので,除外ということになります。残りの3つから、正解を探します。
次にヒストグラムから累積度数を求めるのと,四分位数が小さい順に並べて何番目のデータに対応するかを調べておきます。



第1四分位数が【8】,中央値が【15】と【16】の平均、第3四分位数が【23】のデータに対応していますので,そのデータがある階級をヒストグラムから見つけます。
すると,第1四分位数は50点以上60点未満,中央値は60点以上70点未満,第3四分位数は70点以上80点未満の区間にそれぞれありますから,

これを満たしている箱ひげ図はイ、ということになります。
(2)
箱ひげ図から四分位範囲
四分位範囲とは第3四分位数と第1四分位数の差で,箱ひげ図では箱(長方形)の長さで表されます。

確かに3組の方が長いですから,この選択肢は正しいです。
区間に含まれるデータの個数
箱ひげ図で,45点以下のデータが含まれる区間は

両方とも最小値から、第1四分位数の途中までということだけわかります。2組の方が線が長いので,多くのデータが含まれていると勘違いしそうですが,あくまで,この線のどこかにデータがいくつか,全体の1/4よりも少ない分だけあるということしか表していませんので,ウの「この箱ひげ図からはわからない」を選ぶことになります。
答
(1) イ (2) ① イ ② ウ
