
熊本県B|公立高校入試確率問題2018
下の図1のように,1,2,3の数字が1つずつ書かれた3個の赤玉と1,3の数字が1つずつ書かれた2個の白玉が入った袋がある。また,下の図2のように,点A,B,C,Dを頂点とする正方形がある。点Pは最初,正方形の頂点Aの位置にあり,次の操作を2回続けて行い,Pを移動させる。
〈操作〉
袋の中から玉を1個取り出す。
・玉の色が赤色のときは,Pを時計の針の回転と同じ向きに,玉に書かれた数だけ頂点から頂点へ正方形の辺上を移動させる。
・玉の色が白色のときは,Pを時計の針の回転と反対の向きに,玉に書かれた数だけ頂点から頂点へ正方形の辺上を移動させる。
Pを移動させた後,玉を袋の中にもどす。
例えば,1回目に2の数字が書かれた赤玉を取り出し,2回目に3の数字が書かれた白玉を取り出したとき,Pの最後の位置はBである。

① 1回目に1の数字が書かれた白玉を取り出し,2回目に2の数字が書かれた赤玉を取り出したとき,Pの最後の位置を求めなさい。
② 次の[ ア ]にはA,B,C,Dのいずれかを,[ イ ]には数を入れて,文を完成しなさい。ただし,どの玉が取り出されることも同様に確からしいものとする。
2回の操作のあと,Pの最後の位置となる確率が最も高い頂点は[ ア ]で,その確率は[ イ ]である。
分類:応用〈2〉 動かす② 循環型
①は、ゆっくり考えます。
1回目、1の数字が書かれた白玉なので反時計回りに1つ動いてPはBのいちに,そして2回目に2の数字が書かれた赤玉なのでそこから時計回りに2つ動きます。PはDの位置に動くのですね。
②は表をかいてみるけど・・・?
どんな表をかいて考えましょうか。ここでは、1回目の取り出した玉の結果によってまずPがどこにいるかを書いておいて、次を考えることにします。
すると、「赤の1」「白の3」が出たときは同じDの位置にあります。「赤の3」[白の1」が出たときには同じBの位置にあります。そして,どこからスタートしても2回目に「赤の3」と「白の1」は結局同じ位置にあることがわかります。そうすると、表を埋めるのも同じことを書けばよいので、楽になります。
というわけで、表の各枠には2回目の結果を埋めていくことにしましょう。
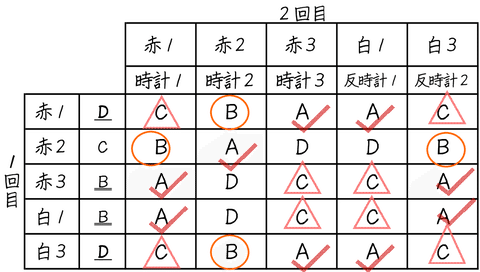
でき上がった表を見ると、
A→9通り
B→4通り
C→8通り
D→4通り
最終的にAに止まっていることが多く、その場合の数は9通り、したがって求める確率も$${\bm{\dfrac{9}{25}}}$$となります。
答
① D ② ア A イ $${\bm{\dfrac{9}{25}}}$$
この記事が気に入ったらサポートをしてみませんか?
