減法の意味（２）　ひき算の意味を網羅する

　ここでは便宜的に、小学校で習うたし算（非負数＋非負数）・ひき算（非負数ー非負数＝差が非負数）と、中学校で学習する負の数を含めた加法・減法を区別して表現する。

　算数教育学の本などを読むと「求残」「求差」「求補（求部分）」などのことばが並んでいる。ちょうど「和から」さんで、わかりやすい記事が出たので、これらの説明はそちらを。

　ところが小学１年で基数からスタートした加減が、中学に上がるまでに1～2の各場面で縦横無尽に使われることになる。3は「抽象化された数の加減の世界」である。

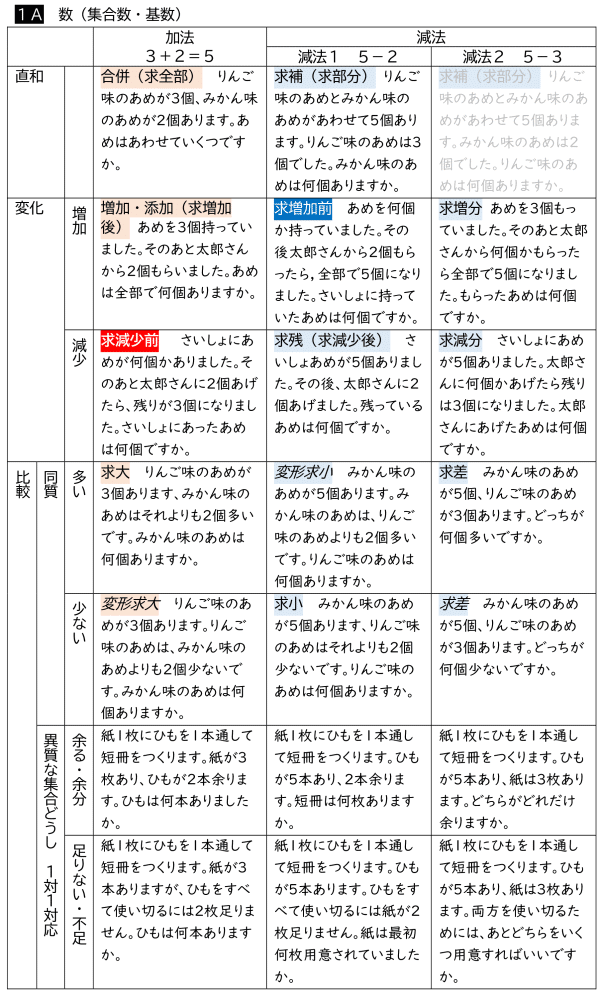
　ここで1～2の「素朴な」たし算・ひき算の意味の網羅を試みてみよう。このどれかが、たし算・ひき算の意味とされているのである。合併・増加、求残・求差・求補・求部分、求大・求小以外の言葉はは、とりあえずつけてみたものであり、標準的なもの（ネットを探して出てくるもの）ではない。

　3では、減法は代数的に「加法の逆演算」と定義される。Ｋｒ社以外の教科書は、その立場である。

　Ｇ社の引き算の答えの根拠は、図で直観的にと言うのでなく、文章でごちゃごちゃ説明しようとしたと言うところであろう。ひき算の意味としては、「求増分」と名づけたところにある。
　しかし求増分の減法がこれまでのひき算と大きく異なるのは、被減数（第１項）と減数（第２項）の決め方である。これまでの大小関係で決まっていた。6年間の間、嫌が応にもひき算の基本中の基本として叩き込まれてきたことであり、システム１として作動してきたはずである。ところが、ここで突然、大小関係にかかわらず、第1項は変化後、第２項は変化前という順序関係が持ち込まれる。時間経過である。これまでの6年間のトレーニングで減法では大小関係と作動していたシステム１に、システム２を割り込ませて、大小関係「ではなく」前後関係によって決定させる必要がある。引き算立式＝大小関係という強固なシステム1に抗わないといけない。当面はシステム2を割り込ませ、そのうちにシステム１として書き換えていく必要がある。
　この説明のために、いちいちシステム2をそもそも割り込ませる必要があるのか、というところでもある。

　それを解決しているのが、Ｋｒ社式の説明であるようにも思われる。すなわち、「○より△小さい数を求める計算が○－△」という定義は、小さいということばが日常的にもひき算を想起させるので、混乱が少ない、と考えられる。

　正負の数の減法を、日常の、というよりも素朴な、直観的なひき算に紐付けて定義するのはなかなか難しい。
　負の数の減法はそういう意味で、日常的な世界における意味づけを定義にするのであれば、とても困難にぶつかる。そして求答操作の上でも、なかなか厄介である。