茨城県｜公立高校入試確率問題2023

　下の図１のように［１］から［７］までの番号の書かれた階段がある。地面の位置に太郎さん、［７］の段の位置に花子さんがいる。太郎さん、花子さんがそれぞれさいころを１回ずつ振り、自分が出した目の数だけ、太郎さんは［１］、［２］、［３］、…と階段を上り、花子さんは［６］、［５］、［４］、…と階段を下りる。例えば、太郎さんが２の目を出し、花子さんが１の目を出したときは、下の図２のようになる。また、２段離れているとは、例えば、図３のような状態のこととする。

　このとき、次の（１）～（３）の間いに答えなさい。
　ただし、さいころは各面に１から６までの目が１つずつかかれており、どの目が出ることも同様に確からしいとする。

（１）　太郎さんと花子さんが同じ段にいる確率を求めなさい。

（２）　太郎さんと花子さんが２段離れている確率を求めなさい。

（３）　太郎さんと花子さんが３段以上離れている確率を求めなさい。

表の書き方の工夫

まず（１）を素朴に解いてみましょう。

　さいころ２回なので表、というのが定石です。

　で、ここからどうするか、ということですが、一つ一つたしかめていくことになるかな、と思います。
　　　太郎さんが★の目を出して［★］の段にいるとき
　　　　　　　　　↓
　　　花子さんが［★］の段にいるために必要な目
というのを、太郎さんの１～６の目ごとにリストアップする、というやり方ですすめてみましょう。
　（１回目のさいころの目の数，２回目のさいころの目の数）と表すことにして、説明しましょう。

〇太郎さんが１の目を出して［１］の段にいるとき
　花子さんが［１］の段に行くためには６の目を出せばよい。当てはまるのは（１，６）
〇太郎さんが２の目を出して［２］の段にいるとき
　花子さんが［２］の段に行くためには５の目を出せばよい。当てはまるのは（２，５）
〇太郎さんが３の目を出して［３］の段にいるとき
　花子さんが［３］の段に行くためには４の目を出せばよい。当てはまるのは（３，４）
〇太郎さんが４の目を出して［４］の段にいるとき
　花子さんが［４］の段に行くためには３の目を出せばよい。当てはまるのは（４，３）
〇太郎さんが５の目を出して［５］の段にいるとき
　花子さんが［５］の段に行くためには２の目を出せばよい。当てはまるのは（５，２）
〇太郎さんが６の目を出して［６］の段にいるとき
　花子さんが［６］の段に行くためには１の目を出せばよい。当てはまるのは（６，１）

　当てはまる組のところを表に印を入れると、次の通り。

　すべての場合の数は３６通りで、当てはまる場合の数は６通りですので、求める確率は$${\dfrac{6}{36}=\bm{\dfrac{1}{6}}}$$。

（２）の問題。表の工夫

　続けて（２）の問題です。まずは同じようにやってみましょう。

〇太郎さんが１の目を出して［１］の段にいるとき
　花子さんは［３］の段にいればよいので、４の目を出せばよい。当てはまるのは（１，４）
〇太郎さんが２の目を出して［２］の段にいるとき
　花子さんが［４］の段にいればよいので、３の目を出せばよい。当てはまるのは（２，３）
〇太郎さんが３の目を出して［３］の段にいるとき
　花子さんが［５］の段・・・だけではなく［１］の段でもオッケーです。このことに気をつけましょう。ですから、６か２の目を出せばよいということになります。当てはまるのは（３，６），（３，２）
〇太郎さんが４の目を出して［４］の段にいるとき
　花子さんが［６］の段か［２］の段にいればよいので、５か１の目を出せばよい。当てはまるのは（４，５），（４，１）
〇太郎さんが５の目を出して［５］の段にいるとき
　花子さんが［３］の段にいればよいので、４の目を出せばよい。当てはまるのは（５，４）
〇太郎さんが６の目を出して［６］の段にいるとき
　花子さんが［４］の段にいればよいので、３の目を出せばよい。当てはまるのは（６，３）

・・・とやってもいいのですが、表の書き方を工夫すると、もうちょっと表で考えることができそうです。それは何か、というと、表にあらかじめ
　　　　１回目★の目が出て、太郎が［★］の段にいる
　　　　２回目◆の目が出て、花子が［▲］の段にいる
というのを書き込んでおく、ということです。

　すると、書いてある段を見て、２段違う（差が２である）場合に印をつけていけばいいですので、上の作業も楽になります。（２）の場合が当てはまる場合に✓印を入れておきましょう。

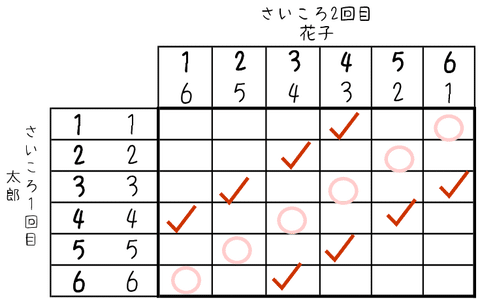
　当てはまるのは８通りですので、その確率は$${\dfrac{8}{36}=\bm{\dfrac{2}{9}}}$$と求めることができます。

そうすると、（３）も今までの表で解けますね。

　最後に（３）の問題。表を書いて考えるやり方を見ておきます。３段以上ですから、差が３以上ということで、当てはまる場合に△印を書き入れることにすると、

で、１２通りありますから、確率は$${\dfrac{12}{36}=\bm{\dfrac{1}{3}}}$$です。

答

（１）　$${\bm{\dfrac{1}{6}}}$$
（２）　$${\bm{\dfrac{2}{9}}}$$
（３）　$${\bm{\dfrac{1}{3}}}$$