
山梨県|公立高校入試統計問題2024
Bさんの中学校では,PC・タブレットなどのICT機器のキーボードを用いた文字入力の練習会を行っている。このとき,次の1,2に答えなさい。
1 Bさんは,所属する学年の生徒95人で行われた,ある日の練習会における1分間あたりの文字入力数を記録し、図1のようなヒストグラムに表した。また,長方形の上に示されている数は,それぞれの階級の度数を表している。このとき,次の(1),(2)に答えなさい。

(1) 中央値が含まれる階級を求めなさい。
(2) 1分間あたりの文字入力数が40文字以上の生徒の人数の割合は,全体の何%か求めなさい。
2 Bさんは,数か月後に行われた練習会で全校生徒285人を対象に1分間あたりの文字入力数を調べた。その際,1日あたりのICT機器を学習に用いた時間についても調べ,60分未満(①)の生徒と60分以上(②)の生徒に分け,それぞれについて相対度数を求め,右のような度数分布表に表した。

このとき,次の(1),(2)に答えなさい。
(1) 2つの分布の傾向を比べるために,相対度数を用いることについて,次のように理由を示した。[ X ]に当てはまるものを下のア~エから1つ選び,その記号を書きなさい。
理由 ①と②のそれぞれの[ X ]が異なるから。
ア 学習時間の合計 イ 最大値 ウ 範囲 エ 全体の度数
(2) 図2は度数分布表をもとに,横軸を文字入力数,縦軸を相対度数として度数分布多角形(度数折れ線)に表したものである。図2から「1日あたりのICT機器を学習に用いた時問が60分以上(②)の生徒は、60分未満(①)の生徒より,1分間あたりの文字入力数が多い傾向にある」と主張することができる。そのように主張することができる根拠を,2つの度数分布多角形の特徴を比較して説明しなさい。

1(1)中央値
1番ではデータの個数は95人分ですから,データを小さい値から順に並べたときに中央値は,
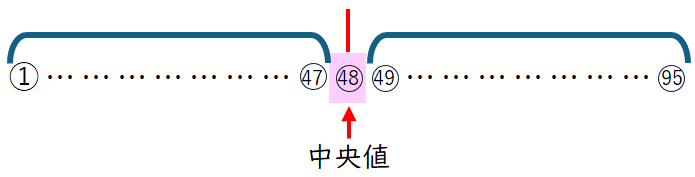
ちょうど【48】番目にあたるデータの値となります。ヒストグラムで累積度数を見ると,

【48】番目のデータは,ぎりぎり30文字以上40文字未満の階級にあります。
1(2)
ヒストグラムから40文字以上の度数

をすべてたして12+4+2+1=19でもいいですし,せっかくさっき40文字未満の累積度数を計算しているので95-76=19で求めてもいいでしょう。
あとは割合を百分率で求めますから
19÷95×100(=1900÷95)=20
という筆算,あるいは分数で
$${\dfrac{19}{95}×100=\dfrac{19*100}{95}=\dfrac{19×20}{19}=20}$$
という約分ができるかどうか,という問題,ということになります。
2(1)
相対度数とは,度数の合計に対するその階級の度数の割合です。全体の度数(総度数)が異なるデータを比較するときに,割合で比べる方が妥当ですね。
ですから,選択肢として選ぶのは,エの「全体の度数」です。
2(2)
2つの度数分布多角形を比べると
●分布の形は,ずらすとほぼ重なりそうな似た形をしています。
山が1つで,データの散らばり具合がほぼいっしょです。

●分布は,60分以上(②)の度数分布多角形が1分間あたりの文字入力数が多い右側の方に寄っています。
この2点を指摘して説明すればよいでしょう。
答
1 (1)30文字以上40文字未満 (2)20%
2 (1) エ
(2)(教育委員会による正答例)
2つの度数分布多角形は同じような形で,60分未満(①)の度数分布多角形よりも60分以上(②)の度数分布多角形の方が右側にあるから。
(別解) 2つの度数分布多角形は同じような形で,60分以上(②)の度数分布多角形よりも60分未満(①)の度数分布多角形の方が左側にあるから。
この記事が気に入ったらサポートをしてみませんか?
