【Pyxel】Pyxelで学ぶゲーム数学の基礎〜三角関数

2019年3月6日 11:00

今回も、レトロゲームエンジン「Pyxel」を使って、ゲームでよく使われる数学について学ぶ記事となります。

今回のテーマは「三角関数」です。三角関数というと何やら難しそうなイメージがありますが、理屈を抜きにしてゲーム開発に使えるところだけ覚えるとすれば、たったの3つなので、それほど難しいものではありません。
もちろん、原理や仕組みを理解すると、より高度なことができますが、最初は使いながら慣れていくのが良いのではないかと思います。

今回学ぶことは以下の3つです。

1. サインカーブで動きをつける方法
2. cos() / sin() で回転する方法
3. atan2() で狙い撃ちする角度を求める方法

2と3については、ジャンル別ゲームの作り方（2Dアクション・2Dシューティング）で説明したように、シューティングゲームを作る際に大活躍するテクニックとなります。

なお Pyxel のセットアップについては、以下のページにまとめていますので、まだインストールできていない場合は、こちらを参考にしてください。
【関連記事】：【Pyxel】セットアップ手順と基本の関数について

■1. サインカーブで動きをつける方法

サインカーブは、以下の図で説明ができます。

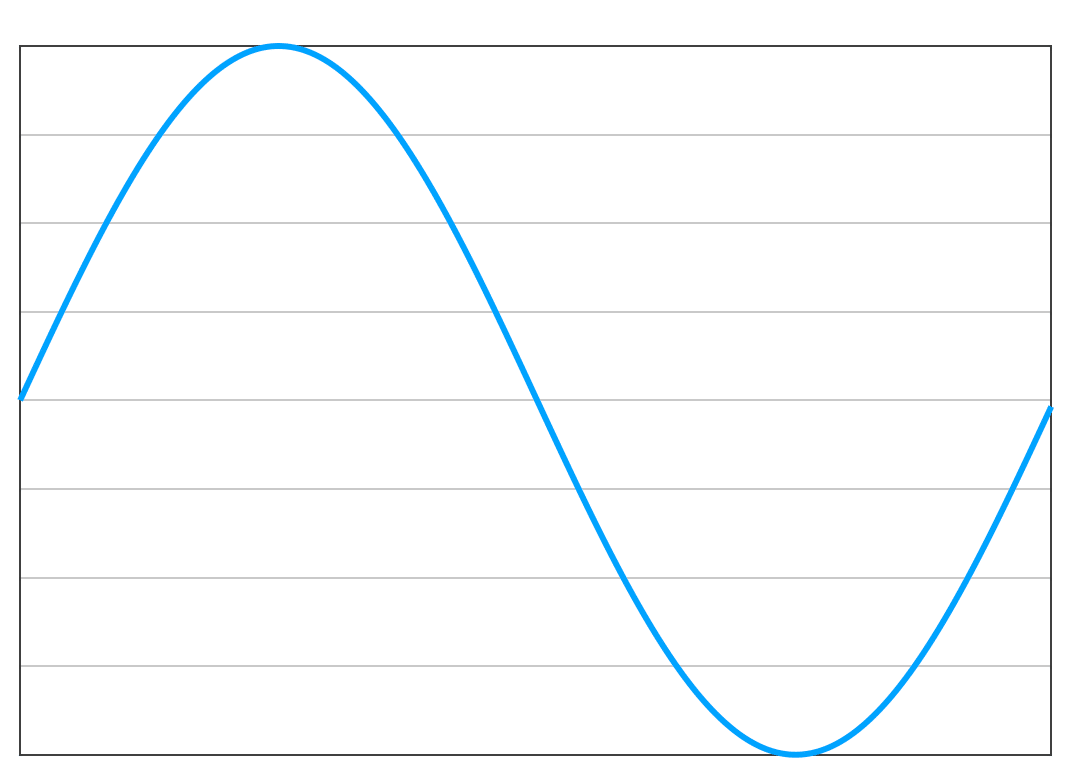
横軸を時間の経過とすると、縦軸は値の変化となります。サインカーブは波動や振動などの波を表現する方程式の一部として使われるのですが、これをキャラクターの動きに適用すると「ふわふわ」と浮かぶ動きになります。

ふわふわニャンコ様

ではこの動きを実装しましょう。まず、Pyxelを動かすための最小限のコードを用意します。

import pyxel

class App:
    def __init__(self):
        pyxel.init(160, 120, fps=60)
        pyxel.run(self.update, self.draw)

    def update(self):
        pass

    def draw(self):
        pass

App()

main.pyなどの名前で保存します。「python3 main.py」で実行すると何もない画面が表示されます。

続けて、サインカーブで動きをつけるコードを追記します。
修正箇所は以下の通りです。

▼修正箇所
・最初に import math で数学関連のモジュールをインポート
・class App の下に基準座標となる定数(BASE_X / BASE_Y)を追加
・__init__() で各種変数を初期化
・upate() で変数をキー入力で変更。座標情報(self.x / self.y)の更新
・draw() で円を描画。変数値をテキスト表示する

import pyxel
import math

class App:
    BASE_X = 80 # 基準座標(X)
    BASE_Y = 60 # 基準座標(Y)
    def __init__(self):
        pyxel.init(160, 120, fps=60)
        self.x = self.BASE_X
        self.y = self.BASE_Y
        self.timer = 0
        self.speed = 0.05 # 速度
        self.intensity = 40 # 揺れ幅
        pyxel.run(self.update, self.draw)

    def update(self):
        if pyxel.btn(pyxel.KEY_LEFT):
            self.speed -= 0.001 # 速度ダウン
        if pyxel.btn(pyxel.KEY_RIGHT):
            self.speed += 0.001 # 速度アップ
        if pyxel.btn(pyxel.KEY_UP):
            self.intensity += 0.4 # 振れ幅アップ
        if pyxel.btn(pyxel.KEY_DOWN):
            self.intensity -= 0.4 # 振れ幅ダウン

        self.timer += self.speed
        self.y = self.BASE_Y + self.intensity * math.sin(self.timer)

    def draw(self):
        pyxel.cls(0)
        # 円の描画
        pyxel.circ(self.x, self.y, 8, 9)

        # テキスト描画
        pyxel.text(0, 0, "SPEED:%f"%self.speed, 7)
        pyxel.text(0, 8, "INTENSITY:%f"%self.intensity, 7)
        

App()

実行して動作を確認します。

左右キーでゆらゆら動くスピード(SPEED)、上下キーで動きの幅の大きさ(INTENSITY)を変更できます。
update() に記述した計算式に注目してみましょう。

self.y = self.BASE_Y + self.intensity * math.sin(self.timer)

math.sin() に渡している self.timer の増加する速度が上がると、ゆらゆら動くスピードが上がります。

水色の線が基準となるサインカーブとすると、self.timer の増加率が上がるほど、緑色の線のように横につぶしたサインカーブとなります。上下移動の繰り返しが早まるということは速度が上昇し、より激しく動くようになる、ということです。

そして、math.sin() が返した値に対して、かけ算をすると振れ幅が大きくなります。

より大きく動かしたい場合は、かける値を大きくする。小さくしたい場合は、0.0 に近づけると振れ幅が小さくなります。

サインカーブのさらなる応用として、バウンドさせる動きができます。ソースコードの update() の部分を以下のように修正します。

self.y = self.BASE_Y + self.intensity * math.sin(self.timer%math.pi) * -1

math.sin() に渡している部分を math.pi の剰余とし、-1 をかけるようにしました。実行すると以下のようにバウンドした動きとなります。

なぜこのような動きになるのかというと、math.sin() に渡す値をサインカーブの周期の上半分のみとしたためです。(スクリーン座標系は下方向がプラスなので、-1をかけることで上向きに反転しています)

水色が元のサインカーブで、緑色が修正後のサインカーブです。（線が重なってしまうので、便宜上、緑色の振り幅を少し小さくしています）

サインカーブは 360度で一周して周期の最初に戻ります。それを180度で折り返すようにすると、0〜180度だけを繰り返し、バウンドする動きになる……、ということです。

問題は、「math.sin( self.timer % math.pi )」というように、math.pi で剰余を求めているところです。実はプログラム上で用意されている関数は、馴染みのある 0〜360度という度数法ではなく、0〜2π という弧度法による周期を使うことが多いためです。Python の math.sin() も引数に弧度法による値を受け取るため、このようなコードになっています。

なお、弧度法と度数法は互いに変換が可能で、ゲームライブラリ上にも変換関数が用意されていることが多いです。例えば Python では

# 弧度法から度数法へ変換
deg = math.degrees( rad )

# 度数法から弧度法に変換
rad = math.radians( deg )

というように相互に変換が可能です。データ入力上は、度数法の法が扱いやすいので、通常は、

度数法でデータを入力　→　プログラム側で弧度法に変換

という流れを取ることが多いです。
なお、度数法はディグリー(degree または deg)、弧度法はラジアン(radian または rad)と表記されることが多いので、まずはこの表記に慣れることが三角関数を自由自在に使うための第一歩となります。

あと、実際に使うとわかることですが、プログラム上は 0度〜90度〜180度〜270度〜360度というように、プラス方向で値を扱うのではなく、180度から360度の下半分はマイナスとして扱われます。

もちろん、270度や360度といった値も許容されていますが、atan2() などで得られる値について、右回りの下半分は負の値として扱われます。
これにより例えば、270度から180度へ回転させる際に必要な角度を求める場合は -90度を返してくれるので、そのまま足しこむだけで良いこととなります。

■2. cos() / sin() で回転する方法

cos() / sin() を使うと、ある点を基準に、角度と距離から円周上の点を求めることができます。

update() を以下のように修正します。

    def update(self):
        if pyxel.btn(pyxel.KEY_LEFT):
            self.speed -= 0.001 # 速度ダウン
        if pyxel.btn(pyxel.KEY_RIGHT):
            self.speed += 0.001 # 速度アップ
        if pyxel.btn(pyxel.KEY_UP):
            self.intensity += 0.4 # 振れ幅アップ
        if pyxel.btn(pyxel.KEY_DOWN):
            self.intensity -= 0.4 # 振れ幅ダウン

        self.timer += self.speed
        #self.y = self.BASE_Y + self.intensity * math.sin(self.timer%math.pi) * -1
        self.x = self.BASE_X + self.intensity * math.cos(self.timer)
        self.y = self.BASE_Y + self.intensity * -math.sin(self.timer)

サインカーブによる移動をしていたところを修正しています。

▼計算式
X座標＝半径 * math.cos(角度)
Y座標＝半径 * -math.sin(角度)

※ プログラム上は "intensity" を半径としています
※ math.cos() / math.sin() に渡す値は "ラジアン" ですが、上記の式ではわかりやすく角度としています
※ math.sin() にマイナスを掛け合わせているのは、スクリーン座標系の下方向がプラスなので、値を反転する必要があるためとなります

実行すると、円が画面を中心に回転します。

これが何の役に立つのかについては、ジャンル別ゲームの作り方（2Dアクション・2Dシューティング）に書いた通り、速度を「角度」「速さ(半径)」というゲームに使いやすいパラメータとして扱うことができるためです。

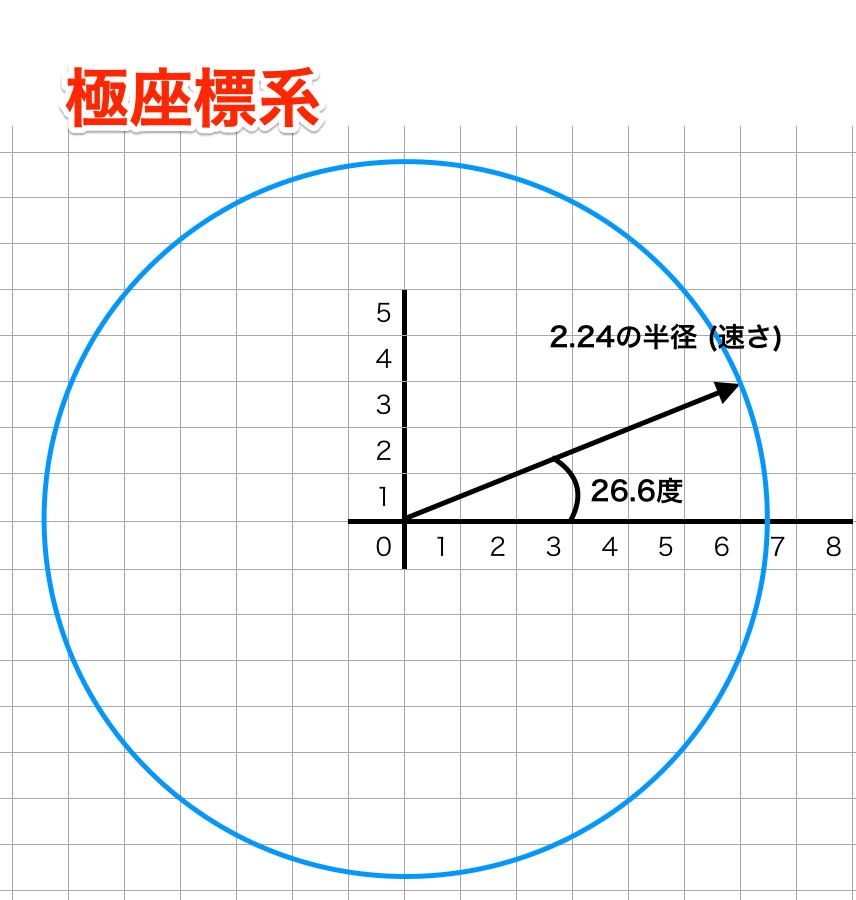
上記例であれば、速度を(x, y) = (6, 3) という扱いづらい値ではなく、26.6度と速さ「2.24」で管理できます。それによりゲームバランスの調整が楽になるわけです。

■3. atan2() で狙い撃ちする角度を求める方法

atan2() を使って、画面中心からマウスのある位置をめがけて動く処理を作ってみます。
まずは __init__() を修正します。

    def __init__(self):
        pyxel.init(160, 120, fps=60)
        self.x = self.BASE_X
        self.y = self.BASE_Y
        self.timer = 0
        self.speed = 0.05 # 速度
        self.intensity = 40 # 揺れ幅
        self.aim = 0 # 狙い撃ち角度
        pyxel.mouse(True) # マウスカーソルを表示する
        pyxel.run(self.update, self.draw)

変数 self.aim を追加し、マウスカーソルを表示する処理を追加しました。

続けて、update() の修正です。

    def update(self):
        if pyxel.btn(pyxel.KEY_LEFT):
            self.speed -= 0.001 # 速度ダウン
        if pyxel.btn(pyxel.KEY_RIGHT):
            self.speed += 0.001 # 速度アップ
        if pyxel.btn(pyxel.KEY_UP):
            self.intensity += 0.4 # 振れ幅アップ
        if pyxel.btn(pyxel.KEY_DOWN):
            self.intensity -= 0.4 # 振れ幅ダウン

        self.timer += self.speed
        if self.timer > 2:
            # 狙い撃ち角度を求める (単位はラジアン)
            dx = pyxel.mouse_x - self.BASE_X
            dy = pyxel.mouse_y - self.BASE_Y
            self.aim = math.atan2(-dy, dx)
            self.timer = 0

        #self.y = self.BASE_Y + self.intensity * math.sin(self.timer%math.pi) * -1
        self.x = self.BASE_X + self.intensity * self.timer * math.cos(self.aim)
        self.y = self.BASE_Y + self.intensity * self.timer * -math.sin(self.aim)

一定周期 (self.timer が 2を超える) で狙い撃ち角度を atan2() を使って求めます。 atan2() には、目標とする座標へのXY軸それぞれの距離を引き算で求めます。

▼計算式
dx ＝目標座標(X) - 起点となる座標(X)
dy ＝目標座標(Y) - 起点となる座標(Y)
# 目標への角度
rad = math.atan2(-dy, dx)

実行するとマウスカーソルめがけて丸が発射されます。

■最後に

最後の方は若干駆け足気味でしたが、三角関数を使ったゲーム数学の基本的な知識は以上です。
あとは、実際に使ってみて、どのような使い方をすると良い感じになるのかを模索していくと、自然と慣れていくと思います。

■参考書籍

今回の記事を書くにあたって参考にした本です。絶版のため中古本しかありませんが、安く買えます。

新品が良ければ、改訂版もあります。

こちらの本も具体的でわかりやすく、よりゲーム開発者目線の専門的な内容でオススメです。

■関連する記事

繰り返し書きましたが、三角関数はシューティングゲームを作るときに最大の威力を発揮します。むしろ必須と言えるほど……。
ゲームで使う三角関数の練習には、是非、シューティングゲームを一度作ってみることをオススメします。