書記が数学やるだけ#24 Star⭐︎puzzle （+手元にある数学系の本についていくつか）

#アドベントカレンダー 　の参加企画。

単純に見た目の面白さから選んだ。結果，中学の幾何から大学入試で差がつくネタまで網羅することになった。（普段の倍は書いている）

問題

正五角形を並べてできた図形についての問題。無限等比数列の和を求めることで数Ⅲっぽい感じにした。cos72°は色々な解き方があるが，本問では見ただけでわかるようにした。

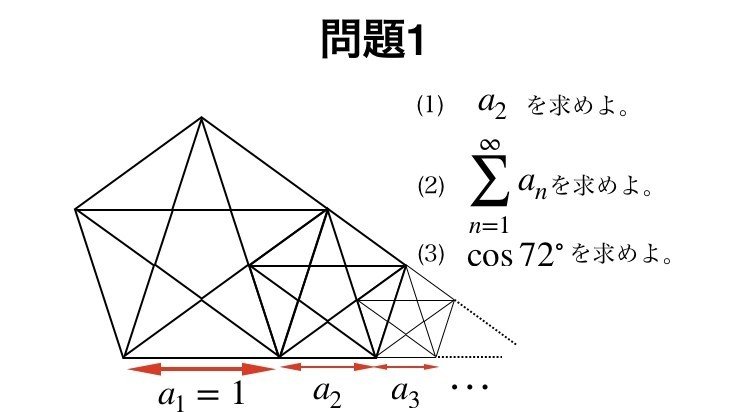
考え方の基本は中学の幾何でやるようなもので，私立高校受験レベルまで落とし込んだものがこちら（といっても多分実際の私立高校受験はこんな簡単ではないと思う）。

もう一つ，こちらは実際の大学入試の問題。

そのほか正五角形にまつわる問題は2018広島県大や2019東京理科大（薬），2020横浜市大，2021順天堂大などで出題されている，ベクトルと絡めてくるケースもある（実際はほぼ中学レベルだったりする）。

関連する小問についても，ここでまとめて解説する。

問題1解法

まず，正五角形の性質について。相似を活用する。

正五角形には黄金比が含まれている。

導出は一回はやっておく。

では問題へ。

a1とa2の関係が図を見て分かるかどうか。

a2とa3，a3とa4と以後同じように見ていくと，それぞれが「対角線：1辺」となるのがわかる。ということはanは等比数列である。公比の絶対値が1より小さいなら無限和は収束することを利用して，値を求める。

cos72°についてはいろいろな解き方がある。今回は直角三角形が見えるので，そこから直接求めた。この他，36°，72°，108°などの三角関数は解き方を覚えておくと有利。

問題1高校受験ver.解法

高校入試ver.では，相似を複数回用いて解くほかに，二等辺三角形を見つけて解く，などなど様々な解答があると思う。

ここで，黄金比の性質についてまとめておく。

問題2解法

「大正五角形の1辺：小正五角形の1辺」は，正五角形の性質を応用することで求められる。

公比については，辺の長さの比が分かってるのだから，面積比を出すのは容易だろう。この問題の厄介なところは「正五角形の面積」である（誘導なしだと計算量的に難問に化ける）。3つの三角形に分けるだけでも解けなくはないが，少しでも楽をするために等積変形を利用した。

この二重根号は，外れない。そういうこともあると割り切る姿勢が重要。原題はマークシート式で，二重根号が含まれることは示されており，見た瞬間に絶望するかもしれないが，解き進めることができた人にとっては大きな安心材料なのだろう。

小問解法

10乗を素手で解くのはきつい。まず2乗してみると，良い性質に気づく。

いわゆる次数下げができるので，それを使って順次解いてみる。

ここで係数を見ると，フィボナッチ数列に対応しているのが見えてくる（察しのいい方は，φ^2=φ+1がフィボナッチ数列の一般項に対応しているのが見えたのでは）。これより10乗の係数が求められる。

片方だと√5が混じり無理数だというのはなんとなく想像がつくが，両者を合わせると整数になる。これはどういうことなのか。

数学的帰納法で証明するのだが，k+1からkの式を出そうとすると，どうしてもk-1の式が出てきてしまう。よって2つ前までが正しいと仮定する必要がある，俗におととい帰納法と呼ばれているものである。

なお，関連する内容の記事を既に上げているのでこちらも参考に。

手元にある数学系の本についていくつか

これらは記事の元ネタになったりする。

・これなら分かる最適化数学―基礎原理から計算手法まで―

これなら分かる最適化数学―基礎原理から計算手法まで

わかりやすさと実例の多さの点でおすすめできる。ある程度の数学（微分積分と線形代数）は前提として必要だが，前半で必要な道具も示されている。特に最小二乗法を具体例で理解したい時に重宝する。

内容：

1次形式と2次形式/関数の極値/最適化の手法（ニュートン法など）/最小二乗法/最尤推定/線形計画法/非線形計画法/動的計画法

・数学から創るジェネラティブアート - Processingで学ぶかたちのデザイン

数学から創るジェネラティブアート ―Processingで学ぶかたちのデザイン

見てるだけで面白いし（ここ重要），背景となる数学も興味深いものばかり。実際にプログラミングしながら作図できるのも良い。

内容：

ユークリッドの互除法/連分数/フィボナッチ数列/対数らせん/フェルマーらせん/合同式/セルオートマトン/群論の導入（対称性や周期性など）

・ストロガッツ 非線形ダイナミクスとカオスー数学的基礎から物理・生物・化学・工学への応用まで

ストロガッツ 非線形ダイナミクスとカオス

前提知識は相当必要（特に微分方程式）だが，力学系の本ではわかりやすい方という印象，とにかく説明が丁寧。生物の挙動を数学的に解析するには必須だろう。

内容：

微分方程式/解の安定性，分岐，振動子/相平面/リミットサイクル/ローレンツ方程式/1次元写像/フラクタル

・弱点克服　大学生の確率・統計

弱点克服 大学生の確率・統計

数理統計のための演習書として使った。実例が多いので使いやすかった。後半では金融数学やアクチュアリーについても触れられている。

内容

確率分布の概念と計算（期待値，分散，モーメント母関数など）/離散確率分布（二項分布，ポアソン分布など）/連続確率分布（正規分布，指数分布，t分布など）/多次元確率分布/推測統計学/確率過程/金融数学やアクチュアリーの導入

まとめ

量が多かったので，ここでまとめ。

・正五角形には黄金比が含まれている

・黄金比とフィボナッチ数列との関係は不可分である

本記事のもくじはこちら：