【高校数学】2次不等式②

1．はじめに

2次不等式について、「解はすべての実数」だったり、「解はなし」だったりする場合ってどういうこと？？？という方、必見です！
よくわからないけど、パターンを覚えるか、、、そんな必要はありません。図で考えれば、すべて解決します！

今日は、主にこの4問を解説します。定数項のみが異なりますが、解は全く異なります。

2．(1)(2)の解について

まずは、(1)について

図で考えなくてもわかる方も、ぜひ図での理解もしましょう。図で理解することが、「解はすべての実数解」「解はなし」の場合の理解につながります。

(1)を図で考えるのを詳しく知りたい方は、こちらを先に読んでください。

では、(2)はどうでしょうか？

こちらは、(1)と違い、因数分解ができません。その場合は、解の公式を用いれば、解くことができますね。

方程式の解の出し方が異なるだけで、不等式の解は(1)と同様に考えることができます。

3．(3)の解について

では、いよいよ(3)です。

こちらも、(2)と同様に、左辺が因数分解できないので、解の公式を用います。

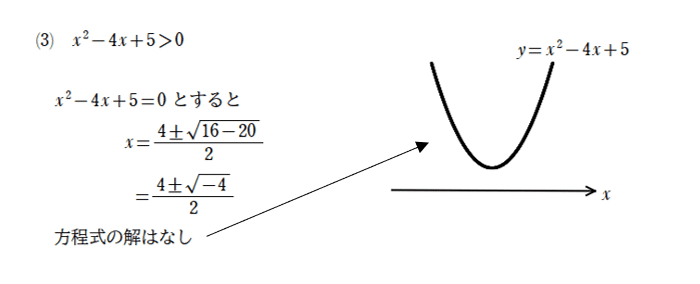
すると、ルートの中がマイナスになってしまい、実数解が存在しないのですね。ということは、グラフは、x軸とぶつかりません。(1)、(2)では、解が2個だったため、グラフがx軸と2か所でぶつかっていました。
では、解を見てみましょう。

不等号が＞のため、0より大きいので、グラフはx軸より上が対応します。グラフはx軸よりも上にあるため、すべてのxが対応し、すべてのxが解です。

それでは、不等号が異なった場合も見てみましょう。

不等号が＜のため、0より小さいので、グラフはx軸より下が対応します。グラフはx軸よりも下にはないため、すべてのxが対応せず、解はなしです。

不等号が≧のため、0以上なので、グラフはx軸より上とx軸が対応します。グラフはx軸よりも上にあるため、すべてのxが対応し、すべてのxが解です。

不等号が≦のため、0以下なので、グラフはx軸より下とx軸が対応します。グラフはx軸よりも下にはなく、x軸にもないため、すべてのxが対応せず、解はなしです。

4．(4)の解について

では、最後に、(4)について考えましょう。

こちらは、左辺が因数分解できますね。

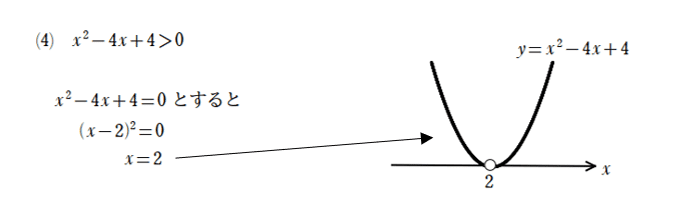
しかし、解が2個ではなく1個のため、グラフはx軸と1か所でぶつかります。では、解を見てみましょう。

不等号が＞のため、0より大きいので、グラフはx軸より上が対応します。グラフはx=2以外の部分は、x軸よりも上にあるため、2以外のすべてのxが対応し、2以外のすべてのxが解です。

それでは、不等号が異なる場合も見てみましょう。

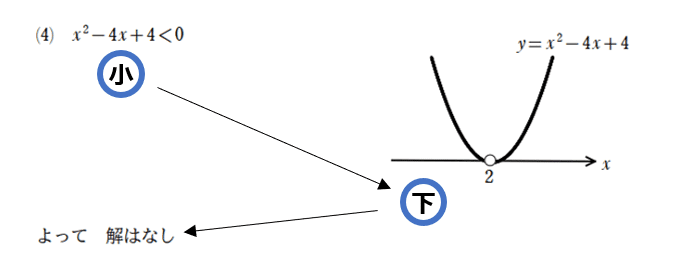
不等号が＜のため、0より小さいので、グラフはx軸より下が対応します。グラフはx軸よりも下にはないため、すべてのxが対応せずし、解はなしです。

不等号が≧のため、0以上なので、グラフはx軸より上とx軸が対応します。グラフはx軸よりも上とx軸にあるため、すべてのxが対応し、すべてのxが解です。

不等号が≦のため、0以下なので、グラフはx軸より下とx軸が対応します。グラフはx軸よりも下にはないが、x=2の部分はx軸にあるため、x=2のみ対応し、x=2のみが解です。

5．おわりに

なぜ、「解はすべての実数」だったり、「解はなし」だったりする場合があるか、理解できたでしょうか？
図を用いれば、パターンを覚える必要はありません。数学は、考えるからおもしろいのであり、覚えようという感覚ではつまらなくなってしまうと思います。1回1回考えることを大切にしていきましょう。