【高校数学】2次不等式①

1．はじめに

2次不等式について、

どのように答えますか？

ここまではできるけど、、、答え方は

どうだっけ？という方、必見です！

ちなみに答えはこちらです。

(1)～(4)　2次不等式を不等号別に、(5)～(6)　連立不等式を解説します。

2．2次不等式

不等式は図を使うと簡単に解けます。図というのはグラフです。不等式の前に、方程式とグラフの関係について確認しましょう。

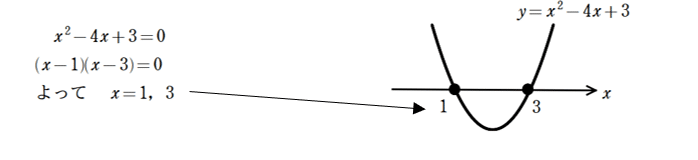
方程式の解は、2次関数のグラフとx軸(y=0)との交点のx座標に対応します。これを用いて、不等式を解いていきましょう。

不等号＞の意味ですが、「大きい」＞「小さい」です。

(1)では、不等号が＞のため、0より大きいので、グラフはx軸より上が対応します。それに対応するxが解です。1より左側と3より右側ですね。そして、解の書き方ですが、x軸に着目すると簡単です。ポイントは、x軸は右にいくほど大きいです。そのため、小さい順に表すと、x→1→3→xです。そして、右が大きい不等号＜を用いれば、x＜1、3＜xです。

(2)では、不等号が＜のため、0より小さいので、グラフはx軸より下が対応します。解は、1と3に挟まれますね。小さい順に表すと、1→x→3です。そして、右が大きい不等号＜を用いれば、1＜x＜3です。

(3)(4)では、(1)(2)に＝がついているだけです。図では、=では含まれるということで、黒丸を用います。(1)(2)のように、=がない場合は、含まれなということで、白丸を用います。解を答えるときも=を忘れないでください。

3．連立不等式

連立不等式について、解説します。連立不等式は、2つ以上の式を満たすものが解です。そのため、1つずつ解き、それらの共通解を求めればよいです。

ここでも、共通解の書き方は、x軸に着目すればよいです。小さい順に、2→x→3なので、2＜x＜3が解です。

(6)のように、共通解が2つの式で表されることもあります。しかし、図を用いればどんな場合でも怖いものなしです。

4．おわりに

図を用いれば、パターンを覚える必要はありません。数学は、考えるからおもしろいのであり、覚えようという感覚ではつまらなくなってしまうと思います。1回1回考えることを大切にしていきましょう。

次回は、解がすべての実数だったり、なしだったりと、より多くのパターンを扱います。ですが、パターンを覚える必要はありません。図で考えればいいのです。