
【線形代数】1 ベクトルと外積
こんにちは、これが377本目の記事となったすうじょうです。今日は、大学数学の解説記事です。今回の内容は、線形代数よりベクトルを解説します。本記事は一部高校数学と同じ内容を含みますが、大学数学の記事として書いています。
線形代数の重要性
かつて、行列に関しては基礎部分が高校数学Cに含まれていた。しかし、現在は高校数学から消え、大学で習うことになっている。現在の高校数学において、これに近い単元はベクトルである。線形代数の重要な部分としては、連立方程式の解き方やその性質に注目することである。また、他の数学分野と切り離せない関係にあり、微積分などを学習するうえでも必要なことから、大学数学の基礎といえる。
行列は様々な分野で用いられている。私の専門分野である情報系でいえば、機械学習の理論やデータサイエンス、画像処理などで用いられている。理系に限らず、文系でも例えば経済学においては、ある産業の波及効果の総和を求めるのにレオンチェフ逆行列が用いられていたりする。
ちなみに、線形とは1次関数の直線($${y=ax+b}$$)のことと思えばよい。線形と、この対義語の非線形は大学でよく使われる言葉である。
このシリーズでは、すべての定理・公式・性質について証明は行わないが、線形代数の定理の証明は理解してほしいので、各自で教科書等を読んでほしい。また、具体的な話もあるが、抽象的な部分もあるので大学数学に慣れるためにも理解してほしい。ただ、分かりにくい部分は適時説明を入れることを心掛けている。前提となる知識としては、高校数学の基本的な部分が分かっていればよい。
このシリーズでは、大学の「線形代数」の講義でよく扱われる部分について解説する。なお、かつて数学Cに含まれていた内容については、シリーズの適切な位置に組み込む。
ベクトル
高校におけるベクトル
高校数学の数学B(新課程では数学C)において、登場したベクトルについて簡単に復習したうえで、線形代数の導入としてベクトルについて説明する。
高校においては、始点と終点が与えられて、座標空間や図形上で$${\overrightarrow{OA}}$$などと表す。または、基準となる原点$${O}$$があるうえで、ある点の位置を示すために$${\overrightarrow{a}}$$などと表した。
また、ベクトルが$${x,y}$$方向にどれだけ移動するか$${\overrightarrow{a}=(1,2)}$$のように成分で表せる。
そして、ベクトルは有向線分で、長さが大きさ、矢印の方向が向きという情報を含んでいる。以下の図のようなイメージである。
以上が高校数学におけるベクトルの簡単な復習である。
大学におけるベクトル
ここからは、大学においてよく書かれる方法でベクトルについて説明する。
$${n}$$個の数値の組を$${n}$$次元ベクトルという。ベクトルは、例えば
$$
\bm{a}=\begin{pmatrix}
1 \\
2
\end{pmatrix}
,
\bm{b}=\begin{pmatrix}
1 \\
2 \\
3 \\
4
\end{pmatrix}
$$
のように書く。このように、高校と異なり大学では多くの場合、ベクトルは上に矢印がなく、アルファベット小文字を太字(ボールド体)で書くことが多い。零(ゼロ)ベクトルについては、$${\bm{0}}$$と書く。
また、成分の書き方も横ではなく縦に並べて書き、これを列ベクトルという。成分を横に並べて書くベクトルは、行ベクトルといい、$${\bm{a}=(1 2)}$$のように書く。ただ横に並べて書く場合は、$${\bm{a}^T=(1 2)}$$や$${\bm{a}=(1 2)^T}$$、$${\bm{a}={}^t(1 2)}$$などと、列ベクトルの転置にすることが多い。ただ、横に並べて成分を書く場合、分かりづらいので、各成分の間に「,」が入ることがある。
※行列の転置については次回説明する。
※ベクトルの括弧について
ベクトルの表記で
$$
\bm{a}=\begin{bmatrix}
1 \\
2
\end{bmatrix}
$$
と書かれていることもある。
※ベクトルの太字について
教科書等では基本的に太字で書かれるが、太字かどうか分かりにくい場合や誤植で太字になっていない場合があるので注意する。
また、板書やノートに書くときは、太字が難しいので黒板太字といわれるアルファベットに線を一つ加えたもので書く。ただ、この書き方については個人差がある。以下のサイトにその一例がある。
※ベクトルの図示について
4次元以上のベクトルは、4次元平面を書くことができないことから、図示することが困難である。
※ベクトルの向きと方向について
ベクトルは、大きさと向きの情報を持つとしたが、大きさと向き、方向を持つと説明される場合もある。この場合、向きは矢印が向いているほうを指し、方向はベクトルの矢印を含む直線(矢印が向いているほうとその逆向きのほう)を指す。
ベクトルの一意性
ベクトルは基本ベクトルを用いて一意に表せる。以下は3次元の場合の説明である。
基本ベクトルとは、座標空間において$${x}$$軸、$${y}$$軸、$${z}$$軸上の正の向きの単位ベクトル(大きさが1のベクトル)で、それぞれ
$$
\bm{e}_x=\begin{pmatrix}
1 \\
0 \\
0
\end{pmatrix}
,
\bm{e}_y=\begin{pmatrix}
0 \\
1 \\
0
\end{pmatrix}
,
\bm{e}_z=\begin{pmatrix}
0 \\
0 \\
1
\end{pmatrix}
$$
となる。これを用いて、3次元の任意のベクトル$${\bm{a}}$$は$${\bm{a}=c_1\bm{e}_x+c_2\bm{e}_y+c_3\bm{e}_z(c_1,c_2,c_3 \in \Bbb{R})}$$と表し、これは一意性を満たす。($${\Bbb{R}}$$は実数全体の集合を意味する)つまり、これを満たす係数$${c_1,c_2,c_3}$$はただ一つである。以下でその証明をする。
$${\bm{a}=c_1\bm{e}_x+c_2\bm{e}_y+c_3\bm{e}_z(c_1,c_2,c_3 \in \Bbb{R})}$$は一意性を満たす
[証明]
$${\bm{a}}$$を2通りで表すことができると仮定する.
つまり,
$${\bm{a}=a_1\bm{e}_x+a_2\bm{e}_y+a_3\bm{e}_z, \bm{a}=b_1\bm{e}_x+b_2\bm{e}_y+b_3\bm{e}_z(a_1,a_2,a_3,b_1,b_2,b_3 \in \Bbb{R})}$$
このとき,
$${a_1\bm{e}_x+a_2\bm{e}_y+a_3\bm{e}_z=b_1\bm{e}_x+b_2\bm{e}_y+b_3\bm{e}_z}$$が成り立つ.
$${(a_1-b_1)\bm{e}_x+(a_2-b_2)\bm{e}_y+(a_3-b_3)\bm{e}_z=\bm{0}}$$
$${(a_1-b_1)\bm{e}_x+(a_2-b_2)\bm{e}_y+(a_3-b_3)\bm{e}_z=0\bm{e}_x+0\bm{e}_y+0\bm{e}_z}$$
係数を比較すると,
$${a_1-b_1=0, a_2-b_2=0, a_3-b_3=0}$$
$${a_1=b_1,a_2=b_2,a_3=b_3}$$
よって, 一意性を満たす $${\Box}$$
2次元の場合は任意のベクトルを$${\bm{a}=c_1\bm{e}_x+c_2\bm{e}_y(c_1,c_2 \in \Bbb{R})}$$と表せ、以下の図がそのイメージである。
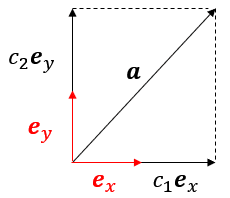
基本ベクトル表示の係数$${c_1,c_2,c_3}$$はそれぞれベクトルの$${x}$$成分、$${y}$$成分、$${z}$$成分の値に対応している。
※基本ベクトルについて
基本ベクトルはここでは、$${\bm{e}_x,\bm{e}_y,\bm{e}_z}$$と書いたが、物理などではよく$${\bm{i},\bm{j},\bm{k}}$$と書かれる。
内積・外積とベクトルの大きさ
内積(スカラー積)
以下は3次元の場合の説明である。
ベクトル$${\bm{a}=(a_x \space a_y \space a_z)^T}$$とベクトル$${\bm{b}=(b_x \space b_y \space b_z)^T}$$をかけて、スカラー(実数)となる積をベクトルの内積、スカラー積またはドット積といい、$${(\bm{a},\bm{b})}$$、$${\langle\bm{a},\bm{b}\rangle}$$または$${\bm{a} \cdot \bm{b}}$$と表す。この定義は以下のように書くことができる。
$${(\bm{a},\bm{b})=a_xb_x+a_yb_y+a_zb_z}$$
また、内積は以下のように行列の積として表現することもできる。
$$
\bm{a}^T\bm{b}=\begin{pmatrix}
a_x & a_y & a_z
\end{pmatrix}
\begin{pmatrix}
b_x \\
b_y \\
b_z
\end{pmatrix}
=a_xb_x+a_yb_y+a_zb_z
$$
※行列の積については次回説明する。また、$${\bm{b}^T\bm{a}}$$と表現してもよい。
ベクトルの大きさ(ノルム)
以下は3次元の場合の説明である。
ベクトル$${\bm{a}= (a_x \space a_y \space a_z)^T}$$の大きさ(長さ、ノルム)を$${\lVert\bm{a}\rVert}$$と表す。この定義は以下のように書くことができる。
$${\|\bm{a}\| = \sqrt{(\bm{a},\bm{a})} = \sqrt{a_x^2+a_y^2+a_z^2}}$$
※ノルムについて
$${\|\bm{a}\|}$$のことを$${L_2}$$ノルムまたはユークリッドノルムということがある。$${L_2}$$ノルムであることを強調するときは、$${\|\bm{a}\|_2}$$などと書く。
一般に$${1 \leq p < \infty}$$のとき、$${n}$$次元ベクトル$${\bm{a}= (a_1 \space a_2 \space \cdots \space a_n)^T}$$の$${L_p}$$ノルムは
$${\|\bm{a}\|_p = \sqrt[p]{|a_1|^p+|a_2|^p+…+|a_n|^p}}$$
となる。
2つのベクトル$${\bm{a}, \bm{b}}$$のなす角を$${\theta(0\leq\theta\leq\pi)}$$とするとき、内積と大きさ、なす角のあいだには以下の関係が成り立つ。
$${(\bm{a},\bm{b}) = \|\bm{a}\|\|\bm{b}\|\cos\theta}$$
これをなす角について、式を変形すると以下のようになる。
$${\cos\theta = \dfrac{\|\bm{a}\|\|\bm{b}\|}{(\bm{a},\bm{b})}}$$
特に$${\theta = \dfrac{\pi}{2}}$$のとき、$${\bm{a}}$$と$${\bm{b}}$$は直交($${\bm{a} \perp \bm{b}}$$)する。このことは、$${(\bm{a},\bm{b})=0}$$と同値である。
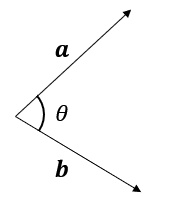
内積とベクトルの大きさについて、詳しくはこのシリーズでもう一度取り扱う。
外積(ベクトル積)
3次元ベクトル$${\bm{a}=(a_x \space a_y \space a_z)^T}$$と3次元ベクトル$${\bm{b}=(b_x \space b_y \space b_z)^T}$$をかけて、ベクトルとなる積をベクトルの外積、ベクトル積、またはクロス積といい、$${\bm{a} \times \bm{b}}$$と表す。この定義は以下のようになる。
向き:$${\bm{a}}$$と$${\bm{b}}$$の始点をそろえたときに2つのベクトルが作る平行四辺形に垂直な方向で、$${\bm{a}}$$を$${180\degree}$$以内の回転で$${\bm{b}}$$に重ねるために進む方向に、右ねじを回したときに右ねじが進む方向
大きさ:$${\bm{a}}$$と$${\bm{b}}$$の始点をそろえたときに2つのベクトルが作る平行四辺形の面積
向きについて、ややこしいので以下の図を用いて説明する。右ねじの方向については、物理の電磁気における「右ねじの法則」と同じように右手を使って説明する。$${\bm{a}}$$が$${\bm{b}}$$に重なるような向きに、右手の親指以外の4本の指をまわす。このとき、親指の向きが外積$${\bm{a} \times \bm{b}}$$の向きである。
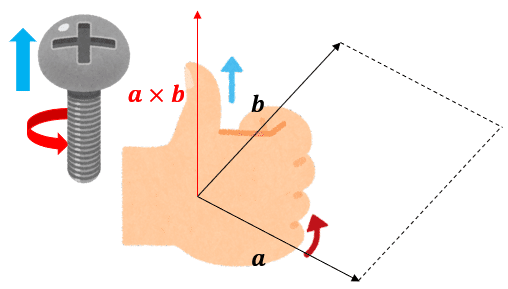
$${\bm{a}=(a_x \space a_y \space a_z)^T}$$と$${\bm{b}=(b_x \space b_y \space b_z)^T}$$に対して、外積$${\bm{a}\times\bm{b}}$$の成分表示は以下のようになる。
$$
\bm{a} \times \bm{b}=\begin{pmatrix}
a_yb_z-a_zb_y \\
a_zb_x-a_xb_z \\
a_xb_y-a_yb_x
\end{pmatrix}
$$
外積の成分表示について、基本ベクトルを用いた行列式で、以下のように形式的に表現することもできる。
$$
\begin{aligned}
\bm{a} \times \bm{b}&=\begin{vmatrix}
\bm{e}_x & \bm{e}_y & \bm{e}_z\\
a_x & a_y & a_z\\
b_x & b_y & b_z
\end{vmatrix} \\ \\
&=(a_yb_z-a_zb_y)\bm{e}_x+(a_zb_x-a_xb_z)\bm{e}_y+(a_xb_y-a_yb_x)\bm{e}_z
\end{aligned}
$$
※行列式については、後でこのシリーズで説明する。
※外積の成分表示の覚え方
覚え方については、ネットで様々なものが見つかるが、ここではその一例を紹介する。以下のように、それぞれのベクトルの最後に$${x}$$成分を付け足したものを並べる。
$$
\begin{pmatrix}
a_x \\
a_y \\
a_z \\
a_x
\end{pmatrix}
\begin{pmatrix}
b_x \\
b_y \\
b_z \\
b_x
\end{pmatrix}
$$
外積の$${x}$$成分を求めたいときは、1行目の$${a_x}$$と$${b_x}$$を隠して、求めたい成分以外の$${y,z}$$成分について、隠した部分を通過せずに(\でかけたもの)-(/でかけたもの)とクロスで計算する。これを同様に$${y}$$成分(2行目を隠す)と$${z}$$成分(3行目を隠す)についても行う。
以下に外積の性質をまとめて紹介する。証明については省略する。
・ベクトルを入れ替える
$${\bm{a} \times \bm{b}=-\bm{b}\times\bm{a}}$$
・分配法則(演算は掛け算のように展開することができる)
$${\bm{a} \times (\bm{b}+\bm{c})=\bm{a}\times\bm{b}+\bm{a}\times\bm{c}}$$
$${(\bm{a} + \bm{b}) \times \bm{c}=\bm{a}\times\bm{c}+\bm{b}\times\bm{c}}$$
・スカラー倍
$${c(\bm{a}\times\bm{b})=(c\bm{a})\times\bm{b}=\bm{a}\times(c\bm{b})}$$
・同じベクトルの外積
$${\bm{a}\times\bm{a}=\bm{0}}$$
・零ベクトルとの外積
$${\bm{a}\times\bm{0}=\bm{0}\times\bm{a}=\bm{0}}$$
・基本ベクトルの外積
$${\bm{e}_x \times \bm{e}_y = \bm{e}_z, \bm{e}_y \times \bm{e}_z = \bm{e}_x, \bm{e}_z \times \bm{e}_x = \bm{e}_y}$$
・外積の大きさ(平行四辺形の面積)
$${\|\bm{a}\times\bm{b}\|=\sqrt{\|\bm{a}\|^2\|\bm{b}\|^2-(\bm{a},\bm{b})}=\|\bm{a}\|\|\bm{b}\|\sin\theta}$$
・外積ともとのベクトルの関係
$${\bm{a}\times\bm{b} \perp \bm{a}\Leftrightarrow(\bm{a}\times\bm{b})\cdot\bm{a}=0, \bm{a}\times\bm{b} \perp \bm{b}\Leftrightarrow(\bm{a}\times\bm{b})\cdot\bm{b}=0}$$
・ベクトルの平行条件
$${\bm{a}\times\bm{b}=\bm{0} \Leftrightarrow \bm{a} /\!/ \space\bm{b}}$$
・平行六面体
$${\bm{a},\bm{b},\bm{c}}$$の始点をそろえたときに3つのベクトルが作る平行六面体の体積は$${|(\bm{a}\times\bm{b},\bm{c})|}$$
※外積は交換法則(演算の順序を交換できる)、結合法則(演算の優先順位を変更しても結果は変わらない)が成り立たない。基本ベクトルの外積について、他のものについては上の性質を使えばすぐに導出できるので書いていない。
※外積の大きさは、三角形の面積$${\dfrac{1}{2}\|\bm{a}\|\|\bm{b}\|\sin\theta}$$の2倍となっており、平行四辺形の面積と一致する。
演習問題1
問題1 $${\bm{a}=(3 5 1)^T,\bm{b}=(1 3 2)^T}$$とするとき、次の各問に答えよ。
(1)$${(\bm{a},\bm{b})}$$を求めよ。
(2)$${\|\bm{a}\|,\|\bm{b}\|}$$をそれぞれ求めよ。
(3)$${\bm{a}, \bm{b}}$$のなす角を$${\theta(0\leq\theta\leq\pi)}$$とするとき、$${\cos\theta}$$を求めよ。
(4)$${\bm{a}\times\bm{b},\bm{b}\times\bm{a}}$$をそれぞれ求めよ。
[解答]
(1)
$${(\bm{a},\bm{b})=3\cdot1+5\cdot3+1\cdot2=20}$$
(2)
$${\|\bm{a}\|=\sqrt{3^2+5^2+1^2}=\sqrt{35}}$$
$${\|\bm{b}\|=\sqrt{1^2+3^2+2^2}=\sqrt{14}}$$
(3)
$${\cos\theta = \dfrac{\|\bm{a}\|\|\bm{b}\|}{(\bm{a},\bm{b})}=\dfrac{\sqrt{35}\cdot\sqrt{14}}{20}=\dfrac{7\sqrt{10}}{20}}$$
(4)
$$
\bm{a}\times\bm{b}=\begin{pmatrix}
5\cdot2-1\cdot3 \\
1\cdot1-3\cdot2 \\
3\cdot3-5\cdot1
\end{pmatrix}
=\begin{pmatrix}
7 \\
-5\\
4
\end{pmatrix}
\\
\bm{b}\times\bm{a}=\begin{pmatrix}
3\cdot1-5\cdot2 \\
2\cdot3-1\cdot1 \\
1\cdot5-3\cdot3
\end{pmatrix}
=\begin{pmatrix}
-7 \\
5\\
-4
\end{pmatrix}
$$
※(4)について、$${\bm{a} \times \bm{b}=-\bm{b}\times\bm{a}}$$を利用してもよい。
問題2 $${\bm{a}=(a_x a_y a_z)^T,\bm{b}=(b_x b_y b_z)^T}$$とするとき、
$$
\bm{a} \times \bm{b}=\begin{pmatrix}
a_yb_z-a_zb_y \\
a_zb_x-a_xb_z \\
a_xb_y-a_yb_x
\end{pmatrix}
$$
となることを証明せよ。ただし、外積の性質を用いてよい。
[方針]
外積の性質を使えるようにするために、基本ベクトル表示をする
外積は分配法則は成り立つが、交換法則は成り立たないので注意する
[証明]
$$
\begin{aligned}
\bm{a}\times\bm{b}&=(a_x\bm{e}_x+a_y\bm{e}_y+a_z\bm{e}_z)\times(b_x\bm{e}_x+b_y\bm{e}_y+b_z\bm{e}_z)\\
&=a_xb_x\bm{e}_x\times\bm{e}_x+a_xb_y\bm{e}_x\times\bm{e}_y+a_xb_z\bm{e}_x\times\bm{e}_z\\
&\quad+a_yb_x\bm{e}_y\times\bm{e}_x+a_yb_y\bm{e}_y\times\bm{e}_y+a_yb_z\bm{e}_y\times\bm{e}_z\\
&\quad+a_zb_x\bm{e}_z\times\bm{e}_x+a_zb_y\bm{e}_z\times\bm{e}_y+a_zb_z\bm{e}_z\times\bm{e}_z\\
&=a_xb_y\bm{e}_x\times\bm{e}_y+a_xb_z\bm{e}_x\times\bm{e}_z+a_yb_x\bm{e}_y\times\bm{e}_x\\
&\quad+a_yb_z\bm{e}_y\times\bm{e}_z+a_zb_x\bm{e}_z\times\bm{e}_x+a_zb_y\bm{e}_z\times\bm{e}_y\quad(\because\bm{a}\times\bm{a}=0)\\
&=a_xb_y\bm{e}_z-a_xb_z\bm{e}_y-a_yb_x\bm{e}_z+a_yb_z\bm{e}_x+a_zb_x\bm{e}_y-a_zb_y\bm{e}_x\\
&\hspace{2em}(\because\bm{e}_x \times \bm{e}_y = \bm{e}_z, \bm{e}_y \times \bm{e}_z = \bm{e}_x, \bm{e}_z \times \bm{e}_x = \bm{e}_y,\bm{a} \times \bm{b}=-\bm{b}\times\bm{a})\\
&=(a_yb_z-a_zb_y)\bm{e}_x+(a_zb_x-a_xb_z)\bm{e}_y+(a_xb_y-a_yb_x)\bm{e}_z\\
&=\begin{pmatrix}
a_yb_z-a_zb_y \\
a_zb_x-a_xb_z \\
a_xb_y-a_yb_x
\end{pmatrix}
\end{aligned}
\\\hspace{30em}\Box
$$
最後に
今回は、大学数学・線形代数の解説記事として、ベクトルと外積について解説しました。今回は、全体でかなりの量になったので、準備も含めて書くのが大変でした。今回の内容は、内積と外積など、物理でよく登場するものです。次回は、行列の基礎とその演算の解説記事となる予定です。では。
この記事の続きは以下の記事です。
