漸化式の特性方程式（２）

前回に引き続き、漸化式の特性方程式に関して、今回は隣接3項間漸化式について考えよう。２つの解法を示そう。まず「解法１」では高校数学の範囲で、「解法２」では線型代数の理論を使って解き、それぞれ特性方程式の意味を考える。解法１での意味も解法２の観点からもう少し探ってみる。

数列a[n]（n=1,2,3,･･･)がa，b，p≠0，q≠0を定数として次を満たすとする。
　a[n+2] = pa[n+1] +qa[n]　･･･①
　a[1] = a
　a[2] = b
数列a[n]の一般項を求めよ。

解法１

Xについての２次方程式
　X^2 = pX + q
の２つの（複素数）解をα，βとする。

α，βは2次方程式の解の公式より
　α，β = { p ± √(p^2 + 4q) }/2
と求まる。

（Ⅰ）α ≠ β の場合

２次方程式解と係数の関係より
　α + β = p
　αβ = - q
を満たす。

よって、
　　a[n+2] = pa[n+1] +qa[n]
⇔　a[n+2] = (α + β)a[n+1] - αβa[n]
⇔　a[n+2] - αa[n+1] = β(a[n+1] - αa[n])　･･･②

そこで、
　b[n] = a[n+1] - αa[n]
と置けば、②は
　b[n+1] = βb[n]
であるから、これは数列b[n]が公比βの等比数列であることを意味する。

初項は
　b[1] = a[2] - αa[1]
　　　= b - αa
である。

よって数列b[n]の一般項は
　b[n] =  (b - aα)β^(n-1)
である。

即ち、
　a[n+1] - αa[n] = (b - aα)β^(n-1)　･･･③
となる。

②の変形と同様にして
　　a[n+2] = pa[n+1] +qa[n]
⇔　a[n+2] - βa[n+1] = α(a[n+1] - a[n])　･･･②’
から、
　a[n+1] - βa[n] = (b - aβ)α^(n-1)　･･･③’
を得る。

従って、③’－③でa[n+1]を消去すれば
　　(α - β)a[n] = (b - aβ)α^(n-1) - (b - aα)β^(n-1)
⇔　a[n] = {(b - aβ)α^(n-1) - (b - aα)β^(n-1)} / (α - β)　･･･④

逆に、④は元の漸化式の条件を満たす。

以上より、数列a[n]の一般項は④で表される。

（Ⅱ）α = β の場合

（Ⅰ）の③まで同じ議論ができるから、β = αとして
　　a[n+1] - αa[n] = (b - aα)α^(n-1)　･･･③’’
を得る。

ところで今、α = β = 0 なら p = q = 0となるので仮定に反するから、α ≠ 0 である。

そこで③’’で両辺α^nで割ってよく
　a[n+1]/α^n - a[n]/α^(n-1) = b/α - a
を得る。

ここで
　c[n] = a[n]/α^(n-1)
とおけば上の等式は
　c[n+1] - c[n] =  b/α - a（定数）
となるから、数列c[n]は公差b/α - aの等差数列であり、初項は
　c[1] = a[1]/α^(1-1)
　　　= a
である。

よって、
　c[n] = a + (n - 1)(b/α - a)
である。

即ち、
　a[n]/α^(n-1) =  a + (n - 1)(b/α - a)
である。

よって、
　a[n] = {a + (n - 1)(b/α - a)}α^(n-1)
　　　= (2a - b/α)α^(n-1) + n(b/α - a)α^(n-1)　･･･④’

逆に、④’はもとの漸化式を満たす。

以上より、数列a[n]の一般項は④’で表される。

特性方程式の意味

さて、解法の冒頭から突然、２次方程式
　X^2 = pX + q
を考えた。その理由は②式
　a[n+2] - αa[n+1] = β(a[n+1] - αa[n])　･･･②
に変形したいことにあった。

この２次方程式をもとの漸化式①に対する特性方程式という。

特性方程式を手掛かりに、①から②へうまく変形している。

大学入試の記述式試験の際は、特性方程式のことは書かず直接①⇔②、即ち
　　a[n+2] = pa[n+1] +qa[n]
⇔　a[n+2] - αa[n+1] = β(a[n+1] - αa[n])
と同値変形で記述すればよい。実際、”嘘”ではないのだから。

この特性方程式を考える意味は、上記の説明で理屈は通るが、２次方程式を手掛かりにするというのは背景に一体何があったのだろうか。

次に線形代数の理論を使って解いてみよう。このとき特性方程式は自然に現れる。

線型代数は通常の高校カリキュラムでは習わない領域であるが、線型代数の一般論はここでは詳説しない。

解法２（その１：準備）

まず複素数列全体の集合をＳとおく。なお、aが複素数列であるとは、自然数nに対して複素数a[n]が対応している写像である。

複素数体をℂで表す。

Sの上には和(+)：
　(a + b)[n] = a[n] + b[n]，a,b∈S
とスカラー倍(・，または演算記号を省略する)：
　(α・a)[n] = αa[n]，α∈ℂ,a∈S
が定義され、これらによってＳはℂ上の線型空間となる。

Sの任意の元aを
　a ↦ (a[1],a[2],･･･,a[n]，･･･)，a[i]∈ℂ
によって対応づけることで、ℂ^∞と同型であることがわかる：
　S≅ℂ^∞

次に、与えられた漸化式
　a[n+2] = pa[n+1] +qa[n]　･･･①
を満たす複素数列すべての集合をＶと置く。ここでは
　a[1]，a[2]
の値（初期条件）は固定せず、単に①を満たす数列の全てを考えて、その集合をＶと定義している。

VはSの部分集合であるが、VはSの和とスカラー倍について閉じている。従って、VはSの部分線型空間である。

Vの任意の元aは、漸化式①によって初めの２項a[1]，a[2]が決まれば数列aが一意的に定まることから
　a↦(a[1],a[2])
の対応により、Vはℂ^2と同型である：
　V≅ℂ^2

さて、一般に与えられた数列a∈Sに対して、番号をひとつずらしてできる新しい数列a'を考える。つまり、
　a = (a[1],a[2],a[3],a[4],･･･)
のとき、
　a' = (a[2],a[3],a[4],a[5],･･･) 
を考える。

これは数列全体の集合SからS自身への写像であるが、ここではこれを「ずらし写像」と呼ぼう。（一般的な用語ではないので注意）

ずらし写像は和とスカラー倍を保つゆえ、SからSへの線形写像である。

なお、自分から自分への線形写像を特に自己準同型という呼ぶ。（準同型はここでは線型空間を考えているから、線形写像を意味する。）ずらし写像はS上の自己準同型である。

さらにaが漸化式①を満たすときに、こうしてできる数列a'はまた漸化式①を満たす。つまり
　a∈V　⇒　a'∈V
である。

よって、この対応
　a↦a'
はＶ上に制限して考えれば、V上の自己準同型と考えてよい。

今、このV上の自己準同型を記号で
　F : V→V
とおこう。

解法２（その２：固有多項式）

さて、ずらし写像Fの固有値αに対する固有ベクトルxとは
　F(x) = αx
を満たすこと、即ち数列xが公比αの等比数列であることを意味する。

従って、固有ベクトルは等比数列であり明示的に一般項が記述できる。そこでFの行列表示がジョルダン標準形となるような、Vの基底を求めれば、数列の一般項が完全に記述できるという訳である。

まず、Fの固有多項式P(X)を求めよう。

実際、Vとℂ^2の同型対応により、ℂ^2の自然基底（単位ベクトルの組み）：

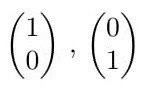
に対応するVの基底に関するFの行列表示Aを求めると

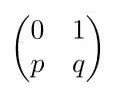
となり、Fの固有多項式：
　det(XI - A) = X^2 - pX - q
を得る。

解法２（その３：一般項）

次にFの固有多項式
　Φ(X) = X^2 - pX - q
の根をα，βとおき、
　Φ(X) = (X - α)(X - β)
を考える。
（Φ(X)は代数学の基本定理よりℂの範囲で重複を含めて２つの根をもつことがわかっている。）

（Ⅰ）α≠βの場合
Fは相異なる固有値α，βを持つからFを行列表示したときのジョルダン標準形は

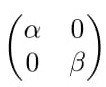
であり、
　V = Ker(F - αI) ⊕ Ker(F - βI)
と２つの０でない部分空間の直和に分解される（固有空間分解）。

そして、
　　x∈Ker(F - αI)
⇔　(F - αI)x = 0
⇔　F(x) = αx
⇔　x[n+1] = αx[n]（任意のn=1,2,3,･･･について)
⇔　x∈<(α^(n-1))>
（ここで、(α^(n-1))とは、第n項がα^(n-1)となる数列を表し、<a>はVの元aで生成される部分空間とした。）
であるから、Vは次の２つの元の組を基底にする：
　(α^(n-1))，(β^(n-1))
（これらは一般項が明示的な数列である）

よって、初めの漸化式①を満たす任意の数列a∈Vは、これらの一次結合で一意的に表される：
　a = C・(α^(n-1)) + D・(β^(n-1))，C,D∈ℂ　･･･(1)

特に、初期条件が与えられたとき、つまり
　a[1] = a，a[2] = b
のとき、(1)式より
　a = C + D
　b = Cα + Dβ
を満たす複素数C,Dが決定され、
　C = (b - aβ) / (α - β)
　D = - (b - aα) / (α - β)

よって、一般項は
　a[n] = {(b - aβ)(α^(n-1)) - (b - aα )(β^(n-1))} / (α - β)
と求まる。

この解は、上の「解法１」で求めた解④と確かに一致している。

（Ⅱ）α=β の場合
q≠0よりα≠0である。Fは固有値α≠0のみを持つが、（Ⅰ）でみたように
　　x∈Ker(F - αI)
⇔　x∈<(α^(n-1))>
つまり、
　Ker(F - αI) = <(α^(n-1))>
である。

よって　
　dim Ker(F - αI) = 1
となる。

このこととFの固有多項式が
　Φ(X) = (X - α)^2
より、Fを行列表示したときのジョルダン標準形は

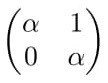
となる。

よって、e,fをℂ^2の自然基底に対応するVの基底とすると
　(F - αI)(e) = 0　･･･(2)
　(F - αI)(f) = e　･･･(3)
である。

(2)式よりある定数E∈ℂを用いて
　e = E・(α^(n-1))
がわかり、(3)式より
　　F(f) - αf = e
⇔　F(f) - αf = E・(α^(n-1))
⇔　F((f[n]/α^(n-2))) - (f[n]/α^(n-2)) = E・(1)
⇔　(f[n]/α^(n-2)) = E・(n)
⇔　f = E・(n・α^(n-2))

よって、Vの基底として（スカラー倍を適当に調整して）
　(α^(n-1))，(n・α^(n-1))
が得られた。（これらは一般項が明示的な数列である）

よって、初めの漸化式①を満たす任意の数列a∈Vは、これらの一次結合で一意的に表される：
　a = C・(α^(n-1)) + D・(n・α^(n-1))，C,D∈ℂ　･･･(4)
の形に一意的に表される。

特に、初期条件が与えられたとき、つまり
　a[1] = a，a[2] = b
のとき、(4)式より
　a = C + D
　b = Cα +2Dα
を満たす複素数C,Dが決定され、
　C = (2aα - b) / α
　D = (b - aα) / α

よって、一般項は
　a[n] = {(2aα - b)(α^(n-1)) + (b - aα )n(α^(n-1))} / α
　　　=  (2a - b/α)α^(n-1) + n(b/α - a)α^(n-1)
と求まる。

この解は、上の「解法１」で求めた解④’と確かに一致している。

解法２での補足事項（自己準同型環）

ここで補足事項として１つの観点に注目しよう。解法２のロジックに影響はないが、この観点が解法１の特性方程式に意味合いをより強く見せると考えるため触れておきたい。

ずらし写像F : V→Vを使えば、漸化式①を満たす任意の数列a∈Vとは、次の等式を満たす数列aとして特徴づけられる：
　F^2(a) = pF(a) - qa
即ち、
　(F^2 - pF - qI)(a) = 0　･･･（注意１）

（注意１）
ここで、自己準同型全体の成す集合に、「和」と「ℂ上のスカラー倍」を値による演算：
　(f + g)(x) = f(x) + g(x)
　(α・f)(x) = αf(x)
　（f,g：自己準同型，α∈ℂ，x∈Ｖ）
で定め、「積」を写像の合成：
　fg = f◦g
によって定義することができ、従って自己準同型全体はℂ上の線型空間であり、かつ環の構造をもつ。これを自己準同型環と呼ぶ。
例えばF^2とはFを２回合成してできる自己準同型：
　F^2 = F◦F
である。また、Iは恒等写像：
　I(x) = x
となる。
（注意１終わり）

よって自己準同型
　F^2 - pF - qI
はVの上で零写像（任意のVの元を0に写す線型写像）である。

多項式P(X)を
　P(X) = X^2 - pX -q
とおくと、上記の自己準同型はP(X)にFを「代入」したものである：
　P(F) = F^2 - pF - qI

従って、P(F)がVの上で零写像であるとは、
　V = Ker P(F)
ということである。

（なお、解法２では先にFの固有多項式Φ(X)を求めたが、これは上のように定義したP(X)と一致している。）

特性方程式の意味（線型代数の観点）

解法２より、特性方程式はずらし写像Fの固有多項式Φ(X)を使って
　Φ(X) ＝０
の形となって現れている。

解法２のジョルダン標準形の理論に持ち込む上ではこの認識は重要であるが、解法１の特性方程式の計算が意味していることは、もっと直接的である。

特性方程式はΦ(X)の意味よりも、上記の補足事項で説明したところのP(X)の意味で捉える方がもっと直接的であると考える。

従って、特性方程式：
　X^2 - pX - q = 0
は、
　F^2 - pF - qI = 0
という、自己準同型環の上での計算に他ならない。

例えばケース（Ⅰ）の場合で
　　a[n+2] = pa[n+1] +qa[n]
⇔　a[n+2] - αa[n+1] = β(a[n+1] - αa[n])
という計算は、
　　F^2 = pF + qI
⇔　F^2 - αF = β(F - αI)
という計算に他ならない。

参考図書

一般に与えられた自己準同型fのジョルダン標準形の理論やそれを求める方法の説明はここでは割愛した。なお、初めて線型代数やジョルダン標準形を学習するのに分かりやすい参考図書として以下がある。また、本記事の「ずらし写像」という用語は[1]から拝借した。

[1]　線型代数入門，松坂和夫，岩波書店
[2]　Jordan標準形と単因子論Ⅰ，Ⅱ，杉浦光夫，岩波書店