タイル張り

縦と横が「２×１」または「１×２」の形のドミノをいくつか使って、図のような「８×８」の枠の中に升目に沿って隙間なく敷き詰めてみよう。

これは難なく敷き詰められるだろう。

では、この枠の１つの対角線にある角２つを取り除いた枠の中に、ドミノを隙間なく敷き詰めることはできるだろうか。

ドミノは面積が２だから敷き詰められるとしたら、面積が偶数でなければならない。そして上の例はもともと「８×８」の形をした枠であり、そこから角の２つを取り除き、面積は６４－２＝６２で偶数である。

６２ということは３１枚のドミノで敷き詰められるかもしれない。

しかしやってみるとどう頑張っても敷き詰められないようである。

もしかしたら敷き詰めることはできないのではないかという気がしてくる。

もしそうなら、なぜ敷き詰められないのだろう。

よく知られた敷き詰められないことの証明には、８×８の枠を市松模様（２色の色を使って交互にマスを塗り分けてできる模様）に「塗り絵」してみるとそれが見えて来るという。

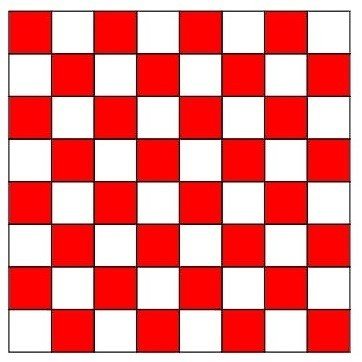
２色を紅白としたら、「８×８」の枠を市松模様に塗るとき、白は３２個、赤も３２個ある。

ところでドミノを升目に沿って好きなところへ１つ敷こうとすると、市松模様の効果で、赤と白がちょうど１つずつ塗られた場所に敷くことになる。

よって、もし完全に敷き詰められるとしたら、白の数と赤の数が同数でなければならないことになる。

１つの対角線にある角２つを取り除いた枠には、同じ色が２色消えて、同数にならない。

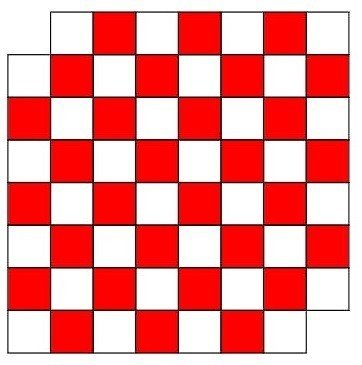
よって、この形にドミノを敷き詰めることは不可能であることが証明された。

この方法を知らなくて思いついた人はすばらしい！

形を変えればいくらでも問題は作れるが、一般には総称して「タイル張り問題」といわれる。

こういうタイル張りできたとしたときに成り立つ性質を見抜いて、不可能性が証明されるのは威力がある。

升目が偶数必要だというのも、ドミノ張りの必要条件だが、この問題ではそれだけでは及ばず、それよりも強い条件を見出せるかというのがポイントになってくる。