
利息計算から生まれた超越数
高校数学において、指数関数などの項目で登場する e という数があります。「自然対数の底」と呼ばれるものです。回りくどい言い方ですね。実は、数そのものにもちゃんと名前があり、「ネイピア数」といいます。(高校では「ネイピア数」という名前自体は教わらなかったかもしれません。)
この数の定義は、
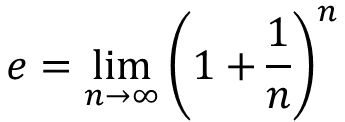
という式で定義されます。
学校では唐突にこの式が登場し、そして、頭ごなしに「覚えろ」と言われ、大抵の場合、なぜこの形なのかということについての説明はありません。
指数関数ではこれなしには始まらないほど重要な数ですし、科学の分野でも欠くことのできない存在である反面、学校でのこういう頭ごなしの教え方ってあんまりだと思います。
という訳で・・・
ネイピア数。いきなり登場するこの複雑な定義式は一体何なのか、この記事で掘り下げていこうと思います。
(軽い気持ちで書こうと思いたちましたが、調べてみると何とも・・・奥が深かったです。)
始まりは利息の計算から
ネイピア数は非常に奥が深く、数学や科学分野に不可欠の重要な定数です。そんなネイピア数ですが、その始まりは意外にも科学の分野ではなく、金融の分野なのです。
お金の貸し借りには利息が生じます。大抵の場合は、複利方式での計算、つまり利息の計算の際、以前に生じた利息を元本に加えて計算する方式を取ります。
例えば、10000円を年利率100%で借りた場合(!!!・・・普通はありえないぼったくり利率ですが、計算の内容を簡単にするため)、返済がなければ初年の利息は10000円です。
利息(1年目)=10000×100%=10000
複利方式では、この利息分が元本に組み入れられるので、2年目の利息は10000円ではありません。元本が10000+10000(←利息)=20000となり、よって、2年目の利息は、20000×100%=20000円となります。これが複利計算の方法です。
利息(2年目)=20000×100%=20000
複利方式が恐いのは、利息がどんどん大きくなるので、最初は少額だった借金がいつの間にか巨額に膨れ上がる可能性がある点ですね。
さて、ここまで借金の目線で利息を論じましたが、もう少しポジティブな話題に切り替え、ここからは、預金で利息を考えてみることにしましょう。
同じく年利100%で預けられる預金があったとします(本当にあったら全財産預けたいところです!)。1万円借りるではなく、1万円預金することを考えます。この時、1年間資産の増え方をグラフにするとこんな感じになります。
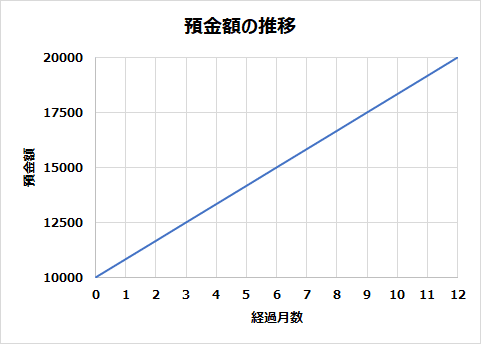
ただし、これは1年間預けっぱなしならということです。実はもっとリターンを増やす方法があります。途中で利息も含め預金を全額引き出し、もう1度預金し直すのです!
例えば、半年たった時点で一度全額引き出す。1年の利率100%に対して、半年の利率は、1年に対して期間が半分になるから、100%を2分の1で50%。上のグラフからも分かるように、元本の1万円の50%である5千円の利息が付き、預金額は1万5千円になっているのが分かります。
半年の時点でいったん全額(10000[元本]+5000[利息]=15000)を引き出し、それを再び全額預金したらどうなるか。グラフはこうなります。
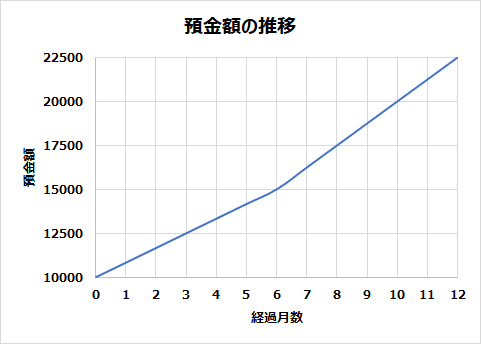
なんと!リターンが増えました。1年預けっぱなしの時と、結果を数式で比較するとこんな感じになります。
1年預けっぱなし:10000×(1+1)=20000・・・(1)
半年時点で元本組入れて預金:10000×(1+0.5)(1+0.5)=22500・・・(2)
1+1というのがすぐに腹落ちしない方のために補足しておきますと、
利率なし(0%)だったら元本は変わらない(1倍)。利率100%というのは、貸出額と同額が利息になるということだから、元本自体(1倍)に利息100%(これも元本の1倍)が乗り、満期に受取が1+1=2倍になるということになりますよね。
つまり元本に対し、(1+利率)をかけてやると、引き出し時の受取額になるということです。
リターンを最大化するには?
この結果を見て、すぐにあることに気付くと思います。もっと短い期間で、
【預金引き出し→利息を元本に組み入れて預金】
を繰り返せば、もっとリターンが大きくなるのでは?
例えば、四半期(3ヶ月)ごとに【引き出し⇔預金】を繰り返したらどうなるでしょうか?3ヶ月時点の利率は25%で、その利息組入れ預金を4回繰り返すから、
四半期で元本組入れて預金:
10000×(1+0.25)(1+0.25)(1+0.25)(1+0.25)≒24414
おお、増えた!・・・あれ?
・・・増えはしたけど、さっきほど増加量が少なくなったような・・・。もしかしたら、無限に組み入れ期間を細かくしたら(それこそ1秒ごととか)、無限に利息が増える期待もあったかもしれませんが、その期待は外れそうです。組み入れ期間の分割数と投資の報酬(貸出額が何倍になるか)の関係をグラフにすると、こんな感じになります↓
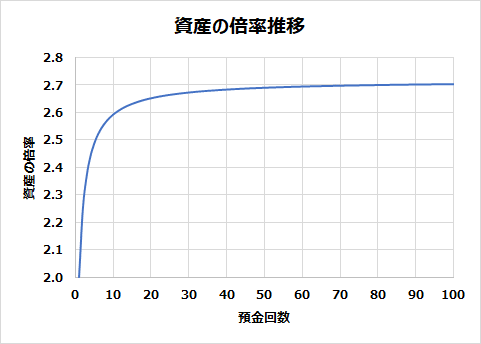
組み入れ期間を極限まで短くすれば、リターンは確かに多くなりますが、無限に膨れ上がるわけではなさそうですね。最初の1,2回はあっさり2000円以上リターンが増えていたのに一体何が起こっているのでしょうか。グラフの最右端、1年間の間に【全額引き出し→元本を組み入れて再預金】を、100回繰り返す場合の預金額を、数式で表して調べてみましょう。この辺はもう、ほとんど組み入れ回数を増やしても意味がないくらい平らになってます。
1回の期間が1年の100分の1になるので、その利率は100%÷100=1% この利率で100回、【全額引き出し⇔全額預金】を繰り返す。なので満期の受取額は、
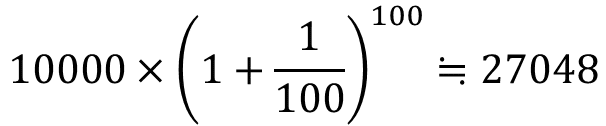
( )の中身は、1+0.01=1.01です。ほとんど1です。半年後に1度だけ利息の組み入れをした(1)式の時の( )の中身は、1+1=2でした。なるほど、ほとんど1のものを何回もかけ合わせているわけなので、その回数が1,2回変わっても、ほとんどリターンが変わらないのはうなずけますね。
このグラフを見るに、組み入れ回数を増やせば、100回以降も多少は増えそうですが、上限がありそうです。では、その上限とはどんなものでしょうか。無限回利息組入れをした場合というのを考えてみましょう。もうそれこそ、0.000…1秒ごとに【全額引き出し⇔全額預金】を繰り返すイメージです。
もはや人間ワザではありませんが、思考実験です。
計算式を作るにあたり、まず再預金の回数をn回と一般化して考えます。1回の預金の期間が1年のn分の1になるので、その利率は100÷n% この利率をn回かける。すると満期の受取額は、
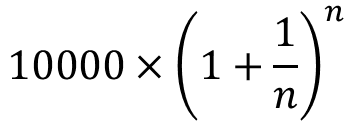
ということになります。
無限回繰り返すということは、このn回というのが無限回になる、ということです。数学ではこれを lim という記号で表現します。つまりは、
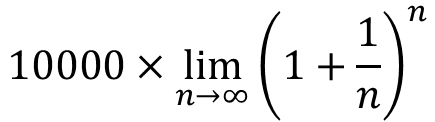
となります。
さて、お気づきでしょうか?満期受取額の当初元本に対する倍率が、最初に示したネイピア数の定義そのものになっています。つまり年利100%の融資を、利息組み入れ回数を極限まで大きくした場合の行き着く先は、
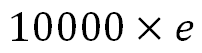
となるということです。e はネイピア数を表す記号です。ちなみに、このネイピア数は、e=2.71828182846・・・と続く無理数の一つです。
無限に【全額引き出し⇔全額預金】を繰り返しても、最初の元本10000円に対して、e 倍以上に増やすことはできないということが分かります。
ネイピア数の由来と発見者
この真理は、17世紀スイスの数学者、ヤコブ=ベルヌーイによって見いだされました。因みにベルヌーイ家は数々の天才数学者、科学者を生んだ血筋です。(画像はwikipediaから引用)

ヤコブ=ベルヌーイ
では、「ネイピア数」という名前はどこから来たかというと、16世紀スコットランドの貴族、ジョン=ネイピアにちなんでいます。この人は、本記事で紹介した複利計算からネイピア数を発見したわけではありませんが、対数の研究の中で、ネイピア数の近似値を計算した記録が残っています。(これもWikipediaから引用)

ジョン=ネイピア
世界最古の発見者の名にちなんでネイピア数と名付けられたということですね。
