モーションにおける3次元回転 #5 〜ロドリゲスの式の幾何学的意味〜
前章「モーションにおける3次元回転 #4」で,3次元回転を表すロドリゲスの式について述べたが,これは2次元平面の回転を複素数で表すオイラーの公式から単位クォータニオンへの橋渡しと位置づけていたが,もう少し補足する.
復習
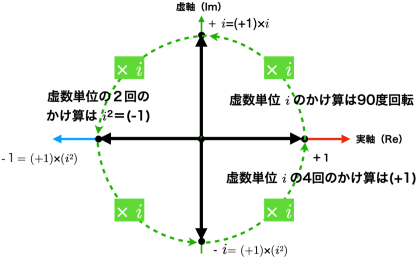
図1のように,複素平面で虚数$${i}$$をかけることは,複素平面上の原点まわりの回転を意味する.
例えば,図1の実数軸上の一番右の点である$${1}$$に「虚数 $${i}$$ をかけること」で,$${1 i =i}$$となり単位円上の一番上の点にの移動する.これは複素平面では「単位円上を90度回転すること」に相当する.試しに,もう一度 $${i}$$ をかけると「$${-1}$$」になる($${i * i =-1}$$).つまり,$${i}$$ をかけることは複素平面の単位円上をさらに90度回転することになっていた.
また,オイラーの公式
$$
e^{i \theta}=\cos \theta + i \sin \theta
$$
は,さらに複素平面の単位円上の回転を一般化し,単位円上の点は,偏角$${\theta}$$を利用すれば,実部の$${\cos \theta}$$と,虚部の$${\sin \theta}$$で表現できた.
つまり,平面の回転は「複素数」で,さらに指数表現の「オイラーの公式」で単位円上の回転を表すことができた.つまり,虚数をかけることで90度の回転を実現し,オイラーの公式によって任意の角度$${\theta}$$も表現できる.
そこで,次に同じことを3次元空間の回転で実現することを考えることになるが,課題は,
・3次元空間における虚数に相当するものは?
・3次元空間の単位球上の回転をどのように表現するのか?
になる.
そして,そのヒントとなるのがロドリゲスの式
$$
\bm{R}(\psi) = \bm{E} + [\bm{n} \times ] \sin \psi + [\bm{n} \times ]^2(1- \cos \psi)
$$

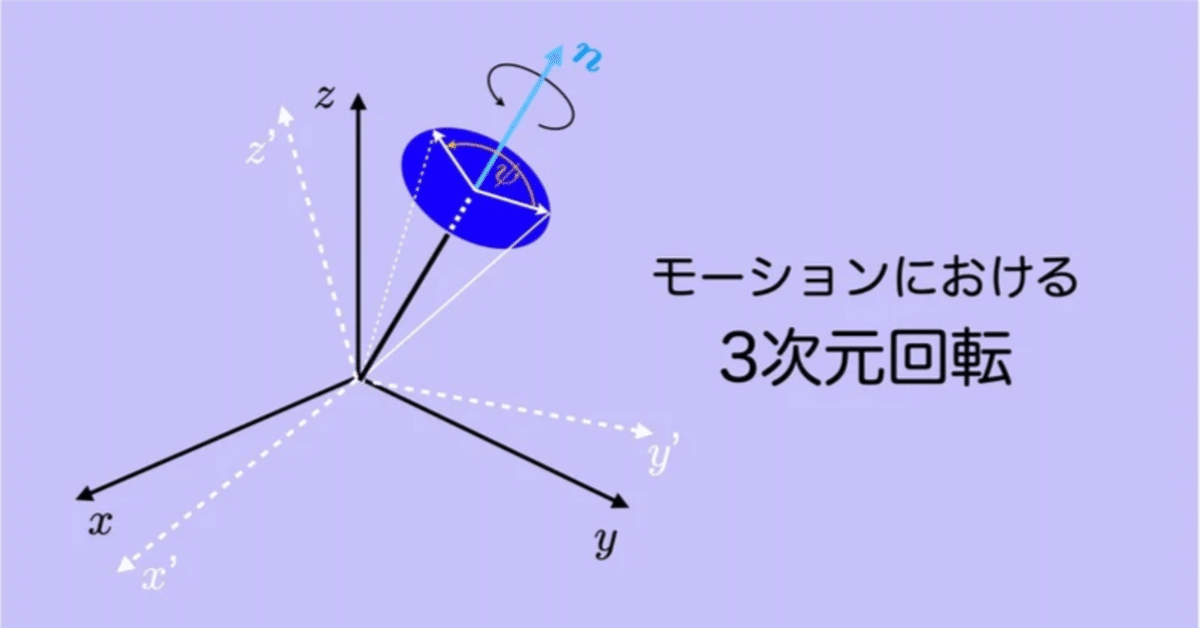
であった.ロドリゲスの式は複素平面のベクトルの回転と同様,任意の3次元空間上のベクトルの回転を原点を通る任意の回転軸$${\bm{n}}$$と角度$${\psi}$$として与えた(図2).
ロドリゲスの式は回転行列$${\bm{R}}$$を表す式であるから,任意のベクトル$${\bm{a}}$$にこれをかければ,ベクトルは回転し新しい位置ベクトル$${\bm{a}'}$$となり(図2参照),
$$
\bm{a}'=\bm{Ra} = \bm{a} + [\bm{n} \times ] \bm{a} \sin \psi + [\bm{n} \times ]^2 \bm{a}(1- \cos \psi)
$$
と書くことができるが,この式の右辺第1項の$${\bm{a}}$$は原点から,回転する平面への移動($${\overrightarrow{OP}}$$)を意味するので,あとはこの平面上での回転を考えればよい.これは複素平面での回転と似ている.
また,この式の右辺の第2項の$${[\bm{n} \times ] \bm{a}}$$はベクトル$${\overrightarrow{QR}}$$を指し,$${\sin \psi}$$をかけることで右辺の2項は$${\overrightarrow{HP'}}$$を意味している.
さらに,この式の右辺の第3項の$${[\bm{n} \times ]^2}$$はベクトル$${-\overrightarrow{PQ}}$$を指し,$${1-\cos \psi}$$をかけることで右辺の第3項は$${\overrightarrow{PH}}$$を意味している.
では,2次元平面の回転の虚数に相当するものを探すために,オイラーの公式の右辺
$$
\cos \theta + i \sin \theta
$$
と,ベクトル$${\bm{a}}$$による回転平面に移動後に相当する,ロドリゲスの式の第2,3項
$$
[\bm{n} \times ] \sin \psi + [\bm{n} \times ]^2(1- \cos \psi)
$$
を見比べると,全く同じではないが,2次元回転の虚数$${i}$$は,3次元回転では$${[\bm{n} \times ]}$$に相当するのでは?と予感させる.
外積[n x]の幾何学的意味
復習が長くなってしまったが,ここではロドリゲスの式における外積$${[\bm{n} \times ]}$$の幾何学的意味を考える.

ここで,前章「モーションにおける3次元回転 #4」で述べた外積の性質から,図3の単位ベクトル$${\bm{n}}$$とベクトル$${\bm{a}}$$の外積$${\bm{n} \times \bm{a} =[\bm{n} \times ] \bm{a}}$$は,$${\bm{n}}$$と$${\bm{a}}$$の張る平面の法線方向(に垂直な方向)を向く.また,$${\bm{n}}$$が単位ベクトルであることを考えると,この外積は$${\bm{a}_0}$$と同じ大きさの$${\bm{a}_{1}}$$となり,これは$${\bm{a}_{0}}$$を軸$${\bm{n}}$$まわりに90度回転させたベクトル$${\bm{a}_{1}}$$に相当する.
さらに,$${[\bm{n} \times ]^2 \bm{a}=[\bm{n} \times ][\bm{n} \times] \bm{a}}$$は,単位ベクトル$${\bm{n}}$$と$${[\bm{n} \times] \bm{a}}$$の外積,すなわち$${\bm{n}}$$と$${\bm{a}_1}$$との外積であるから,前の$${[\bm{n} \times ] \bm{a}}$$の外積と同様に,幾何学的に$${\bm{a}_{2}}$$となり,これは$${\bm{a}_{1}}$$を軸$${\bm{n}}$$まわりに90度回転させたベクトルである.
同様に,さらにもう一度$${[\bm{n} \times] \bm{a}}$$をかけた$${[\bm{n} \times]^3 \bm{a}}$$は$${\bm{a}_{2}}$$を90度回転させた$${\bm{a}_{3}}$$のベクトルに,$${[\bm{n} \times]^4 \bm{a}}$$は$${\bm{a}_{3}}$$を90度回転させた$${\bm{a}_{0}}$$に戻る.
このように,$${[\bm{n} \times]}$$をかける操作は,幾何学的には図4の円上を$${\bm{n}}$$まわりに90度ずつ回転させる操作であることがわかり,2次元平面の回転における虚数$${i}$$とまったく同じ役割を果たしている.
[nx]^nの導出
前節では外積$${[\bm{n} \times]}$$の意味を幾何学的に示したが,次に,このことを式で示す.前章「モーションにおける3次元回転 #4」のベクトル三重積の結果から
$$
[\bm{n}\times]^2= \bm{nn}^T -\bm{E}
$$
となり,
$$
[\bm{n}\times]^3= (\bm{nn}^T −\bm{E})[\bm{n}\times]=\bm{nn}^T[\bm{n}\times]−\bm{E}[\bm{n}\times]=−[\bm{n} \times]
$$
となり,
$$
[\bm{n}\times]^4= (\bm{nn}^T −\bm{E})(\bm{nn}^T −\bm{E})=-(\bm{nn}^T −\bm{E})=-[\bm{n}\times]
$$
を得る.なお,$${\bm{n} \times \bm{a}}$$は反射影$${\bm{a}_{\perp}=(\bm{E}-\bm{nn}^T)\bm{a}\equiv\bm{P}_{\perp}\bm{a}}$$と一致する.
以上まとめると,
$$
~[\bm{n}\times]^1=[\bm{n}\times]=\bm{P}_{\perp}\\ ~[\bm{n}\times]^2= \bm{nn}^T -\bm{E}\\ ~[\bm{n}\times]^3=−[\bm{n} \times]\\~[\bm{n}\times]^4=-[\bm{n}\times]^2
$$
となる.
なお,ベクトル$${\bm{a}}$$に対して$${[\bm{n}\times]}$$をかけることは,図3の円上でベクトル$${\bm{a}_0}$$を90度ずつ回転することに相当しているように,これは虚数について,
$$
i^1=i\\i^2=-1\\i^3=-i\\i^4=1
$$
が成り立ち,複素平面で同様に90度ずつ回転していることと似ている.
以上の結果,冒頭で述べたように,$${[\bm{n}\times]}$$を任意のベクトルにかけることは,複素平面における虚数と同様に,3次元空間における軸$${\bm{n}}$$まわりのベクトルの回転であることが示された.
ロドリゲスの式の指数表現
実は,オイラーの公式の2次元平面の回転は,3次元空間にも拡張でき,ロドリゲスの式も指数関数表現ができ,
$$
e^{[\bm{n}\times]} = \bm{E} + [\bm{n} \times ] \sin \psi + [\bm{n} \times ]^2(1- \cos \psi)
$$
が成り立つ.導出は,参考文献1), 2)などを参考にするとよいが,基本的にオイラーの公式と同様である.以上よりロドリゲスの式は
$$
\bm{R}_{\bm{n}}(\psi)=e^{[\bm{n}\times]} = \bm{E} + [\bm{n} \times ] \sin \psi + [\bm{n} \times ]^2(1- \cos \psi)
$$
と書くことができ,オイラーの定理(剛体の回転は,回転軸$${\bm{n}}$$まわりの,回転角度$${\psi}$$の回転で表すことができる)となっている.
ロドリゲスの式の注意点
なお,オイラーの公式
$$
e^{i \theta}=\cos \theta + i \sin \theta
$$
は常に,このように記述されるが,ロドリゲスの式は複数の記述方法があり,それは幾何学的には通り道(例えば,$${\overrightarrow{OQ}, \overrightarrow{QP}, \overrightarrow{PH'}}$$等)によって異なることに由来するが,それらは等価である.教科書によって記述方法が異なるが,本稿ではオイラーの公式の3次元版を意識した記述方法となっている.
ロドリゲスの式から単位クォータニオンへ
準備が長くなってしまったが,これらの3次元空間における回転の幾何学的意味を踏まえ,次章で単位クォータニオン(オイラーパラメータ)を導入する.
参考文献
1.ロボットモーション(岩波講座ロボット学2),内山勝・中村仁彦著,岩波出版
2.ヒューマノイドロボット(改訂2版),梶田秀司 編著,オーム社

【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
