
動かして学ぶバイオメカニクス#6 〜多関節構造のニュートンの運動方程式〜
身体の逆動力学計算は,ニュートンの運動方程式とオイラーの運動方程式を再帰的に解く作業である.これまでの記事で,そのうちニュートンの運動方程式を解く逆動力学解析の準備が整った.ここでは,さらにフォースプレートのデータを取り込むなどの,いくつかの修正を加えて.全身の力学計算のうちニュートンの運動方式の計算を完成させる.
外力としての床反力
全身運動で地面や外部環境との力の相互作用がある場合,それらは「外力」として扱われる.もし地面とだけ接している場合,ニュートンの運動方程式では床反力(地面反力)が唯一の外力となる.
第4章
でも述べたように,モーションキャプチャなどで全身計測が可能な場合,床反力は重心の加速度からも推定が可能だが,実際には筋肉や関節などの粘性の影響や,左右の脚に作用する力を分離できないなどの課題も多く,直接床反力を計測し,力学計算に取り込むのが通常である.
第4章で示したように,全身のニュートンの運動方程式は
$$
\sum_{i=1}^{n} (m_i (\ddot{\bm{x}}_{gi} - \bm{g})) = \bm{F} \\
M(\ddot{\bm{X}}_{G} - \bm{g}) = \bm{F}
$$
となる.ここで,$${m_i}$$は身体の部位$${i}$$の質量,$${\bm{x}_{gi}}$$は部位$${i}$$の重心の位置ベクトル,$${\bm{g}}$$は重力加速度,$${\bm{F}}$$は床反力,$${M=\sum_{i=1}^n m_i}$$は全身の質量(体重),$${\bm{X}_{G}}$$は身体重心の位置ベクトルである.
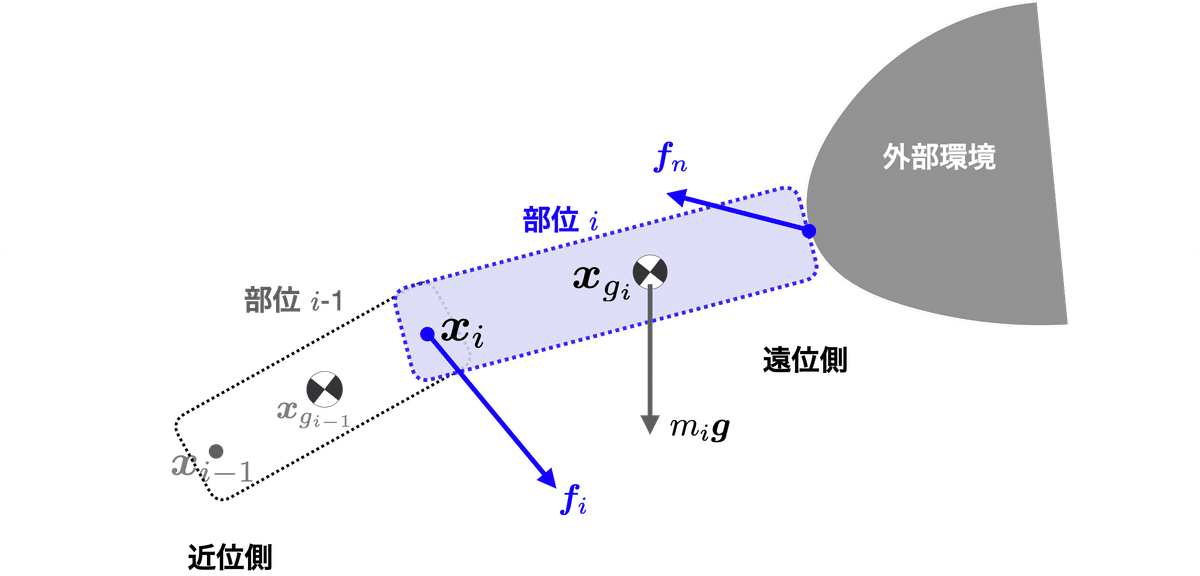
また,図1のように地面や外部と接する部位のニュートン運動方程式は,
$$
m_i (\ddot{\bm{x}}_{gi} - \bm{g})= \bm{f}_i + \bm{f}_n
$$
と書くことができ,外力(たとえば床反力)$${\bm{f}_n}$$を計測すれば,部位$${i}$$に作用する力$${\bm{f}_i}$$を解くことができる.なお,ここで$${\bm{f}_n}$$は部位$${i}$$に作用する力として定義されているので,力ベクトルの定義に注意されたい.
このように,外部環境と相互作用のある部位に作用する力も,再帰的に取り込むことができるので,全身の運動方程式を第4章のコードを大きく変更することなく,計算できる.
また,床反力以外に外部環境と相互作用がある場合は,その部位の力計測を加えればよいだけである.ただしモーションキャプチャの座標系に座標変換が必要であるので注意されたい.
全身の並進運動方程式の解き方
第4章のコードに,床反力の取り込みと,前章
の平滑化スプラインを用いた重心の加速度計算を組み入れて,全身のニュートンの運動方程式の計算を完成する.
なお,コードは,これまで同様に,以下のGoogle Colaboratoryのリンクから,ブラウザでPythonコードを実行できるようにした.なお,ログインするためには,Googleアカウントが必要となるので注意をされたい.
また,後半で使用するモーションキャプチャのサンプルデータ(sample_optitrack_221027.csv)と,フォースプレートのサンプルデータ(sample_fp_221027.csv)は,このリンクからダウンロードして,Google Driveをマウントし,マウントしたドライブにそれらをコピーしてご使用いただきたい.
なお,データは台からの飛び降り着地動作で,片足(右脚)で着地してバランスを取るタスクのデータである.フォースプレートは2台計測し,左足の床反力データは取りこんでいるが,力データはほぼ0を返すだけである.
床反力データの取得
以下のように,Pythonのpandasを利用し,フォースプレートの床反力データ(csvファイル)を取り込み,力とモーメントのデータを,フォースプレートの番号(fp_num:1→左,2→右)と,力か力のモーメント(fp_type:'f'→力,'m'→力のモーメント)を指定し,関数extract_fp_vec()で抽出する.これはモーションキャプチャの位置ベクトルと同様に,3次元のベクトル(n x 3の2次元配列:nデータ数)で出力する.
# Force PlateのCSVデータから指定したchのデータを抽出
# ファイル名とchの名前を引数に与えて力または力のモーメントを抽出する関数
# fp_num:1 or 2(1: 左,2:右)
# fp_ch:'Fx', 'Fy', 'Fz', 'Mx', 'My', 'Mz',から選択
def extract_fp(file_path_fp, fp_num:int=1, fp_ch:str='Fx'):
df = pd.read_csv(file_path_fp, skiprows=[0,2,3,4,5])
fp_name_list = np.unique([x[0:4] for x in df.columns[1:]]) # force plateの名前のリストを抽出
header = fp_name_list[fp_num-1] + '-' + fp_ch
# force plateの座標をmotion captureの座標に変換し出力
if fp_ch == 'Fx' or fp_ch == 'Mx':
return -df[header].values
else:
return df[header].values
# forceとmomentのベクトルとして出力
# fp_num:1 or 2 (1: 左,2:右)
# fp_type:'f', 'm',から選択('f':force,'m':moment)
def extract_fp_vec(file_path_fp, fp_num:int=1, fp_type:str='f'):
if fp_type == 'f':
return np.array([extract_fp(file_path_fp, fp_num, 'Fx'), extract_fp(file_path_fp, fp_num, 'Fy'),
extract_fp(file_path_fp, fp_num, 'Fz')]).T
elif fp_type == 'm':
return np.array([extract_fp(file_path_fp, fp_num, 'Mx'), extract_fp(file_path_fp, fp_num, 'My'),
extract_fp(file_path_fp, fp_num, 'Mz')]).Tまた,フォースプレートとモーションキャプチャのサンプリングレートが異なるので,前章で述べたスプライン補間を利用し,以下の関数fp2op_frame()で,リサンプリング(サンプリングレートの変換)を行う.ここででは,1kHzから360Hzへのダウンサンプリングとなる.
なお,通常,両足が地面と設置するので,フォースプレートは2台使用し,左右の脚でそれぞれ力学計算を行う必要がある.ここではのfp2op_frame()の引数fp_numとして1を選択すると左足の床反力が,2を選択すると右足の床反力を出力する.
また,フォースプレートの座標系はモーションキャプチャの座標系と異なる.次のfp2op_frame()は,同時にフォースプレート座標系から,モーションキャプチャの座標系に変換し,リサンプリング後にモーションキャプチャのデータ数に合わせる.なお,サンプルとして提供しているモーションキャプチャとフォースプレートのデータの計測では,トリガースタート同期を行い,データの開始の時時刻は同じである.
# リサンプリング(サンプリングレートの変換)のためにUnivariateSpline()を使用
# 重み係数s=0とすることで,平滑化を行わず,補間する.
def spline_interpoation(vec_data, sf_original=1000., sf_new=360.):
vec_copy = copy.copy(vec_data)
vec_data_t = vec_copy.T
len_num = len(vec_data)
len_vec = len(vec_data_t)
rate = sf_new / sf_original
time_old = np.arange(0, len_num) / sf_original
time_new = np.arange(0, len_num * rate)/(sf_original * rate)
w = [np.isnan(x) for x in vec_data_t]
spl = [0] * len_vec
for i in range(len_vec):
vec_data_t[i][w[i]] = 0.
w[i] = ~w[i]
spl[i] = UnivariateSpline(time_old, vec_data_t[i], w[i], s=0, k=3)(time_new)
return np.array(spl).T
# サンプリングレート 1kHzのforce plateのデータを
# motion caputreのサンプリングレート(360Hz)に合わせて変換
# UnivariateSpline()を使用.重み係数s=0とすることで,平滑化を行わず,補間する.
def fp_interpolation(file_path_fp, fp_num:int=1, fp_type:str='f', sf_original=1000., sf_new=360.):
fp_vec = extract_fp_vec(file_path_fp, fp_num, fp_type)
return spline_interpoation(fp_vec, sf_original, sf_new)
# リサンプリングと座標変換をまとめて行う
# モーションキャプチャのデータの長さが必要なため,モーションキャプチャのデータのファイルパスも必要となる
def fp2op_frame(file_path_fp, file_path_op, fp_num:int=1, fp_type:str='f', sf_original=1000., sf_new=360.):
op = extract_marker(file_path_op, 'RHand') # 右手データを使用(何でも良い)
len_op = len(op) # モーションキャプチャのデータの長さ
fp = fp_interpolation(file_path_fp, fp_num, fp_type, sf_original, sf_new)
return fp[0:len_op]フォースプレートについては
の記事も参照されたい.
データの取得例
モーションキャプチャのデータ:
以前と同様に
# CSVデータからヘッダだけ抽出
def extract_df_header(file_path):
return pd.read_csv(file_path, header=None, nrows=5, index_col=1).T
# skeletonの名前を抽出
def extract_skeleton_name(file_path):
df = extract_df_header(file_path)
marker_name = df['Name'][2]
position_col = marker_name.find(':')
return marker_name[:position_col]
# ファイル名とマーカの名前を引数に与えて各Linkの重心の加速度データを抽出する関数
def extract_marker(file_path, marker_name):
sk_name = extract_skeleton_name(file_path) # skeleton
df_main = pd.read_csv(file_path, header=[4]) # データだけ抽出
df = extract_df_header(file_path) # headerだけ抽出
df_selected = df[df['Name']== sk_name+':'+marker_name] # ヘッダがNameと一致する部分だけ抽出
selected_rows = df_selected.index # 一致する列
marker_data = np.array(df_main.iloc[:, selected_rows[-3:]].values) # 後ろから3個データを取得す
return marker_data[:, [2,0,1]] # OptiTrackの座標がYup(Y軸が上)のため,座標を入れ替えることで,Zupに変更するを使用して取り込む.
例えば,右手のリンクの原点(右手関節)の位置ベクトルは
extract_marker(file_path_op_6, 'RHand')のように取り込むことができ,以下のように確認できる.
r_hand = extract_marker(file_path_op_6, 'RHand')
plt.plot(np.arange(len(r_hand))/360., r_hand)
plt.xlabel('Time [s]')
plt.ylabel('Position [m]')
plt.legend(['x', 'y', 'z'])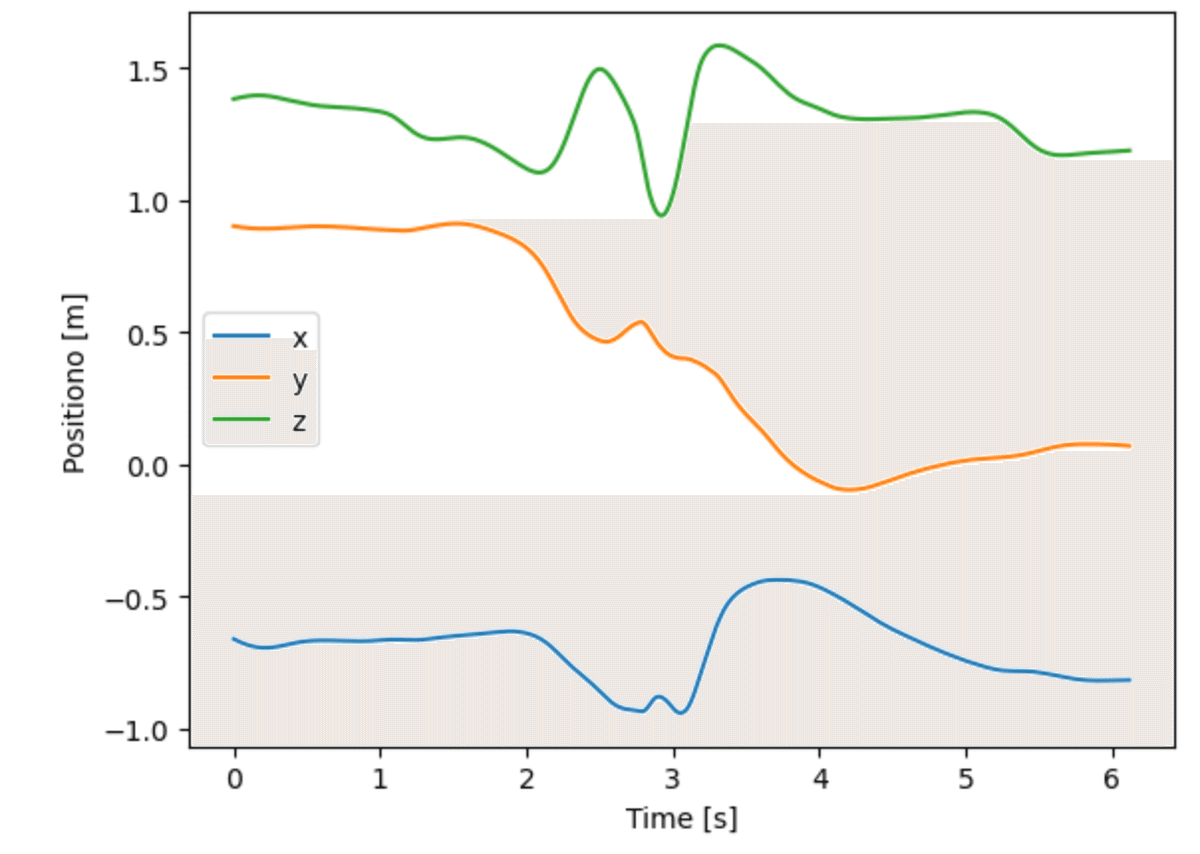
フォースプレートのデータ:
一方,右足に対応するフォースプレート2のデータは,先程述べたfp2op_frame()で座標変換とリサンプリングを行い,同様に確認できる.
fp_r = fp2op_frame(file_path_fp_6, file_path_op_6, 2, 'f')
plt.plot(np.arange(len(fp_r))/360., fp_r)
plt.xlabel('Time [s]')
plt.ylabel('Force [N]')
plt.legend(['x', 'y', 'z'])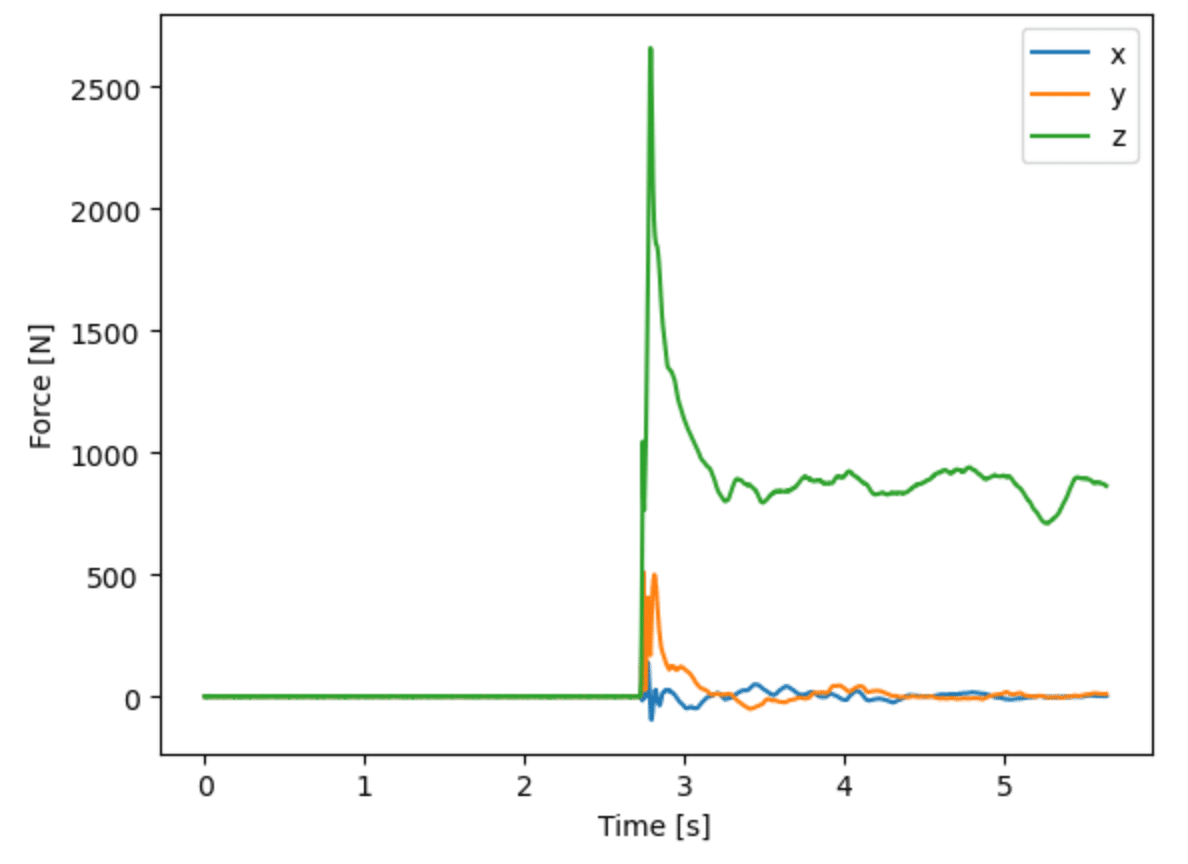
ニュートンの運動方程式による関節に作用する力の計算
モーションキャプチャとフォースプレートのデータから,身体各部に作用する力の計算を行う.第4章では,加速度データをサンプルデータとして提供したが,ここでは,モーションキャプチャの位置データから加速度を計算して,力学計算を行う.
class BodyLinkの定義:
使用するPythonのclassは基本的には同じだが,少し改変を行った.
ここでは,第4章で取り上げたclass BodyLinkに,
1.cg_ratio:重心位置ではなく,重心位置を計算するために必要な分配比(各部位の近位端と遠位端に対する内分比)
2.その計算のため必要な遠位端(後述)
のインスタンス変数を加えた.
1については,各部位の関節位置(近位端と遠位端)から,重心位置を計算するように変更している.そのため,末端の部位では2の遠位端の定義が必要となる.
また,前章のクラスをそのまま引き継ぎ,今回の計算に不要なインスタンス変数accを加筆しているので注意されたい.以下にclass BodyLinkを示す.機能的に改訂・加筆した部分に(new6)とコメントしている.
# new6:追記・変更箇所
class BodyLink:
def __init__(self, l_id:int, name, mass_ratio:float, cg_ratio:float):
self.l_id = l_id # linkのID
self.name = name # linkの名前
self.mass_ratio = mass_ratio # linkの質量分配比
self.cg_ratio = cg_ratio # linkの重心位置の分配比 (new6)
self.child_val = None # 子供の変数
self.sister_val = None # 兄弟姉妹の変数
self.distal_val = None # linkの遠位端の変数 (new6)
self.cg = None # linkの重心位置
self.acc = None # linkの重心の加速度
self.force = None # linkの関節に作用する力
# BodyLinkを一旦作成してから,その後に親子,兄弟姉妹関係をBodyLinkに与える.
def set_child_sister(self, child_val, sister_val):
self.child_val= child_val
self.sister_val = sister_val
# m * (acc - g)
def CgForce(self, bw):
gravity = [0., 0., -9.8] # 重力加速度ベクトル
return bw * self.mass_ratio * (self.acc - gravity)
# (new6)
# リンク(部位)の重心を計算するためには,リンクの原点(近位端)と遠位端の位置ベクトルが必要
# ただし,末端のリンク(部位)には子供のリンク(部位)がないので,リンクの遠位端(関節)の情報を得られない
# BodyLinkを一旦作成してから,その後に,各リンクの遠位端の位置をBodyLinkに与える.親子関係とは区別して利用
def set_distal_end(self, distal_val): # (new6)
self.distal_val= distal_val
# Inverse Dynamics Newton equation(改訂)
def ID_Newton(self, bw, sister=False, fp=True):
if self.name == 'RToe': # (new6)
return self.force
elif self.name == 'LToe': # (new6)
return self.force
elif self.l_id == 0:
return 0.0
elif sister == False: # 部分(そこから遠位:子供のみ)の解析
f = self.CgForce(bw)+\
self.child_val.ID_Newton(bw, sister)
self.force = f
return f
elif sister == True: # 全身解析(兄弟姉妹を含む)
f = self.CgForce(bw)+\
self.child_val.ID_Newton(bw, sister)+\
self.sister_val.ID_Newton(bw, sister)
self.force = f
return f
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
# 合成の質量(全質量)の計算
# sister == False なら,部分解析(そのリンクの遠位側だけ計算)
# sister == True なら,全身解析(兄弟を含める)
# bw: 体重
def Resultant_Mass(self, bw, sister=False):
if self.l_id == 0:
return 0.0
elif sister == False: # 部分(そこから遠位のみの)解析
return bw * self.mass_ratio + (self.child_val).Resultant_Mass(bw, sister)
elif sister == True: # 全身解析
return (bw * self.mass_ratio +(self.child_val).Resultant_Mass(bw, sister) +
(self.sister_val).Resultant_Mass(bw, sister))
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
# m * cg
def WeightedJoint(self, bw):
return bw * self.mass_ratio * self.cg
# 合成の(全)WeightedJoint
# Σ m_i * cg_i
# sister == False なら,部分解析(そのリンクの遠位側だけ計算)
# sister == True なら,全身解析(兄弟を含める)
def Resultant_WeightedJoint(self, bw, sister=False):
if self.l_id == 0:
return 0.0
elif sister == False: # 部分(そこから遠位のみの)解析
return self.WeightedJoint(bw)+\
(self.child_val).Resultant_WeightedJoint(bw, sister) #, sister)
elif sister == True: # 全身解析
return self.WeightedJoint(bw)+\
self.child_val.Resultant_WeightedJoint(bw, sister)+\
self.sister_val.Resultant_WeightedJoint(bw, sister)
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
# 合成重心
# Resultant_WeightedJoint() / Resultant_Mass()
# = Σ(m_i * cg_i) / Σ m_i
# sister == False なら,部分解析(そのリンクの遠位側だけ計算)
# sister == True なら,全身解析(兄弟を含める)
def Resultant_Cg(self, bw, sister=False):
return self.Resultant_WeightedJoint(bw, sister)/self.Resultant_Mass(bw, sister)
b_link = [0] * 21 # 配列の初期化
b_link[0] = BodyLink(0, '', .0, .0) # 0のときストップ
b_link[1] = BodyLink(1, 'Hip', .187, (1.-.609))
b_link[2] = BodyLink(2, 'Chest', .302, (1.-.428))
b_link[3] = BodyLink(3, 'Neck', .069, (1.-.821))
b_link[4] = BodyLink(4, 'RUArm', .027, .529)
b_link[5] = BodyLink(5, 'RFArm', .016, .415)
b_link[6] = BodyLink(6, 'RHand', .006, .891)
b_link[7] = BodyLink(7, 'LUArm', .027, .529)
b_link[8] = BodyLink(8, 'LFArm', .016, .415)
b_link[9] = BodyLink(9, 'LHand', .006, .891)
b_link[10] = BodyLink(10, 'RThigh', .110, .475)
b_link[11] = BodyLink(11, 'RShin', .051, .406)
b_link[12] = BodyLink(12, 'RFoot', .011, (1.-.595))
b_link[13] = BodyLink(13, 'LThigh', .110, .475)
b_link[14] = BodyLink(14, 'LShin', .051, .406)
b_link[15] = BodyLink(15, 'LFoot', .011, (1.-.595))
# 各リンクの遠位端も定義(遠位端の位置ベクトルを計算するためだけに必要な変数 (new6)
# 各リンクの遠位端も定義(遠位端の位置ベクトルを計算するためだけに必要な変数 (new6)
b_link[16] = BodyLink(16, 'Head', .0, .0) # 3 Neckの遠位端
b_link[17] = BodyLink(17, 'RFIN', .0, .0) # 6 RHandの遠位端
b_link[18] = BodyLink(18, 'LFIN', .0, .0) # 9 LHandの遠位端
b_link[19] = BodyLink(19, 'RToe', .0, .0) # 12 RFootの遠位端
b_link[20] = BodyLink(20, 'LToe', .0, .0) # 15 LFootの遠位端再帰的な力学計算では,末端のリンク(部位)のインスタンスchild_val には0を格納しておくことで,それ以上遠位の探索は行わない.しかし,末端のリンクの重心位置を計算するためには,遠位端の部分の位置ベクトルも必要となる.そこで,上記コードの最後のように,b_link[16]からb_link[20]のように,末端の頭部(Neckを原点とする),右手(RHand),左手(LHand),右足(RFoot),左足(LFoot)の遠位端を,Head, RFIN, LFIN, RToe, LToeとして定義した.
そして,set_distal_end()関数は,「各リンクの遠位端の位置ベクトル」をBodyLinkに格納する関数である.親子関係とは区別して利用し,後述する関数link_cg()によって重心位置を計算する際に,この関数で格納されたインスタンス変数distal_valを利用する.
親子関係,兄弟姉妹関係,遠位端の情報の格納:
以上のclassと関数を利用し,まず,
# 親子関係と兄弟姉妹関係を下記でb_linkのchild_val, sister_valに追記
child_sister_list = [
[1,2,0], [2,3,10], [3,0,4], [4,5,7], [5,6,0], [6,0,0], [7,8,0],
[8,9,0], [9,0,0], [10,11,13], [11,12,0], [12,0,0], [13,14,0],
[14,15,0], [15,0,0]]
[b_link[i[0]].set_child_sister(b_link[i[1]], b_link[i[2]]) for i in child_sister_list];
# 各リンクの遠位端の情報を格納.b_linkのcdistal_valに追記 (new6)
distal_end_list = [
[1,2], [2,3], [3,16], [4,5], [5,6], [6,17], [7,8],
[8,9], [9,18], [10,11], [11,12], [12,19], [13,14],
[14,15], [15,20]]
[b_link[i[0]].set_distal_end(b_link[i[1]]) for i in distal_end_list];によって,親子関係と兄弟姉妹関係と,遠位端の情報をchild_val, sister_val, distal_valに格納する.
床反力の格納:
さらに,左右の足のインスタンスforceには,以下のように,先に定義したp2op_frame()関数を利用して,フォースプレートの床反力データを,今回新たに加えた末端のリンクの遠位端(19:右足つま先RToe,20:左足つま先LToe)に格納する.
b_link[19].force = fp2op_frame(file_path_fp_6, file_path_op_6, 2, 'f')
b_link[20].force = fp2op_frame(file_path_fp_6, file_path_op_6, 1, 'f')ニュートンの運動方程式を解くID_Newton()は,つま先のリンクに対しては,床反力を取り込むように
def ID_Newton(self, bw, sister=False, fp=True):
if self.name == 'RToe':
return self.force
elif self.name == 'LToe':
return self.force
...
と定義されているので,ニュートンの運動方程式の再帰計算の最後に,これを床反力として取り込む.
各部位の重心の位置ベクトルの格納
モーションキャプチャのデータから位置ベクトルを抽出し,関節位置(遠位端を含む),重心位置を計算する関数を以下に定義した.
# (new6)
# リンクの近位端(リンクの原点の関節)と遠位端から重心を計算
def joint_vec(b_link, l_id, path):
if l_id == 0:
return .0
else:
joint_name = b_link[l_id].name
return extract_marker(path, joint_name)
def link_cg(b_link, l_id, path):
div_p = b_link[l_id].cg_ratio
body_q = joint_vec(b_link, l_id, path)
body_distal_q = joint_vec(b_link, b_link[l_id].distal_val.l_id, path)
return (1-div_p)*body_q + div_p * body_distal_qこれを利用し,以下のように各部位の重心の位置ベクトルを格納する.
# 各linkの重心を,self.cgに格納 ★
for n in range(1,16):
b_link[n].cg = link_cg(b_link, n, file_path_op_6)重心の加速度の格納
前章で述べた平滑化スプラインの関数を以下のように定義する.
# (new6)
# 微分と平滑化を同時にスプライン平滑化で行う
# order=0:変位(微分を行わない),order=1:速度, order=2:加速度
def smoothing_spline(vec_data, weight, sf, order=0, degree=4):
vec_copy = copy.copy(vec_data)
vec_data_t = vec_copy.T
len_num = len(vec_data)
len_vec = len(vec_data_t)
time = np.arange(0, len_num) / sf
w_a = [np.isnan(x) for x in vec_data_t]
spl = [0] * len_vec
for i in range(len_vec):
vec_data_t[i][w_a[i]] = 0.
w_a[i] = ~w_a[i]
spl[i] = UnivariateSpline(time, vec_data_t[i], w_a[i], s=weight, k=degree).derivative(n=order)(time)
return np.array(spl).Tここではこれを利用し,位置ベクトルから加速度ベクトルを計算するが,以下の関数
# (new6)
# 各linkの重心位置ベクトルから,重心の加速度ベクトルを計算
def set_acc(b_link, l_id, weight = .00001, sf = 360.):
b_link[l_id].acc = smoothing_spline(b_link[l_id].cg, weight, sf, order=2)
# それを,self.accに格納
def set_acc_link(b_link, l_id_list, weight = .00001, sf = 360.):
np.array([set_acc(b_link, n, weight, sf) for n in l_id_list])で,以下のように重心の加速度をインスタンス変数accに格納する.
# (new6)
# 各linkの重心の加速度ベクトルをself.accに格納 ★
set_acc_link(b_link, range(1,16), .00005, 360.)以上で,class BodyLinkのNoneで定義された空の各インスタンス変数(child_va, sister_val, distal_val, cg, acc, force)に,力学計算を行うために事前に必要なデータを格納することで,今回の力学計算の準備が整った.ただし,各部位(関節)に作用する力forceには,後に力学計算を行うメソッドID_Newton()によって力を計算し格納するのだが,遠位端のforceには別途事前に反力データを格納する必要がある.
逆動力学計算(ニュートンの運動方程式)の例
以下の計算は,基本的には第4章
と同じであるので,再帰計算による力学計算の詳細は,第4章を参照していただきたい.
台から跳ぶ降りて,片足(右足)で着地するタスクを行った例である.約2.5s以後にフォースプレートに着地した.
右腕だけの計算例:
まず,部位4(右上腕)の関節(右肩)に作用する力を計算(sister=Falseとすることで,その先のリンクだけ計算.兄弟姉妹は無視)する.
force_4 = b_link[4].ID_Newton(86.) # sister = False (default)このグラフを描くと
plt.plot(np.arange(len(force_4)) / 360., force_4)
plt.ylim(-55,130)
plt.xlabel('Time [s]')
plt.ylabel('Force [N]')
plt.legend(['x', 'y', 'z'])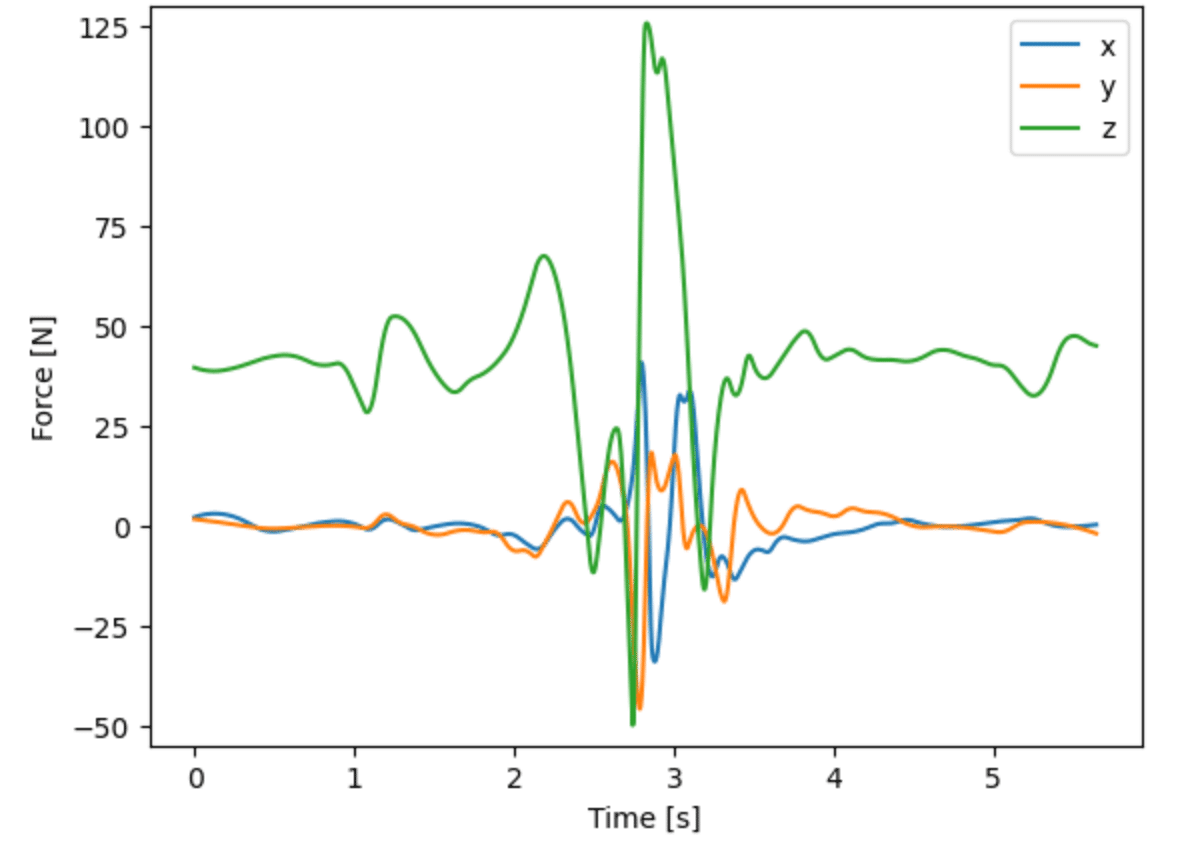
右手に作用する力も,上記の再帰の計算過程で計算されている.
plt.plot(b_link[6].force)
plt.plot(np.arange(len(b_link[6].force)) / 360., b_link[6].force)
plt.ylim(-55,130)
plt.xlabel('Time [s]')
plt.ylabel('Force [N]')
plt.legend(['x', 'y', 'z'])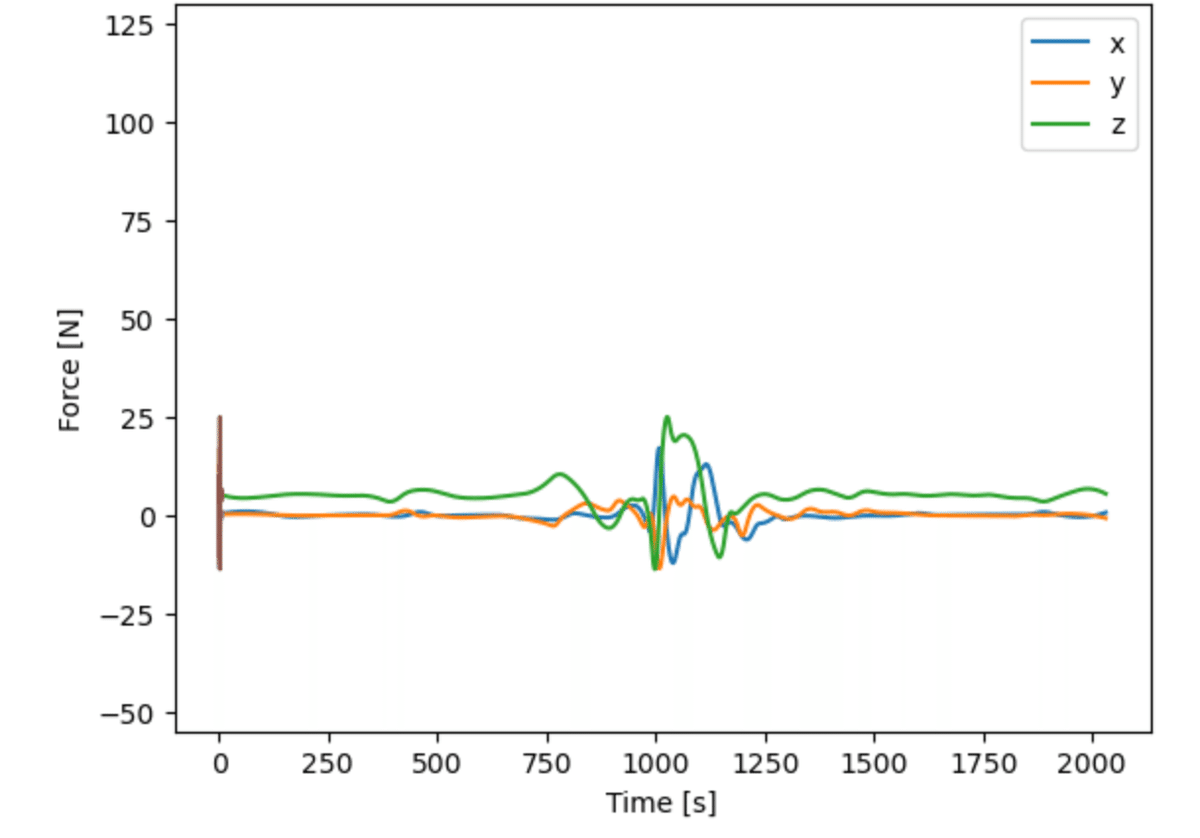
全身の計算例:
以下は,部位1に作用する力を計算(sisiter=Trueとして,全リンクの関節に作用する力を計算)することで,全身の逆動力学計算を行っている.これは身体重心に作用する力と等価である.
b_link[1].ID_Newton(86., True)cg_force = b_link[1].force
plt.plot(np.arange(len(fp_r)) / 360., cg_force)
plt.xlabel('Time [s]')
plt.ylabel('Force [N]')
plt.legend(['x', 'y', 'z'])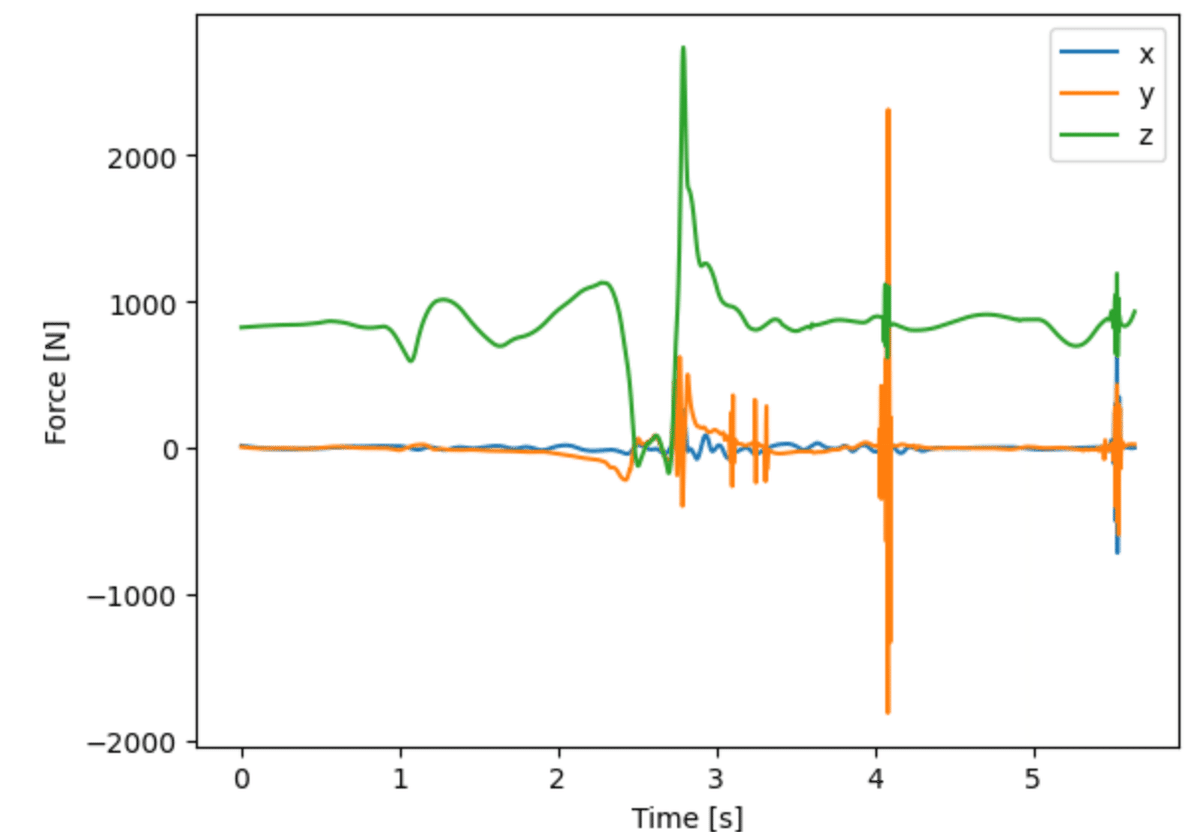
身体重心に作用する力を図6に示した.
台上(約2.5sより前)では力計測を行っていないため,推定値になる.着地後(約2.5 s以後)は,フォースプレートのデータを使用している.着地後は床反力とほぼ一致している.
まとめ
以下に,class BodyLinkと関連する関数の関係をまとめた.
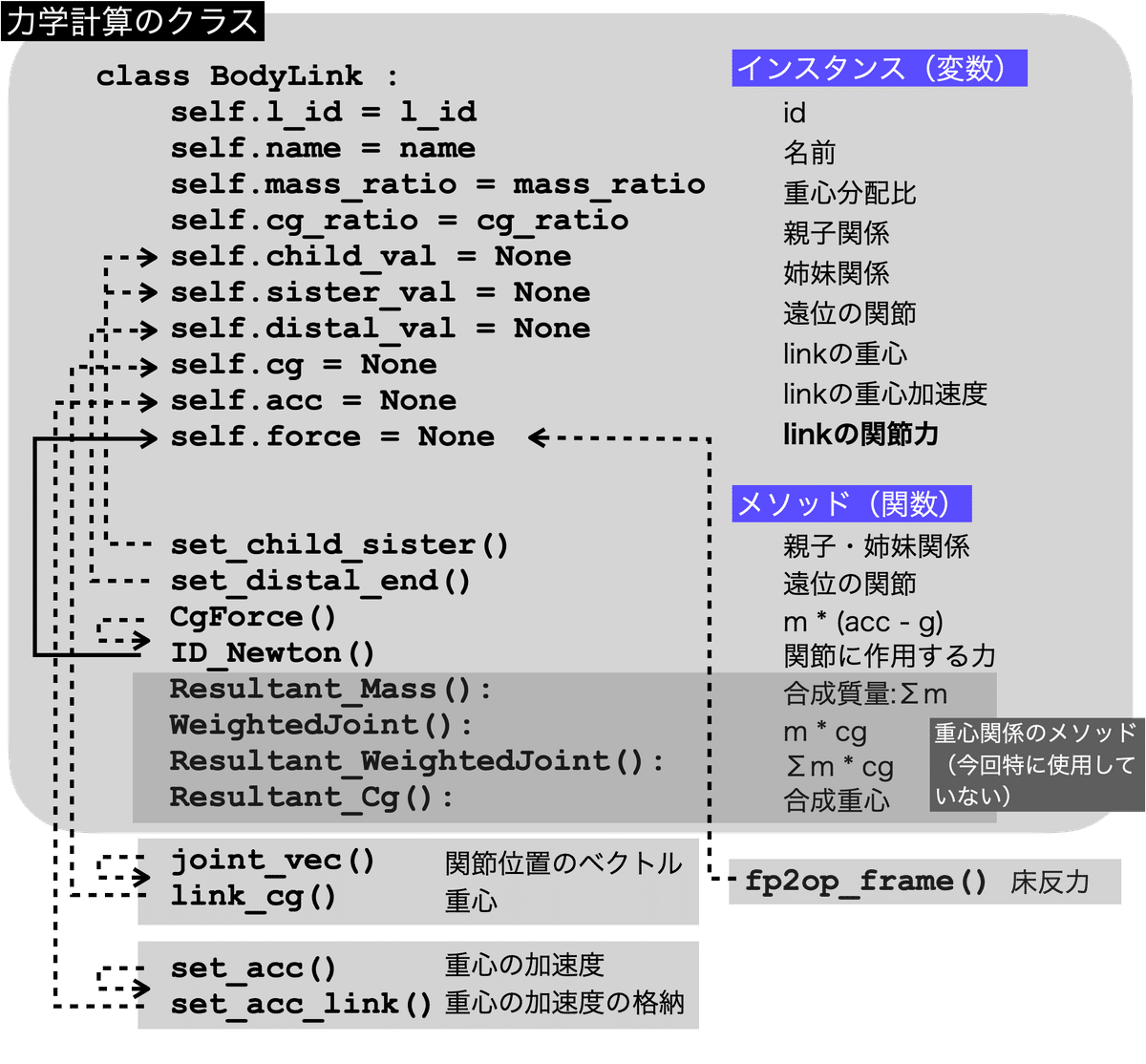
以上で,力学計算のうちニュートンの運動方程式により関節に作用する力の計算を示した.以後は,オイラーの運動方程式によって,関節に作用するトルクの計算を行う.
次章以降について
回転の力学(オイラーの運動方程式)の逆動力学解析によって関節に作用するトルクの計算の準備を行っていく予定である.並進の力学・運動学と異なり,回転の力学・運動学はやや複雑になるが,基本的には並進と同様である.それに付随して,スティックピクチャなどを描くツールもPythonで作っていきたい.


【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
