
Sports Biomechanics Geek #2 〜動力生成と伝達〜
バイオメカニクスでは関節に作用するトルクを計算することで,運動のメカニズムを探ろうとすることが多い.もし,アクチュエータ(モータ,筋肉など)が作用する関節を局所的に制御するだけなら,トルクの役割は明確だ.しかし,ヒトは負荷が大きくなるにつれ,一つの筋肉や一つの関節でその負荷に対処することができずに,離れた部位の筋肉へ力を分散・分担させる必要が出てくる.このようなときにトルクの物理的意味は全く異なり伝達や分散が役割となる.そしてヒトらしい運動はこの動力の伝達が特徴づけているだろう.また,単にトルクを計算するだけでは身体運動の物理的意味は見えてこない.筋力は動力を生成しながら同時に伝達を担うが,トルクはこの伝達の記述に向いていない.動力の伝達を観察するなら力学的エネルギーの時間変化を計算するのが良い.
はじめに
言うまでもなく身体運動に限らず物体の運動を拘束するルールが運動方程式であり,身体の各部位間の力学的エネルギーの変化や流れの計算にも運動方程式は必要となる.運動方程式が力学計算の核である.また,運動方程式を積分(シミュレート)すれば,運動(速度や位置)を予測・再現でき,トルクを入力とすることで身体運動を計算できる.したがって,運動方程式を扱うことで運動の特徴や観察される多くの関係を記述できる.
身体を動かすアクチュエータは筋肉で,それは関節の駆動力(トルク)を生成するので,例えば速く投げるコツなどを,トルクや筋力に還元したくなるのは自然な発想だろう.では,身体運動におけるヒトらしい運動のメカニズムを考える上で,関節に作用するトルクを計算したり,運動方程式だけで議論を行えば,メカニズムが見えてくるだろうか?運動方程式だけで議論は閉じるだろうか?

たとえば,図1のように空中の後脚(蹴り脚側)の膝に作用する力$${\bm{f}_2}$$を考える.この膝に作用する力を解析する際には,足(部位$${1}$$)と下腿(部位$${2}$$)の運動方程式を計測できれば膝関節に作用する力を
$$
\bm{f}_2 = m_1 (\ddot{\bm{x}}_1 - \bm{g}) + m_2 (\ddot{\bm{x}}_2 - \bm{g})
$$
算出できることに気がつくだろう.ここで,$${m_i, \bm{x}_i}$$を各部位$${i}$$の質量,重心位置,$${\bm{g}}$$を重力加速度とする.
これはマガジン「動かして学ぶバイオメカニクス」
でも述べてきたが,関節に作用する力やトルクはそこから遠位側の全部位の運動方程式を加算するだけで算出できることに由来する.
ここで注意したいことは,膝関節に作用する力$${\bm{f}_2}$$は,身体の残りの部位($${i = 3, \cdots, n}$$)を加算しても算出することができ,
$$
\bm{f}_2 = -\left( m_3 (\ddot{\bm{x}}_1 - \bm{g}) + \cdots + m_n (\ddot{\bm{x}}_n - \bm{g}) \right)
$$
のようにも解くことができるということである.つまり,関節に作用する力は,実際にはその関節をまたぐ両サイドの部位のおしくらまんじゅうの相互作用で定まることを示している.理論上は,片方から解くことができるため,力が順次伝達すると誤解する人がいるかも知れないが,反対側から押す力が弱ければ,そこに強い力は作用しないように,質量などによる重み付けはあるが,各力は相互作用がある全身の加速度の振る舞いによって決まる.各部位のひとつひとつの運動方程式は,そのローカルな(局所的な)釣り合い(ダランベールの原理の意味で)関係を定めているだけで,それは多体系では「身体全体の運動が定まって初めて,ローカルな力が定まる」.
普段の経験から「いやいや,少し手を動かすだけなのに脚の動きなど関係ないでしょう」と感じる人は多いはずである.それは,他の部位が手と比較して重く,地面に拘束されているため,脚は動いていないこととほぼ等しい状態になるためである.厳密には,もし部位が固定されていないなら,たとえ指先を動かすだけでも,同様に全身の運動で定まる力である.
たとえば,膝では,膝に作用する力$${\bm{f}_2}$$は,足部と下腿の
$$
\sum_{i=1}^{2}m_i (\ddot{\bm{x}}_i - \bm{g})
$$
と,残りの部位の
$$
-\sum_{i=3}^{n}m_i (\ddot{\bm{x}}_i - \bm{g})
$$
の両方から「相互作用」の力であるので,値を計算はできるが,この式からは起源をたどることはできない.全ての部位が,すべての部位と相互作用している.作用を示す矢印は永遠に続く無限ループとなる.ある部位の運動を特定の部位のトルクに還元することはできないだろう.つまり力の貢献度は運動方程式だけからは計算できないはずだ(補足1).
これに対して,力学的エネルギーの時間変化(パワー)は,「動かして学ぶバイオメカニクス #16 〜動力の伝達〜」
で説明したように,関節を経由する力学的エネルギーの流れや伝達を定めることができる.
力は身体各部位の相互作用(加速度)の差分的な情報で流れや伝達という概念はないが,エネルギーの変化は流れを定める情報と考えるとよい.まずは力とエネルギーに関して,このような特徴をよく理解すべきだろう.
運動方程式自体が力の伝達を記述するには不向きだとしても,力学的エネルギーの時間変化の計算において運動方程式は欠かせなく,動力伝達の問題を考える上で,身体運動における運動方程式の意味について考えていく.
運動方程式
多様な運動方程式
剛体の運動を記述する運動方程式は実はいろいろな方法で表現することができる.たとえば,運動を並進と回転に分けて,並進の運動はニュートンの運動方程式で記述し,回転の運動はオイラーの運動方程式で記述するニュートン・オイラーの方法がある.ロボティクスでは,これは単に力学計算のツールに過ぎないかもしれないが(少なくとも教科書にその物理的意味は書かれていない),身体運動では単に並進と回転のダイナミクスを記述するという以上の意味を持ち,力や動力の伝達と密接に関係することはすでに述べた.
運動方程式を記述する方法は,これ以外にも,最小の状態で運動を記述するラグランジュの運動方程式(Lagrange equation of motion)や,耳慣れないかもしれないが,拘束条件を含む場合ケイン型運動方程式(Kane's equation of motion),ジョルダンの原理(Jordan's Principle)を利用する方法など様々ある.運動を支配するルールはある意味ひとつしかない.しかし,その同じルールを表現する方法は複数存在する.
力学でよく知られたラグランジュの運動方程式は一般化座標(generalized coordinate)と呼ばれる,最小の自由度の変数で運動を記述する.これに対して,ニュートン・オイラー法は内力(internal force)と呼ばれる,運動を記述する目的にとっては無駄な力が式に現れる.内力や余計な変数は式を冗長にしてしまうが,運動方程式自体の長さはむしろ短くなる.たとえば身体が15個の部位で構成されるとして,15個の部位のラグランジュの運動方程式は長すぎて書き下すことはもはや困難であるが,ニュートン・オイラー法なら手で紙に計算して書き下すことも十分可能だ.
身体運動の力学解析における内力としては,関節に作用する作用・反作用の力が代表的で,バイオメカニクスでは関節力や関節間力などと呼ばれることがある.これは作用・反作用の力なのでシステム全体の系(system)では相殺され,「系から見る」とこれは仕事をしない無駄な力だが,身体運動ではエネルギーを伝達するという特別な意味を持つ.系内部での移動は,系全体の変化に影響しないことは容易に造像ができると思う.
したがって,身体で動かす動力を身体全体で作り出し,冒頭で述べたように,身体の末端の手首や足首のトルクは下肢や体幹が発揮するトルクと比べるとかなり弱く,スポーツでは特にだが,手などが発揮するトルク単独で道具などを操作することは難しく,動力を身体に伝達・分配するということを行う必要がある.したがって,身体運動の解析にとっては,内力が陽に見える形式の運動方程式のほうが便利な側面が多い.
身体運動における並進と回転のダイナミクスの役割
前章
の力学問題を考える際には,並進と回転のダイナミクスに分解して考えるとわかりやすい(補足1).
平たく述べると,身体の動かし方には,「押したり」(引っ張ることもあるが,基本は押す),「回す」2種類があると考えてよいだろう.それらは,並進のダイナミクス,すなわちニュートンの運動方程式と,回転のダイナミクス,すなわちオイラーの運動方程式に対応する.これらは関連して運動に寄与し,身体運動においても並進と回転のダイナミクスに機能分担がある.
身体運動では動力の伝達において,これらが密接に関係する.
動力の最終的な出口はトルクではなく力である
身体運動は,最終的に床反力や道具に作用する外力として,環境(身体と道具など)との相互作用の力として発揮されることが多いが,末端の部位の関節で発揮するトルクは決して強くない.末端の部位で大きな並進の力が作用した際に全身や他の部位で支えることはできるが,末端の部位に作用する大きなトルクを他の部位で支えることはできない.また,末端部位の関節速度が大きくなると,粘性抵抗によってさらに筋肉内部でエネルギーを消散し,外部に発揮するトルクがさらに小さくなってしまう.
しかし,末端の部位の関節に作用するトルクが弱くても,大きな回転力(トルク)を環境側(道具など)に作用させることは可能だ.たとえば,バッティングやゴルフスイングでは,バットやクラブに大きなトルクを与えて高速に回転させているが,実はバットやクラブを回転させているトルクは,右手と左手が与える並進の力が,反対方向に作用することで発生する偶力(force couple)である.偶力はトルクとして物体に作用する.
偶力については
を参照されたい.図2のように,2つの力が作用する点が離れ,このクラブの場合だと,おおよそクラブに対して垂直な方向の成分が偶力としてクラブの回転力を発生する.
ちなみに,補足2でも説明するが,クラブに作用する偶力は加算すると,力としては相殺される力である.

図2のような偶力を与えるためには両手で閉ループ(閉リンク)を構成する必要があるが,偶力に頼らず片手でも環境側に回転力を与えることができる.たとえばラケットの高速スイング中にラケットに与える力のモーメントのほとんどは,手が与える並進力由来の力のモーメントである.図3にように回転方向に対して反対方向の力をグリップで与えることで,ラケットには回転力を与えられる.手首の関節が与えるトルクは,後ろに戻らないようにストップするときには寄与するが,前方に回転する際にはほとんど寄与しないことが予想される.

このように,両手で道具を操作する場合,偶力と図3のような接線方向の力の二つの力で道具を回転させることができる.偶力は左右の力の差分(左右の力のうち打ち消し合う成分)のうち道具を回転させる成分である.一方,左右の力の和が合力となり,この合力のうち接線方向成分も道具を回転させる.偶力と合力(外力)の関係については補足2を参照されたい.
このように,抹消・末端の部位が道具などの環境と相互作用する際,その部位の関節に作用するトルクではなく,主として並進の力が環境に影響を及ぼしていることをよく考えておく必要がある.
末端の力学について述べたが,ここでもう一つ強調しておきたいことは,運動を最も強く拘束するのは,手先や足先などの出口の部分だ.たとえばランニングは地面と身体間に作用する床反力(地面反力)が身体に作用することで,走速度を規定する.特に走速度を最終的に定めるのは鉛直方向の力ではなく水平の床反力である.
バイオメカニクスの研究では,たとえばラケットの速度と何かの関係を論じたくなる.しかし,よく考えてみてほしい,まずはこのような動力の出口であるラケットの力学や運動学を明確にすることが大切だ.それを満たさなくては,ラケットを回転できないのだから.
以上から,身体運動の運動パターン形成の力学は末端の力学に拘束され,たとえスイング動作のような回転が中心の運動でも,特に回転の運動方程式よりも,特に並進の運動方程式を中心に拘束されていることがわかる.
押す力学
並進の力は物体を押したり引っ張る力として機能する(ここでは,押す力を主として考えていく).当たり前だが,その大きな力発揮のためには筋肉にとって押す対象が必要となる.「暖簾に腕押し」という諺があるが,軽いなど動きやすい対象に対しては,大きな力発揮を行うことができない.たとえ大きなアクチュエータ(筋肉)であっても,いつでも好きなだけ力発揮ができるわけではなく,押し返してくる対象や力が必要となる.
相対的に小さい力発揮で事足りる場合には,わざわざ何かを押さなくても,手先や足先で十分な相互作用ですむこともあるが,投げるボールの質量が大きくなったり,投擲距離を競う場合には,身体が地面などを押すことでより大きな筋肉の力を得ることができる.
例えばバーベルを挙上する運動では,身体は地面とバーベル間で身体各部位間でおしくらまんじゅうを行っている.一方,綱引きにおける身体の状態を想像していただきたい.この運動ではなにか腕で引っ張る運動ということを想起しがちだが,やはり地面と肩の間でのおしくらまんじゅうが中心に行われている.腕の力は下肢や体幹の力と比してかなり脆弱なので,受動的に引っ張られているだけだろう.ところが,肩から地面にかけては,まさに身体のおしくらまんじゅうの運動が行われている.ゴルフスイングなら手と地面間でおしくらまんじゅうがおこなれている.
押すためには対象が必要で,押される必要があるということは,筋レベルで大きな力を発揮するためには,筋肉に張力が作用している必要があるということを意味する.これは運動連鎖の概念とも関係すると思われるが,またの機会に述べることとする.
動力源と伝達部位は離れている
これまで述べてきたように,「押すことによって初めて筋肉はより高い力発揮が可能となる」ということに注意したい(ただし,筋肉がもつ弾性はあまり関係がない).
このとき,もう一つ注意したいことは,地面を押している部位と,押されたい場所は「離れている」ということである.ランニングなら身体重心を押したいし,ゴルフスイングならゴルフクラブを押したい.そこには身体の多関節(多体系)を介した相互作用による伝達が必要となる.身体にとって相対的に大きな出力を伴う運動では,動力源とその出力先が離れているがゆえに,伝達が必要となる.またその動力源は一つではなく,分散している.したがって,動力生成を能力に応じて分担することも重要だ.
ゴルフスイングでは左右の両手で作り出す偶力で大きなトルクをクラブのグリップ部に作用させることができると述べたが,それでも,その偶力(にようるトルク)では十分クラブを加速するにはエネルギーが足りないため,身体の他の部位からの動力の供給が必要となる.
さて,ここで一つの関節だけを考える.そこには二関節筋も含めて複数の筋群が関与する.このとき関節に作用するトルクは,おおよそ筋肉の横断面積の3乗程度に比例して分配されることが知られている.関節レベルでは少なくとも,強い筋肉に分配される.複数の関節をまたぐ際にも,基本的には強い筋肉に分配するのが基本的な戦略として考えられる.
そして,隣の関節でまかなうことができない場合は,さらに隣へと負担が分配されることになる.
また,押すことの連鎖(おしくらまんじゅう)が必要で,弱い関節があると,伝達が難しくなる.これを,ここでは漏れ(leakage)と呼ぶこととする.太字で記述したが,これは力学などにおける学術用語ではない.しかし,相互作用のある多体系の運動を考えていく上で,重要な概念である.構造力学の設計で,弱い部分に応力が集中しそこで破壊が生じることと似ている.体幹は多くの筋肉があるため漏れを防ぐために迂回路を形成しやすいが,それが障害という歪みをもたらす事がある.また,ある部位を障害でいためたあと,それを補償するように動かして別の場所に障害を起こすことが知られている.
トレーニングではこのような漏れを減らすことが一つの課題となる.
押す力学を支える回す力学
前述のように,多くの場合,動力の最終伝達先は身体の末端で,それはトルクではなく並進の力で与えられる.そして出口でどのような出力が必要とされるか,出口の力学を明確にすることが先決だ.ゴルフスイングならクラブをどのように加速しているのか,投球の場合なら,どのようにボールを加速し,回転させ,リリース方向を制御するのかを理解せずに,身体の力学を考えてもあまり意味はないだろう.その理解の上で全身の問題を考えるべきだろう.
そしてその次に考える問題として,離れた部位から末端への大きな力への伝達である.たとえばゴルフスイングでは地面からクラブへ伝達する必要があり,下肢や体幹のような大きな動力源となる部位間のおしくらまんじゅうによって,動力が生成される.このとき,全身でおしくらまんじゅうを行い動力を発生しながら,クラブへの伝達も行う必要もある.
この伝達と押す力学を支えるのが回転の力学だ.ここで注意しておきたいことは,伝達したいのはトルクではなく,あくまでも並進の力である.そして,関節に作用するトルクは動力生成にも寄与するが,同時に伝達にも寄与することである.
たとえば,ゴルフスイングのような運動では,身体の各部位が回転している.腰も肩も腕も.しかし,おそらくこれらは,回転運動の連鎖が発生していると考えるのではなく,グリップ部に偶力を発生させるために,クラブと地面間のおしくらまんじゅうの結果発生する運動である.腰が回ってるのは,腰や肩などの解剖学的な拘束から,エネルギー伝達を行った後に,そのような方向にしか運動の自由度が残されていなかったためと考えるほうが妥当だろう.また,伝達を行うとき,関節の速度が大きいほどエネルギーを損失する.むしろ関節は動かないほうが効率が良い.
また,手首の関節のトルクが弱いのは簡単に実感できるだろう.質量も慣性モーメントも大きいクラブを腕を固定して,手首で回すことは困難である.手首で発揮できるトルクに制限がある以上,左右の手首の関節に作用するトルクを大きくする戦略を考えることは無意味である.クラブを回しているのは,あくまでも左右の手の並進の力で,それが偶力(トルク)や向心力や接線方向の力を生み出し,それら(全て)がクラブの回転を担う.クラブに伝達したいのはトルクではなく力である.
したがって少なくともゴルフスイングでは,回転のダイナミクスではなく,並進のダイナミクスを中心に考えるべきで,その力の伝達を支えるが各関節のトルクの役割で,たとえば腰を回すこと自体に,さほど意味はないだろう.腰は回っているが伝達の役割を終えた腰が,解剖学的な自由度の制約から,腰が自然に回転しているだけで,回転するしか自由度が残されていないと考えるほうが自然だろう.

腰を回すために動かしているのではなく,伝達のために股関節をあまり動かさないように力発揮し,伝達を終えた後にその勢いが運動として現れ,解剖学的な拘束から腰を回すしかないと考えるのが良いだろう.
したがって,運動連鎖を回転運動の連鎖として考えるのはどちらかというと誤りで,これは投球やバッティングでも同じだろう.
また,振動を考えればわかるが,積分によって力のピークから遅れて速度ピークが現れ,さらに位置のピークは遅れる.我々が運動として視覚で見ているの現象は,伝達のための力発揮の残像のようなものだ.
ただし,手と異なり肩や腰のトルクは手首と比較して大きいため,他の部位からのエネルギー供給なしでも十分動力として機能する.したがって投球では肩のトルクによって腕を回すことに貢献し,キック動作では股関節が下肢を回転させることに寄与することもでき,投球やキック動作などでは,トルクと並進に力による回転の両方を協調させて動かすことが求められる.
筋肉を使用しない伝達
多リンク構造で押す力学を支えるのが回転の力学であることは述べた.それをさらに支えるのがトルクであり筋力である.しかし,筋肉を使うこと自体負担が大きいので,筋肉を使用しないで伝達を担うことができるならそれが望ましい.実はそれは一部の関節の可動域の制約を利用することで実現できる.たとえば上腕を挙上している姿勢では肩関節は後方には動かない.また,肘・膝関節は蝶番関節のように自由度が拘束されている場合,内外反方向に対しては関節は固定されている.このような可動域や自由度の拘束を利用し関節を剛体化することで伝達を行うことがある.このような解剖学的な拘束条件を利用する伝達は筋力を使用しないため,効率の良い運動となる.
これは身体の構造を利用した負担の低減である.
ここで,一つ付け加えておきたいことがある.近位側や地面に近い部位で大きなトルクや動力を発揮したり,その動力を,力やエネルギーとして遠位側に伝達するためには,関節をむしろ動かさないことが重要となる.速く動くことはエネルギーの消費に繋がってしまう.たとえばスイング運動などのように,高速に動いている部位はすでにエネルギーを受け取っているため動いているのであって,伝達するときには速度が相対的に小さくすることが重要となる.
速度と時間のトレードオフ
このように相対的に大きな外力発揮には,地面を押すことが必要となる.一方で,地面を押すということは,伝達を必要とし時間との戦いが発生する.
残念ながら,筋肉がトルクを生成し伝達を担う上で,伝達に時間遅れが発生する.運動連鎖と呼ばれる現象だが,地面反力を瞬間的に手まで伝えることができない.
野球でも投球のように時間に余裕がある場合や,外野からの送球のように時間よりも速度が優先される場合は,地面との相互作用を積極的に利用するが,内野の送球で投球動作に要する時間や空間を大きく使うことが許されない場合は,ジャンピングスローを選択することもある.このように動力源から手先への伝達のためには,時間を必要とする弱点がある.力(速度)と時間のせめぎあいから,運動によって戦略は大きく変わってくるだろう.
また,伝達による助力を必要としない場合,制御はローカルに行うことができ,その分正確性がますメリットもある.たとえば,内野手は送球に時間の余裕があってたとしても,肩関節が発揮するトルクによって送球が十分にできる余裕があるなら,あえて伝達を制限するような動きを行うこともある.おそらくこれは正確性を優先して,あえて肩の並進運動に制約を与えていると考えているが,どこかで検証してみたい.
速度と拘束のトレードオフ
また一方で,地面を押すということは,地面と足間の位置関係を束縛し身体の自由度を大きく奪う.このような動作はとくに時間が制約される中で自由に身体を動かしたい場合には,空間的な自由度を奪うデメリットも発生する.そこで,身体能力の発達によって相対的に道具の負荷を小さくすることで,地面からの呪縛を解こうとする傾向にある.
バドミントンでは地面と接触している方が大きな力を得ることができるので,非力な選手はジャンプを行わず,地面を蹴りながらスマッシュなどの強打を行うことが多い.ところが,男子や身体能力の高い選手は,地面に足が拘束されていは自由に打つことができないため,シャトルコックに向かってジャンプして打つことを選択する機会が多い.テニスでも軽くジャンプしながらストロークするエア・◯◯と呼ばれる打法は,同じような意味を持つのだろう.
Speed-accuracy tradeoffという用語があるが,速度は正確性だけでなく,時間や運動の自由度も奪う性質がある.
おわりに
冒頭でも述べたが,関節に作用するトルク(筋力)でその関節をローカルで動かすことで,身体運動を形成するイメージを持っているではないだろうか.筋力由来の関節に作用するトルクが,動力源になっていることは自明であるが,そのトルクが直接作用する関節(だけ)を動かしてるというイメージは,多くの場合,むしろ当てはまらないことが多い.
たとえば投球であるなら,肩関節に作用するトルクは腕の回転に寄与するが,図3のラケットを腕に置き換えて考えれば,腕の回転は肩関節に作用する並進の力によっても加速されている.その力は全身の相互作用によって生成され,別の部位に作用する力を支えるのも別の部位の関節に作用するトルクである.腰が回転している理由は,腰を回転させたいがために回しているのではなく,肩や腕へ送り込む動力を生成し伝達した「後」に,解剖学的な幾何学拘束から回るしかなかったと考えるほうが妥当だろう.
このような伝達を支える部位では運動を止めることはできないが,むしろできるだけ動かないほうがよいはずだ.厳密に述べると,トルクと比較して回転の慣性力が小さい方が良い.
動力の伝達の記述に適している物理量は,力学的エネルギーの時間微分である.これは筋肉による関節を介したエネルギーの流入・流出,また内力(関節間に作用する作用反作用力)を介したエネルギーの伝達を表すことができることは,これまでマガジン「動かして学ぶバイオメカニクス」
で示してきた.このように力学的エネルギーの時間変化は,エネルギーの流れなどを可視化・数値化することには向いているが,メカニズムを考える上では,やはり運動方程式は必要である.
最初の問いに対する答えを明確には示していないが,身体運動のメカニズムを考えていく上で,運動方程式だけで議論を閉じても,エネルギーベースの議論だけで閉じても,答えは見えてこないだろう.また,貢献度のような数値だけを議論しても何もわからない.トルクでも力学的エネルギーでも同じだが,何かが大きい小さいといった数値や関係性だけではなく,身体運動におけるそれぞれの物理的意味を考えることが求めれる,特にスポーツでは,何かを大きくすると,何かが小さくなるというトレードオフや弁証法的な構造の中で考える必要があり,短絡的な考えに陥らないことが大切だ.
補足
補足1:貢献度
運動方程式だけで運動の貢献度を記述することはおそらくできないだろう.理由は簡単だ,運動方程式は隣の部位との相互作用は記述するが,前述のようにどの部位もダイナミクスは全身で決まり,運動方程式が記述する関係は無限ループとなり,そもそも起源をたどることはできない.運動方程式は伝達の記述には向いていない.
そもそも,色々なレベルの貢献度があるが,関節のトルクに帰着させる貢献度自体にあまり意味がないように思える.少なくともここで取り上げたように,動力生成,伝達などの役割がある.仮にそれらをひとつの貢献度で数値化し示すことができたとしても,身体各部で起こっていることの物理的意味をよく考えることが大切だ.
補足2:クラブやバットに作用する偶力と合力
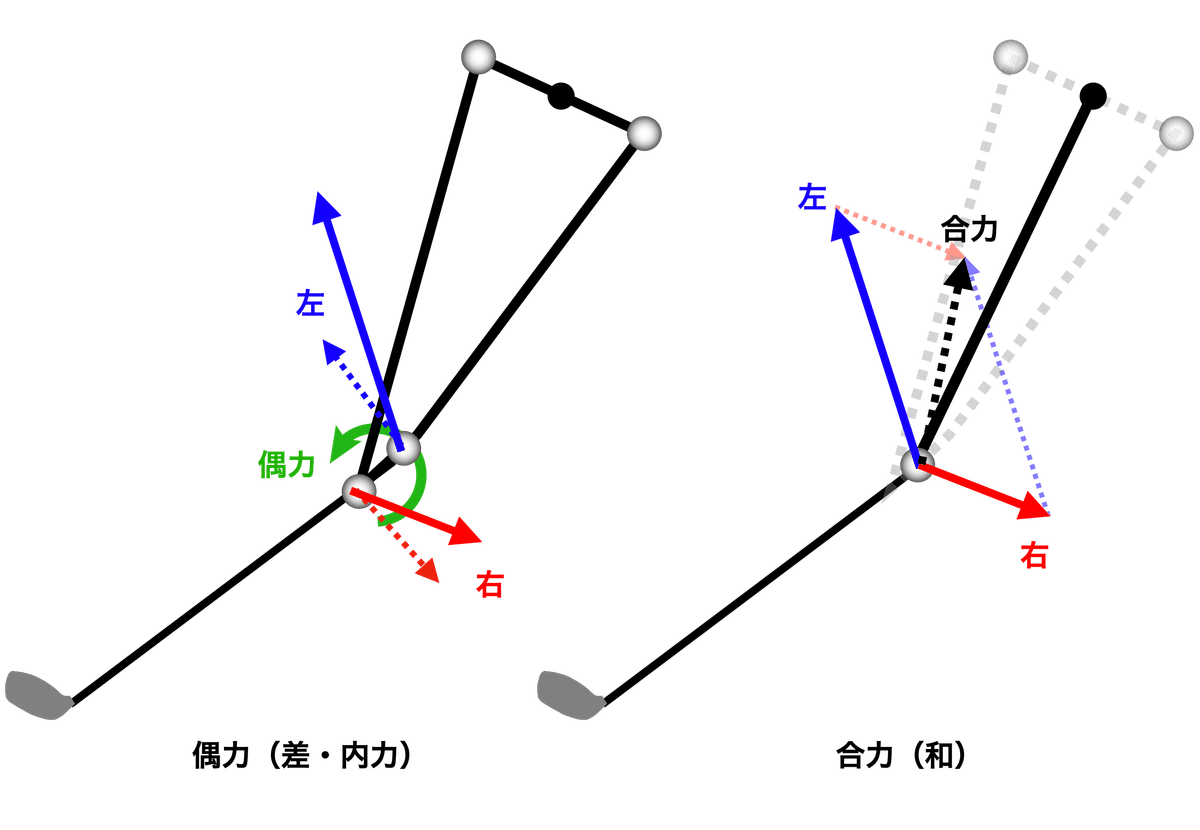
図5に示すように,ゴルフクラブには,右手と左手の力が作用する.それらの力の作用点の位置は一般に離れている(図5左).これはバットでも同じだ.このためクラブには一般に偶力が作用する.偶力については
を参照されたい.偶力は反対向きで同じ大きさの力の組み合わせだが,同じ場所に作用してはトルクを発生しない.これらの力は,異なる直線上に並び,異なる場所に作用する必要がある.
図5左のように力の作用点が,クラブのシャフト軸の直線上の異なる位置に存在すると考えれば(厳密にはシャフトは太さがある),その軸に垂直な方向に作用する2力がクラブの回転を生み出す偶力となる.左右の力のうち,回転を引き起こさない成分を含めれば,偶力の組み合わせの候補は無限にあるが,クラブに回転を引き起こす候補は図5左の破線のようになる.これは左右の力の「差分」のうちシャフト軸に対して垂直な成分を取り出している.このように二つの力ベクトルの「差分」に相当し,相殺される力は内力(internal force)と呼ばれるが,内力のうち,力の作用点が異なることで回転を引き起こす力のペアを偶力と呼び,さらに偶力のうちクラブに回転を引き起こすのシャフト軸に垂直な成分だけ,ピックアップしたのが図5左の偶力である.
一方,偶力が「差分」であるのに対して,左右の二つの力ベクトルの「和」が合力で(図5右,黒色破線),これがクラブの並進の力として作用する.この合力のうち,クラブのシャフト軸方向に垂直な成分が,図3の力に相当し,やはりクラブの回転力を生み出す(図6).

ここで整理をしておくと,道具(クラブやバット)に,右手と左手から,それぞれ力とトルクに作用すると考える.つまり二つの力と二つのトルクが,道具に作用すると考える.しかし,ゴルフスイングやバットスイングでは,右手と左手が与える各トルクは非常に小さいことが予想される.ここでは右手と左手が直接クラブに与えるトルクは微小として,議論の対象外とする.
すると,道具を回転させる力は,並進の力だけで与えることになるが,左右の二つの並進力の作用点が異なれば,左右の総和として
偶力(すなわちトルク,左右の力の差分のうちシャフト軸に垂直な成分のペア)
合力(左右の和)
が発生し,1が偶力として回転力を,2も図3で示したように接線方向の成分が回転力を生成することになる(図6).手首のトルクが弱くても道具を回転させる力を,左右の並進の力で,1と2の二種類の回転力として与えていることに注意をされたい.
したがって,バットやクラブの挙動を深く知るには,左右の力を分離して計測する必要がある(文献1).
なお,クラブの運動計測から計算される,逆動力学計算によってクラブに作用するトルクとして計算されたもののほとんどが,先程述べた1の偶力に相当することに注意をされたい.また,その偶力も,スイング前半で発揮されるだけだ(文献2).
関節に作用するトルクが弱くても,左右の手に作用する並進の力で道具に十分なトルクを与えることができる.というよりも,身体運動では,末端の部位が作用するトルクは小さいので,むしろ並進の力で環境と相互作用している.ただし,ローカルでエネルギーを供給できず,伝達が伴うため,そのようなエネルギー供給には時間がかかることにも留意をしておく必要があるだろう.
参考文献
1)太田,持田.ゴルフクラブに作用する左右6分力の.高精度計測,日本機械学会シンポジウム:スポーツ工学・ヒューマンダイナミクス2018講演論文集,B-11,2018
2)太田,仰木,澁谷.ゴルフスイングにおける内力を利用したエネルギー伝達,日本機械学会シンポジウム,スポーツアンドヒューマンダイナミクス2012講演論文集,p.293-298, 2012



【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
【データの計測について】
スポーツセンシング社のスタジオで,フォースプレートやモーションキャプチャを利用した計測も行えます.出力されるデータと,ここで示したプログラム(入力データの取り込み関数を少々改変する必要があるが)で,同様な解析を行えますので,まずはお気軽にお問い合わせください.
