
モーションにおける3次元回転 #3 〜複素数による2次元平面の回転〜
複雑な3次元の回転について説明する前に,複素数を利用した平面内の回転運動について説明する.クォータニオンとは,この複素数を利用した回転表現の3次元空間への拡張であるので,この理解を避けてとおることはできないし,この理解が3次元空間の回転をより深く理解することにつながるはずである.
複素数とオイラーの公式
複素数と回転が関係すると言っても,なかなかピンとこないかもしれないが,ここでは,まず,一直線を表す数直線を示す.

当たり前だが,このように数直線は,図の左右の位置を表すことができる.
複素数と複素平面
次に複素数とは,実部と虚部を足し合わせたもので,例えば,
$${3+2 i}$$
は,実数で表した実部の3と,実数と虚数 $${i}$$ の積で表す虚部の$${2 i}$$ との和で表し,上で示した数直線はこの実部に相当する.ここで,虚数とはいろいろな性質を持つが,虚数の2乗は$${i^2=-1}$$となる性質を持つ.そこで,これを複素平面と呼ばれる実軸と虚軸の二つの座標軸で表すグラフで表示すると
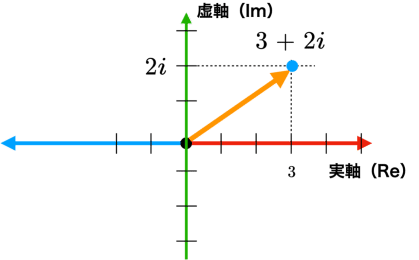
のように描画することができるが,これを一般化し,
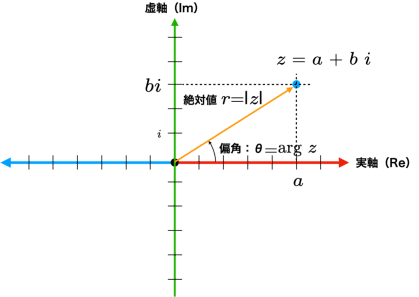
のように書き表すことができる.ここで回転角度は図3に示した偏角$${\theta}$$で表現できることに気がつく.
複素数と回転
複素数はこのように,実軸と虚軸に大きさを持つことができるが,回転を考えるだけなら,大きさが1の円を考えるだけで事足りる.せっかく,複素数の説明をしたところだが,ここから複素数を利用して回転について考ええいくので,以降,大きさが1の単位円に話を絞ることになる.これは,3次元の回転を考える場合,クォータニオンではなく大きさが1の単位クォータニオンで回転を表そうとしていることと理由は同じである.
そこで,虚部が0で,実部の大きさが+1である複素数をこの単位円上に書くと,
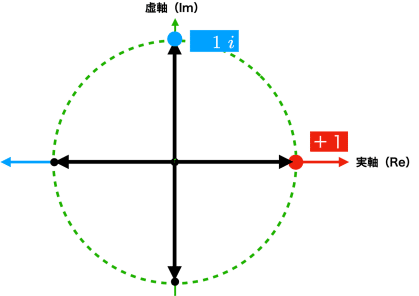
の赤色の点となる.次に,この「$${1}$$」に虚数 $${i}$$ をかけると「$${1 i}$$」 になる.ただし,ここではわかりやすく「$${1 i}$$ 」と書いたが,ただの「$${ i}$$ 」 と書けば十分である.
つまり,$${1}$$に虚数 $${i}$$ をかけることで,複素平面では単位円上を90度回転して,青色の点に移動することになる.つまり,虚数をかけることは,90度回転することに相当する.試しに,もう一度 $${i}$$ をかけると「$${-1}$$」になる($${i * i =-1}$$).つまり,$${i}$$ をかけることは複素平面の単位円上を90度回転することになる.このように

虚数をかけることが,複素数では回転を表現していることがわかる.
オイラーの公式
この単位円上の回転を数式で表したのが,有名なオイラーの公式となる.オイラーの公式は
$${e^{i\theta} = \cos \theta + i \sin \theta}$$
のように虚数を使用した指数(左辺)と,三角関数と虚数で表した右辺で表現されるが,この証明は「他に」譲り,この式の右辺に注目する.
この式の右辺の$${\cos \theta}$$は実部で,$${i \sin \theta}$$は虚部であるので,これは複素数であることはすぐにわかる.すると,この複素数の大きさは,$${\cos^2 \theta + \sin^2 \theta}=1$$ということがわかる.ここで,$${\theta}$$を前に取り上げた偏角とする.このように
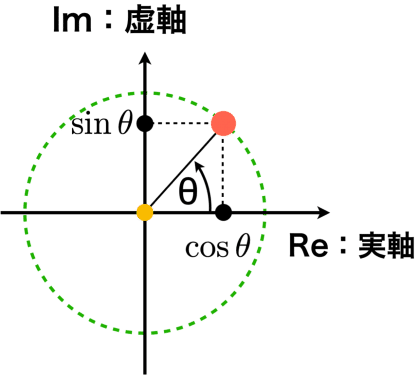
単位円上の点は,偏角$${\theta}$$を利用すれば,実部の$${\cos \theta}$$と,虚部の$${\sin \theta}$$で表現でき,虚数$${i}$$が回転を担っていることを示すオイラーの公式の右辺を図示することができる.オイラーの公式を用いれば,振動を美しく表現できるなど様々な恩恵を得られるが,我々の関心は回転の理解なので,ここではこの程度にとどめておく.詳しい説明は「ブルーバックス,オイラーの公式がわかる」などを参照されたい.
ここでの重要な結論は,平面の回転は「複素数」,さらにそれを使用した指数表現の「オイラーの公式」で単位円上の回転を表すことができるということに尽きる.虚数をかければ90度の回転を表し,オイラーの公式を使えば,平面の任意の角度$${\theta}$$も表現できる.
そこで,次に,いよいよ,このオイラーの公式によって表される2次元平面の回転を,3次元回転に拡張したロドリゲスの式について説明していくことになる.ロドリゲスの式でいかに3次元の回転を記述しているのだろうか...オイラーの公式とどのように似ているのだろうか...
参考文献
「オイラーの公式がわかる」ブルーバックス,原岡喜重著,講談社


【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
