
モーションにおける3次元回転 #10 〜平面角度の計算〜
バイオメカニクスの解析では身体や剛体の3次元回転の解析を行うよりも,「内外転角」や「回旋角」などの1自由度の回転角を解析することのほうが多いかもしれない.この1自由度の角度は平面内で記述される角度で,例えば,直線間のなす角度は2直線が形成する平面内の角度であり,直線と平面のなす角度は直線と平面が構成する面内の角度であり,回旋角度は回旋軸に垂直な面内の角度である.このように,ここでは平面内の1軸回転による角度を平面角度と呼ぶこととする.
解剖学で定義される関節角度も基本的には平面角度であるが,これにオイラー角を対応させて関節角度を表現しようとする方法もある.オイラー角は物体の3次元姿勢,すなわち回転行列を最小の3つのパラメータで表現する方法であるが,そもそも定義からオイラー角自体に幾何学的な意味を見出すことは困難であり,オイラー角の各パラメータを解剖学的関節角度に割り振っても解剖学的な角度の実態を反映しないので,関節角度をオイラー角で記述することを避けるほうが懸命である.
したがって,解剖学的関節角度の計算は,まずは身体各部位に固定された座標系の回転行列を利用し,座標系に固定された線と平面のなす角度などを算出するが,その計算では$${\mathrm{atan2}(y,x)}$$関数を使用することが基本で,逆余弦関数$${\mathrm{cos}^{-1}()}$$などの使用は,避けたほうが懸命である.$${\mathrm{atan2}(y,x)}$$については,4章
を参照されたい
モーションキャプチャを利用し,適切に貼付されマーカ群から角度計算の情報が得られるなら,わざわざ単位クォータニオンを算出する必要もなく,これらの計算は比較的容易である.モーションセンサ(IMU)の利用の場合は,様々な注意点があるので,この章では計測する上で注意すべき内容についても述べていく.
直交行列としての回転行列の復習
1.正規直交基底
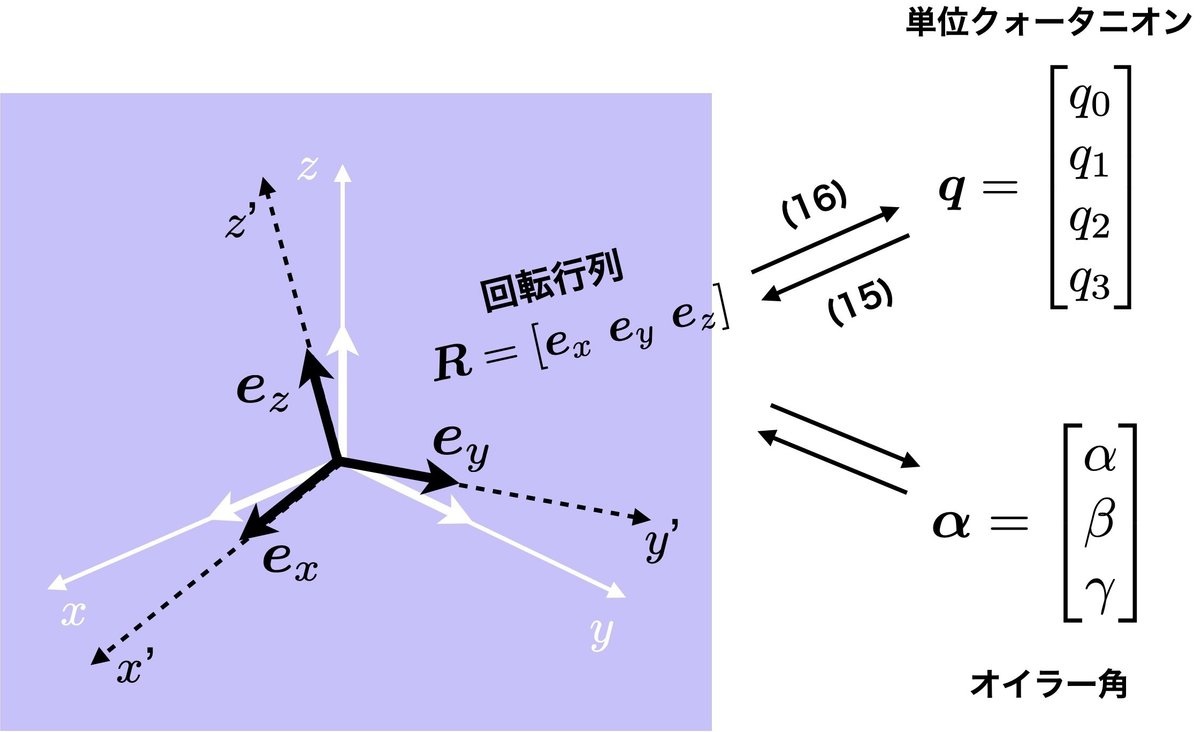
図1に示したように物体(剛体)の3次元姿勢は,物体に固定された直交座標系の各軸に固定された単位ベクトル$${\bm{e}_x, \bm{e}_y, \bm{e}_z}$$によって表される.この互いに直交する単位ベクトルは正規直交基底と呼ばれる.この正規直交基底を並べたのが回転行列で,これによって物体の姿勢(方向)を表すが,これが回転行列の幾何学的性質となっている.ただし,回転行列を基底$${\bm{e}_x, \bm{e}_y, \bm{e}_z}$$で記述する場合は,単に有向線分で表現する幾何ベクトルを並べているだけで,この記述方法では座標系とは無関係で成分は表れない.数学的な議論をするだけなら,成分表示せず可能な限り回転行列や基底だけで記述するほうがスマートな議論ができる.
しかし,いざモーションセンサやモーションキャプチャで物体の3次元姿勢(回転行列)を計測する段階となると,座標系の成分を記述する必要がでてくる.この成分は,座標系を指定しない限りは得らず,座標系と成分がセットであることに留意すべきである.
座標系が特に指定されていない場合の回転行列の成分は,通常は絶対座標系に対する成分がデフォルトの設定である.モーションキャプチャならモーションキャプチャで定めた(具体的にはキャリブレーションツールで定められる)絶対座標系に対する物体の姿勢であり,モーションセンサの場合は通常地面に対する姿勢である.この回転行列の各9成分は2章
で述べた方向余弦行列であり,この各成分は基準となる座標系の各軸の単位ベクトルと,物体に固定された各軸の単位ベクトルとの内積(方向余弦)という幾何学的性質を示している.
3次元回転と述べると,ついつい座標系を回転させるイメージを持つ.もちろんそのイメージによる理解は誤りではないが,正規直交基底や方向余弦による表現方法を用いると3次元回転とは「2つの座標系間の関係を座標系の各軸の単位ベクトルで表現」することなのだと気が付かされる.そして,その理解のほうが,幾何学的,数学的理解を豊かにしてくれることに留意すべきで,直交行列のそのような多様な性質を理解することで下記の理解も進むであろう.
2.回転のチェーンルール
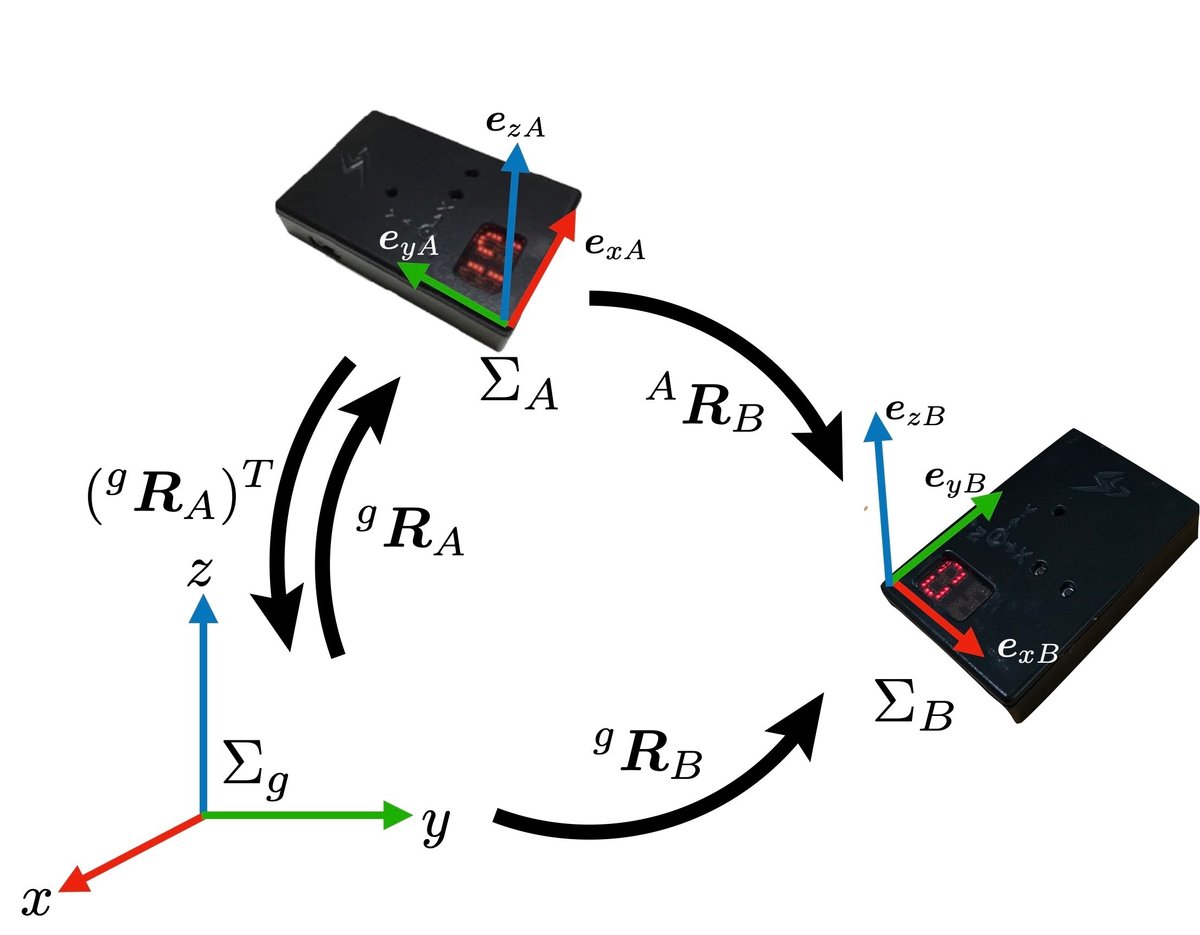
このことを別の例で少し詳しく考えてみる.座標系を記号$${\sum}$$で表し,図2に示すように絶対座標系$${\sum_g}$$から見た2つの座標系$${\sum_A, \sum_B}$$,すなわちそれぞれの剛体の姿勢を$${^g \bm{R}_A, ^g \bm{R}_B}$$と表すと,それらは次のように直交する各軸の単位ベクトル(正規直交基底)を横に並べて,
$$
^g \bm{R}_A = [\bm{e}_{xA}~\bm{e}_{yA}~\bm{e}_{zA}]
\\\\
^g \bm{R}_B = [\bm{e}_{xB}~\bm{e}_{yB}~\bm{e}_{zB}]
$$
のように記述でき,これは絶対座標系から見たそれぞれの相対姿勢となっている.たとえば回転行列$${^{g}\bm{R}_A}$$の場合,左上付の文字$${g}$$が「眺めている側」を,右下付記号$${A}$$が「観察されている側」の座標系を意味している.また,$${\bm{e}_{xA}}$$は絶対座標系$${\sum_g}$$から見た座標系$${\sum_A}$$の$${x}$$軸方向の単位ベクトルを示している(図2参照).
次に,座標系$${\sum_A}$$から見た,座標系$${\sum_B}$$の相対姿勢を考える.たとえばモーションセンサで身体運動を計測する際に,体幹に固定されたセンサ座標系からみた腕のセンサ座標系の相対姿勢(回転行列)を計測するときにこのような計算が必要となる.すなわち,座標系$${\sum_A}$$から見た座標系$${\sum_B}$$の姿勢は,2章の方向余弦の考え方から座標系$${\sum_B}$$と座標系$${\sum_A}$$の各軸間の内積(方向余弦)を計算すればよく,
$$
^A \bm{R}_B=
\begin{bmatrix}
\bm{e}_{xA}^T \bm{e}_{xB} & \bm{e}_{xA}^T \bm{e}_{yB} & \bm{e}_{xA}^T \bm{e}_{zB} \\
\bm{e}_{yA}^T \bm{e}_{xB} & \bm{e}_{yA}^T \bm{e}_{yB} & \bm{e}_{yA}^T \bm{e}_{zB} \\
\bm{e}_{zA}^T \bm{e}_{xB} & \bm{e}_{zA}^T \bm{e}_{yB} & \bm{e}_{zA}^T \bm{e}_{zB}
\end{bmatrix}
\\=
\begin{bmatrix}
\bm{e}_{xA}^T \\ \bm{e}_{yA}^T \\ \bm{e}_{zA}^T
\end{bmatrix}
[\bm{e}_{xB}~\bm{e}_{yB}~\bm{e}_{zB}]
\\=
\left(^g \bm{R}_A\right)^T ^g \bm{R}_A\qquad\qquad
\\=
^A \bm{R}_g ~~^g \bm{R}_A \qquad\qquad(1)
$$
となる.
このとき,図2の$${^A \bm{R}_B}$$は$${\sum_A}$$から$${\sum_B}$$に向かう最短の矢印を指しているが,$${\sum_B}$$に向かうためには$${\sum_A}$$から$${\sum_g}$$を経由して$${\sum_B}$$に到達するルートもあり,最短ルートとその2つの矢印経由で回転させるルートと回転の意味では等価であることを示している.そして,これは,式(1)において最初の回転$${\left(^g \bm{R}_A\right)^T = ^A \bm{R}_g}$$の右側に,続きの回転である$${^g \bm{R}_A}$$を掛けることで$${^A \bm{R}_B}$$を計算できることに相当している.
これを一般化するなら$${\sum_A \rightarrow \sum_B \rightarrow \sum_C \rightarrow \sum_D \rightarrow \sum_E}$$の順で回転させる場合は,
$$
^A \bm{R}_E =
^A \bm{R}_B ^B \bm{R}_C ^C \bm{R}_D ^D \bm{R}_E
$$
の順番で回転行列を右側に掛けていけば良く,これはチェーンルールと呼ばれる.身体の場合は,体幹→上腕→前腕→手,のように繋がっているので,右側に相対姿勢変換(回転行列)を掛けていけば,体幹から手先の姿勢に変換する合成の回転行列を計算できるということを示している.
3.オイラー角による解剖学的関節角度表現
なお,身体の3次元姿勢を特にモーションキャプチャなどの光学系計測機器で身体の各部位の座標系を定める場合は,身体各部位のマーカの貼付の仕方等による座標系の定義に依存するので,それらはISB(International Society of Boimechanics,国際バイオメカニクス学会)などの標準化された定義(文献1参照)などを利用するとよいであろう.
その際,3次元姿勢を表す回転行列は9個のパラメータで表現されるため,実際に数値計算をしたり,センサで成分を出力するには情報が多すぎる.そこで,できるだけ少ないパラメータで3次元姿勢を表現するニーズが生まれ,これまで多用されていたのがオイラー角などの最小の3つのパラメータで表現する方法である.ただしオイラー角については,多くの教科書などで取り扱われており,またバイオメカニクスの解析において単位クォータニオンの使用を推奨する立場から,ここでのオイラー角の説明は割愛する.
なお,図1に示したように回転行列と単位クォータニオン間は9章の式(15)(16)で変換できる.また同様に,オイラー角についても同様な変換は可能である.ここで注意が必要なのは,これらの変換によってもちろん単位クォータニオンとオイラー角間でも変換が可能であるが,これらの変換では必ず回転行列を経由して計算していることを意識したい.また,3次元回転の数学的な性質を拘束するのは回転行列で,回転行列の数学的性質を直交行列が定めている.その直交行列としての重要な性質は,この「モーションにおける3次元回転」では割愛したので,文献2などを参考に勉強していただければと思う.
解剖学的関節角度の計算
解剖学における角度定義は,数学的には曖昧な角度定義が多い.たとえば肩関節を例に考えると,数学的には回転の自由度は3自由度しかないのだが,伸展屈曲,内外転,内外旋,水平屈曲伸展と,4つの回転が存在する.また,これを無理やりオイラー角に割り当てて表現しようとするISBの標準化方法もあるが,オイラー角自体に物理的な意味がないのでそもそも無理があり,筆者は適切な方法ではないと考えている.
そこで,ここでは一般的な定義とは異なるかもしれないが,解剖学的角度の定義を考える.すなわち,身体の各部位に固定された座標系の3次元姿勢,すなわち3次の回転行列が既知の場合,どのように1自由度の角度を計算すればよいのかを考えていく.
角度算出の注意点
図3のように緑の矢印で示された軸と,基準面としての水平面とのなす角度は逆正接関数$${\rm{tan}^{-1}()}$$を計算することになるが,前章でも述べたように,プログラミング言語のatan2(y,x)を使用することで,符号付きで,かつ精度良く角度を算出できる.可能な限り,$${\cos()}$$の逆関数$${\cos^{-1}()}$$は使用しないことである.
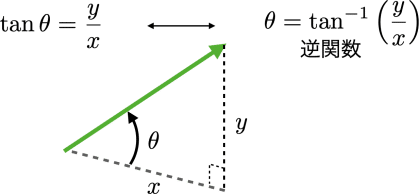
例1:座標軸と水平面のなす角度
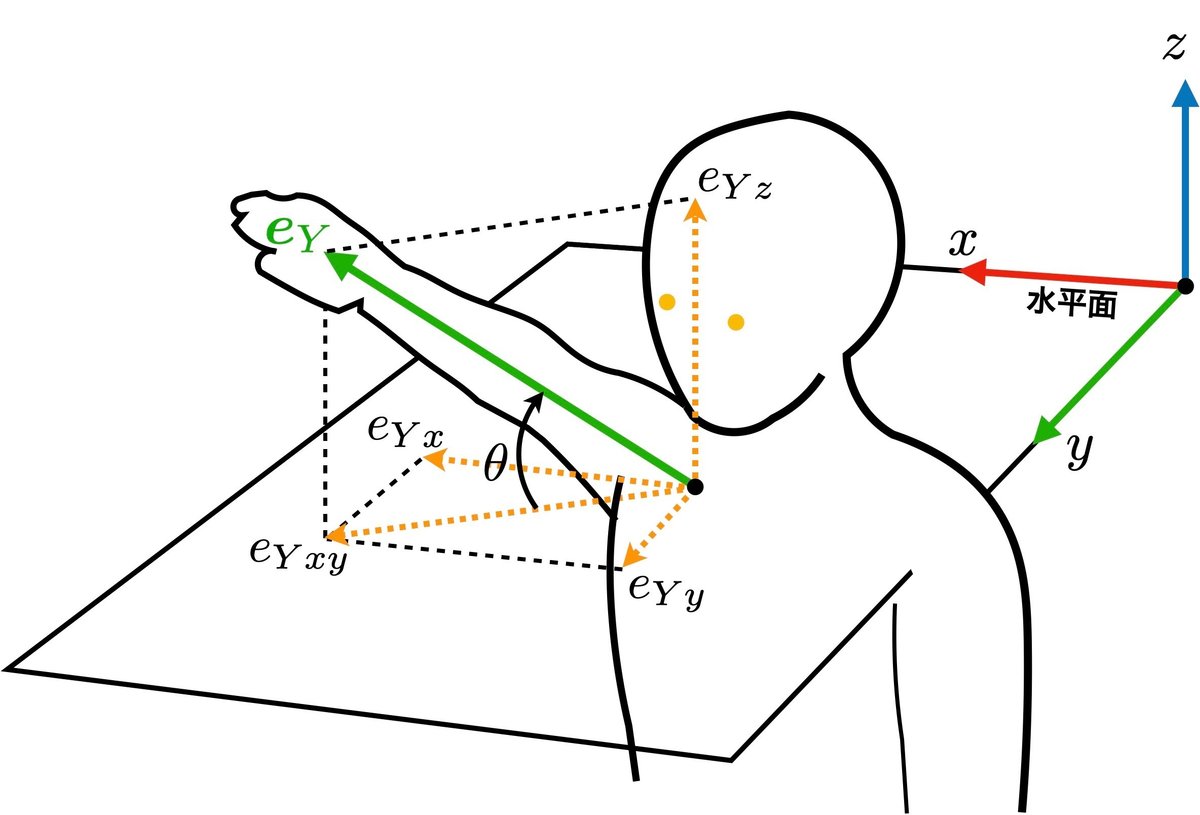
ここでは,図4のように上腕の長軸に,上腕のローカル座標系のY軸とを一致させ,その長軸と基準面としての水平面となす角度を計算する.このためはY軸の基底(単位)ベクトル$${\bm{e}_Y}$$と水平面となす角度を$${\mathrm{atan2}(y,x)}$$関数から計算すればよいので,引数$${y, x}$$として,$${\bm{e}_Y}$$の鉛直方向成分$${e_{Yz}}$$と水平成分$${e_{Yxy}}$$を与えて,$${\mathrm{atan2}(e_{Yz}, e_{Yxy})}$$ として角度を与える.ここで$${e_{Yxy}}$$は図4から
ここから先は
¥ 100
