
直感を信じて【定積分計算:横浜国立大】
今回は、横浜国立大の定積分計算です。問題はこちら。

分母が気になりますね。まずは、直感として三角関数の合成が思いつきますが、これでいいのかなという不安もありますね。
このようなときは、ある程度まで追っかけて、ダメだったら撤退、行けそうなら継続でいいのかなと思います。
まずは分母を合成をしていきましょう。

では、このまま組み込みます。分母にsin(x+α)の式がでてきましたので、次のような変形が見えることが望ましいでしょう。

これでt=cos(x+α)とすれば、置換積分として処理できそうですね。
置き換えた式の微分が存在するからです。

ここまでくると部分分数分解ですね。
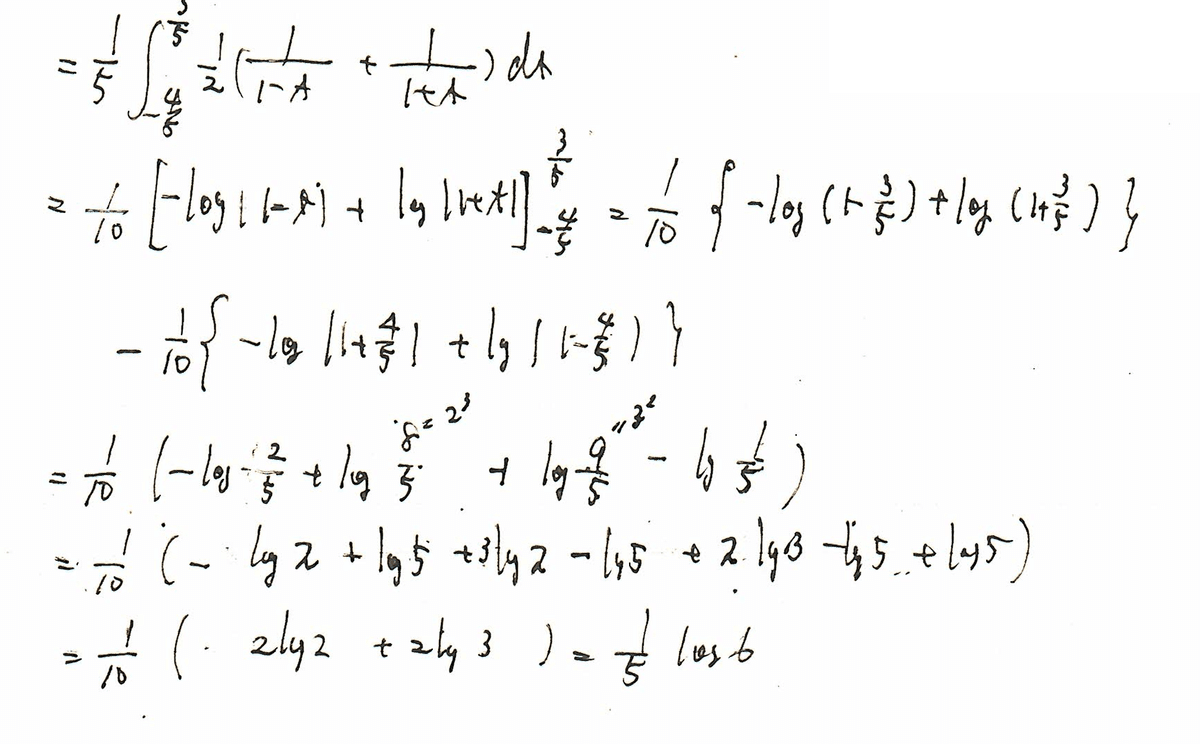
無事計算ができました。
対数の因数が分数でちょっとチラチラしますが丁寧に処理していけば割とすっきりしとした解になりました。
積分計算は、このようなちょっと変わった形に出会うことがあります。経験がものをいうところですので、こういう機会を大事にしてくださいね。
