必要十分条件から発想するとは？（共通テスト試行調査：ベクトル）

今回は共通テストの試行調査の問題です。

ベクトルは、攻めている印象のある共通テスト。２０２１年は、正十二面体が登場し、受験生をビビらせました(・.・;)

ベクトルは、パターン化が顕著という事情もあり、受験生を揺さぶる方向にあるのでしょうね。

その象徴のような問題だと感じているのが、こちら

（１）～（２）までの流れは、

となり、（３）が受験生を揺さぶりにかけていますね。

表題にある通り、（２）で必要十分条件を求めさせて、（３）で活用させています。

ここで出題者のメッセージを読み解く必要があります。

受験生の混乱をよそに、選択肢があまりにシュールですね。

論理のつながりがブラックボックスというセンター試験時代からの伝統は共通テストでも引き継ぐよ！という宣言なんでしょうか。

頼れるのは、必要十分条件だけです。

とは言うものの、これだけをじっと見つめていても解決しません。

ここから、必要十分条件を拡張していきます。ここで大事なのは、内積の式を、定義に基づいて変形するのは、何の問題もないということです。

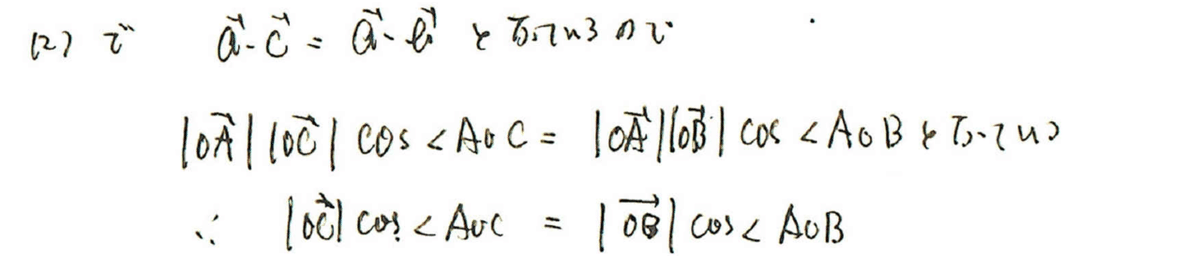
となりますね。共通のOAベクトルの大きさの式は、カットしてもよさそうですね。

これから何が言えるのかと発想します。

当然

ですね。

よって、

が正解とわかります。

大事な点は、２つです。

必要十分条件から発想すること。

定義に従って式変形すること。

・・・です。本問はこの二つが解法の鍵になっています。

共通テストは、このあたりの思考法を大切にしているところがありますね。より論理的になっているように感じるところでもあります。

対処療法的な発想では通用しない問題の一つでしょう。しっかりと確認しておいてほしいポイントかなと思います。