九州大理系数学２０２３年解説【［２］極限　「実験」によってイメージを出し、示す方向性を決める】

今年の九大の入試問題の解説をアップしていきます。
前回はこちら。

今回は理系数学［２］極限の問題です。
問題はこちら。

漸化式と極限の融合問題ですが、実質は極限の問題ですね。（３）と（４）は、検証を丁寧にやらんとヤバいのかなという予想が立ちそうな問題ですね。実際の採点がどうだったのかが気になりますが、（１）（２）の部分点食い逃げ戦略は、結構厳しくみられたかもですね。

まずは漸化式の絶対値を処理します。

aｎが（ⅰ）ならば当然ｎ→∞で０に収束しそうですね。
（ⅱ）は漸化式を解くと

となるので、αー２＞０ならばｎ→∞で∞に発散することが言えそうです。

（１）、（２）は、αの範囲を考えるとまずはこれだけの分析で答案が書けそうですね。

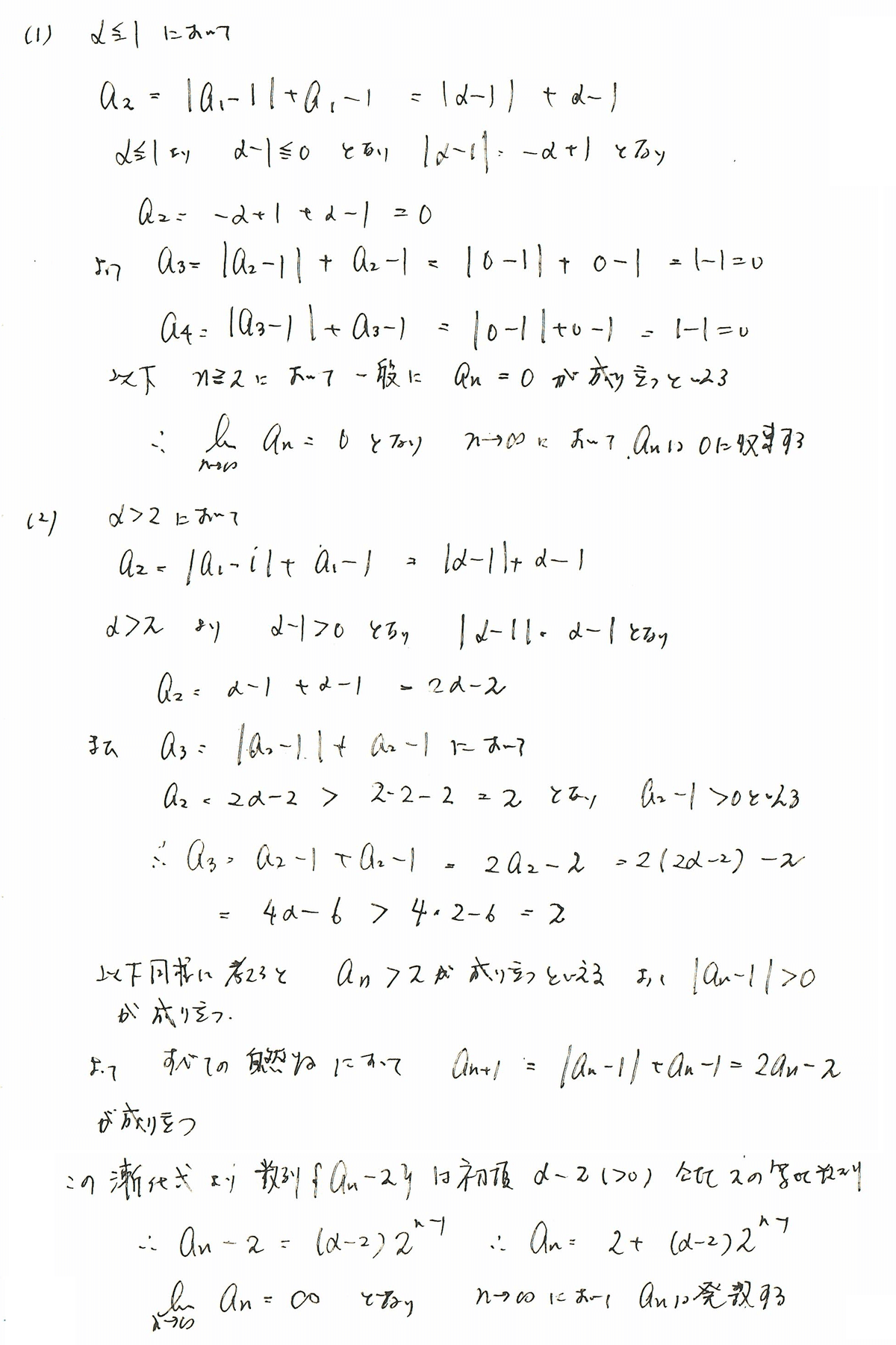
問題は（３）と（４）ですね。αが３/２を境に何かが変わるのかなと予想ができそうですが、実際に調べないと何が起こっているのかはわからないので、頑張って「実験」しましょう。

（３）は案外早い段階で、aｎ＝０が見えましたね。食わず嫌いで（２）で打ち切った受験生はちょっともったいなかったかもですね。

一方、（４）は、ー１≦a３ー１＜１の解釈がポイントでしたね。
確実に　|　a３ー１　|　＞０が言えないことを
👇
「ある」自然数ｎにおいて、aｎ≦１を満たすaｎが存在すると読み替えることができたかどうかでしょう。

これが見えると
「すべての」自然数ｎおいて、aｎ＞１の矛盾を導く背理法による証明が見えてきます。

よって（３）は、

となり、
（４）は、

となりそうですね。
医学部医学科以外は、（３）まで、医学部医学科は（４）までは取りたい問題だったかなと思います。

本問、予備校の評価が割れましたね。駿台、河合塾は「難」とし、代ゼミは「標準」。自分はその中間の「やや難」かなと思いつつ、代ゼミの先生の見解を支持する感じですね。