VALORANTで学ぶ数学 ～ネオンのスライディングショットが頭に当たる確率～

　前回このような記事を投稿し、割と好評な感じの反応をいただきました。

今回はこの記事の練習問題編みたいな感じでネオンのスライディング時における弾の拡散率を求めます。なお、ご自分で求めてみたい方は是非解いてみてください。条件は以下に記載します。

敵と目が合っている状態で、敵の頭の真ん中に初弾を撃つという前提のもとに計算する。
頭の大きさ…縦0.34 (m)、横0.17 (m)の長方形 [1]
敵と自分の間隔…30 (m)
1ST SHOT SPREAD…1.05 (DEG/ADS)

どうでしょうか？しばらくは計算の本題に入らないので、ここら辺を見ちゃっても大丈夫だとは思いますが、事故防止のためにまえがきをいろいろ書きます。これらについて一般化まで考えられる人は是非それについても考えてみてください。それでは、始めていきましょう。

頭の大きさを求める

Explaining the hit registration and latency problems in Valorant

　今回、VALORANTにおける頭の大きさを求めるにあたってこちらの記事を参考にしました。ありがとうございます。

スライディングショットで頭に当たる確率を求めるうえで必要な値は、頭の大きさとスライディング時の拡散率です。まずは頭の大きさですが、参考文献にある画像から縮尺を利用して求めます。

エージェントの大きさ、箱の高さと一緒

一般に、VALORANT内のそこら中にある立方体の箱型オブジェクトの高さは、VALORANTにおけるヘッドラインと一致するとされていて、実際に確認してみてもその通りになっていることが上の画像からもわかります。そしてこれらの立方体の箱は1辺が2mほどの長さであることが知られており、エージェントの全長が2mであることがわかります。

縮尺から頭の大きさを計算する、なんか線が斜めだな…

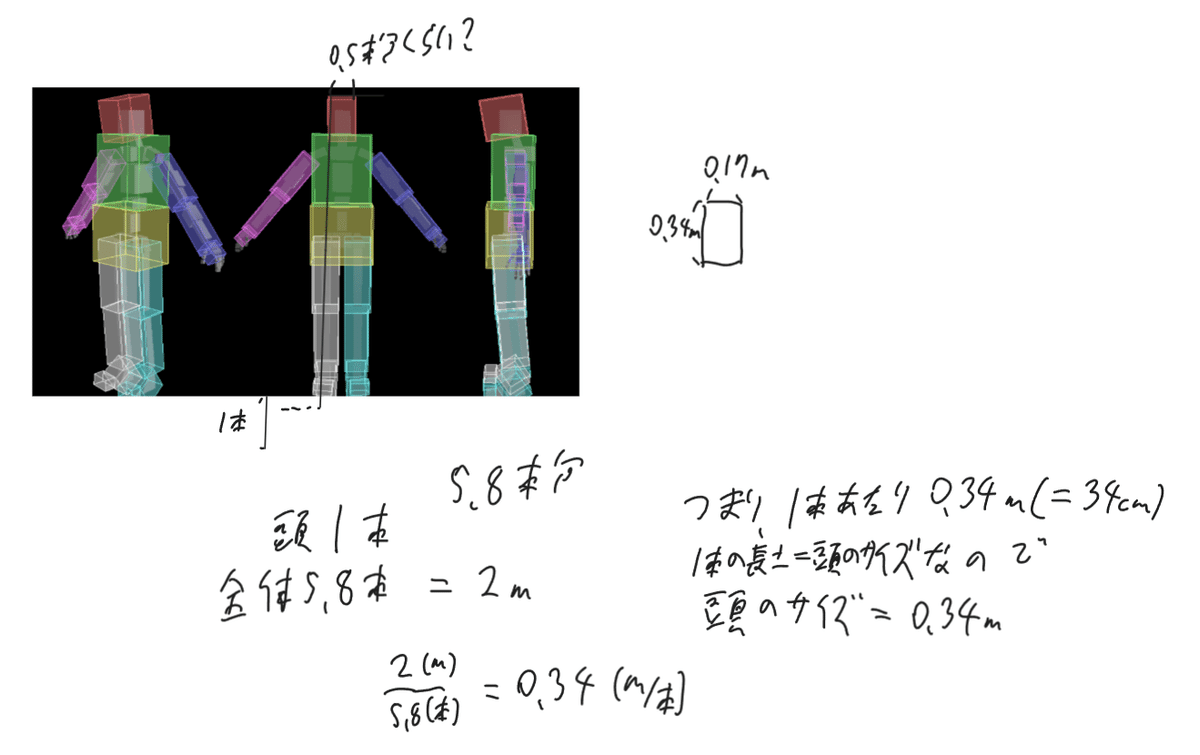
最初に縮尺を用いて数値を出すと書きました。今回はエージェントを正面から見た図を用いてエージェントの頭と全体それぞれに線を引き、その長さを比べることで頭の大きさを求めました。また今回は単に線を引くのではなく頭に線を引いてからその線を複製し何本分になるかを測定しました。実際に線を引いてみたところ、頭に引いた線1本に対して全体の長さは5.8本分になりました。エージェントの全長は2mであったので、長さ÷本数という式から1本あたりの長さが求まります。計算結果は画像の通りで2/5.8=0.34 (m/本)であり、1本の長さはそのまま頭の長さであるため頭の長さは0.34mであることがわかります。横も同様に計算すると0.17mになり頭の大きさが求まります。

ネオンのスライディング時における拡散率

　これはどちらかというとVALORANTの仕様を知っているかどうかですね。実はVALORANTにはプレイヤーがストッピングできてるか・タップが適切かを判別できるグラフを表示させる機能があります。

ビデオ設定のSTATSの一番下

VALORANT内での表示、黄色の数字があるとこ

しゃがみ歩き時ヴァンダル初弾のShooting Error

　画像の通りです。黄色いところが射撃エラーで青いところが移動エラーになっていて、例えば走り撃ちをすれば青い部分が伸びてフルオートをすれば黄色い部分が伸びます。そして実はこのShooting Errorの単位も1ST SHOT SPREADと同じく度数法が用いられています。3番目の画像はしゃがみ歩き撃ちでヴァンダルの初弾だけを撃った時のグラフです。黄色の部分がヴァンダルの1ST SHOT SPREADになっていて0.25°、線の長さは1.05°と表示されていて、ネオンのスライディング時における精度はしゃがみ歩き時と同じ値なので、0.80°がスライディング時における移動エラー、これにそれぞれの武器における射撃エラーを追加した値がスライディングショットでのShooting Errorになることがわかります。

計算してみよう

　前回同様、今回の状況を簡単に図に起こしてみましょう。

頭の真ん中に撃つ

繰り返しになりますが、頭の真ん中を狙って撃つという前提で計算します（わりと重要）前回の三角関数式を用いればどのくらいずれるかはこの図から明らかです。

30tan(1.05)≒0.55m

簡単ですね。そういえば完全に言い忘れてたんですが、三角関数の計算をするときはお手元の関数電卓で計算してください。1.05と入力してからtanというボタンを押せばtan(1.05)の値が出力されます。
そして今回はここで終わりません。前回もここでも銃弾が真上に跳ねることだけを想定していましたが、実際には360°全方向に弾はずれます。

色んなとこにずれる

自分の撃ちたい方向から1.05°ずれて全方向に向かうということは、弾の拡散する範囲が円形に広がるということです。

弾が拡散する範囲

こんな感じに、しゃがみ歩き撃ちでヴァンダルの初弾が着弾する範囲はこの円のどこかになるということです。この円と頭の当たり判定を重ねてみましょう。

頭の当たり判定と弾が当たる範囲

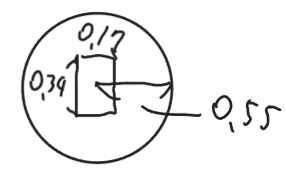
そして、弾が当たる部分を赤くしてみるとこんな感じです。

赤い部分が弾の当たる範囲

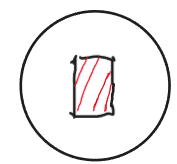
最初に求めたかったはずの結論をついに出しましょう。スライディングショットが頭に当たる確率は、弾が拡散する範囲の面積に対する当たり判定の面積を求めればいいことがわかります。つまり、赤色の面積÷円の面積によって求まります。赤色の面積は0.34×0.17=0.0578、円の面積はπ×0.55×0.55=0.95…、よって確率は100・(0.0578/0.95)=6%、となります。

一般化しよう

好評だったらやります！！！！！疲れたので

あざっした～