
逆行列を空間的に理解する
このnoteについて
このnoteは私が初めて書くnoteです.
このnoteは画像と少しの文で構成されているのでとても見にくいと思います.
私の文は句読点の位置がとてもおかしなところにあると自覚があります.
そのため,句読点の位置の間違いを指摘してくださると幸いです.
逆行列とは
逆行列,それはとても難しいものである.
正則行列Aに逆行列$${A^-1}$$を掛けると$${I}$$(単位行列)になるというものである.
行列式の公式として余因子行列掛ける行列式の逆数.
$${A^-1=\frac{1}{det A}A^~}$$
$${A^~}$$はAの余因子行列
とても理解できるものではない.
そのため,逆行列がどのようなものか簡単に理解するために2次元平面と3次元空間上でどのように逆行列が働いているか見てみる.
その前に
内積とは
内積とはベクトルを合成したときにどのくらい変化したのかを表す指標である.ベクトル同士が同じ方向を向いていると大きく,反対の方向を見ていると小さくなり,そのどちらでもない,垂直の場合は0になる.
内積の公式は$${\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta}$$
$${\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2:a_1,b_2}$$などはベクトルの成分
ここで大事なのは$${cos(90^\cric)}$$のときは内積は0になるということ.
行列の積とは
行列の積の解釈はいろいろあるがここでは,内積に注目したいと思う
行列の積は
$${\begin{pmatrix}a_1&a_2\\a_3&a_4\\\end{pmatrix}\begin{pmatrix}b_1&b_2\\b_3&b_4\\\end{pmatrix}=\begin{pmatrix}a_1b_1+a_2b_3&a_1b_2+a_2b_4\\a_3b_1+a_2b_3&a_3b_2+a_2b_4\\\end{pmatrix}}$$
と表せる,ここで注目してほしいのが$${a_1b_1+a_2b_3}$$などの行列の要素が前節で紹介した内積の公式に似ていることがわかる.
内積の公式を使用するためには$${(a_1,a_2)(b_1,b_3)}$$と考えればよく,左辺の最初のaの行列は行方向(横)にベクトルを作り$${(a_1,a_2)(a_3,a_4)}$$
次の行列bは列方向(縦)にベクトルを作ればよい$${(b_1,b_3)(b_2,b_4)}$$
これで行列をベクトルの内積として計算することができる.
2次元平面で見る逆行列
では,2×2行列の逆行列を求めていく.
$${\begin{pmatrix}1&2\\3&4\end{pmatrix}}$$
この正則行列を例に逆行列を平面上で見ていこう.
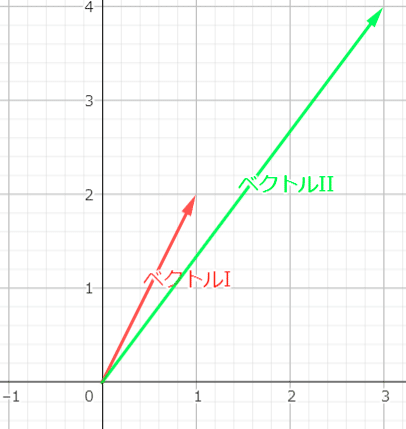
まず,この行列は(1,2)(3,4)のベクトルが2つ同じ平面上にあると考える.
ベクトルIが(1,2),ベクトルIIが(3,4)

次に,ベクトルIIに対して垂直に交わる直線を引く

すなわち,直線上にベクトルが存在するならば,そのベクトルとベクトルIIの内積は0ということを示している.
しかし,ベクトルIとの内積は0にはならない.
ということは,この直線状にいい感じにベクトルを取ってあげればベクトルIとの内積が1にできるということである.

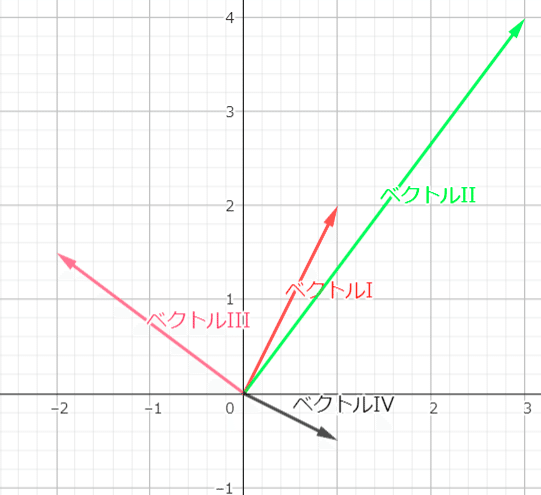
このようにいい感じのベクトルIIIを生み出すことに成功しました.
次はベクトルIとの内積が0でベクトルIIとの内積が1になるベクトルを同じ操作で生み出します.
このようなベクトルが合った時
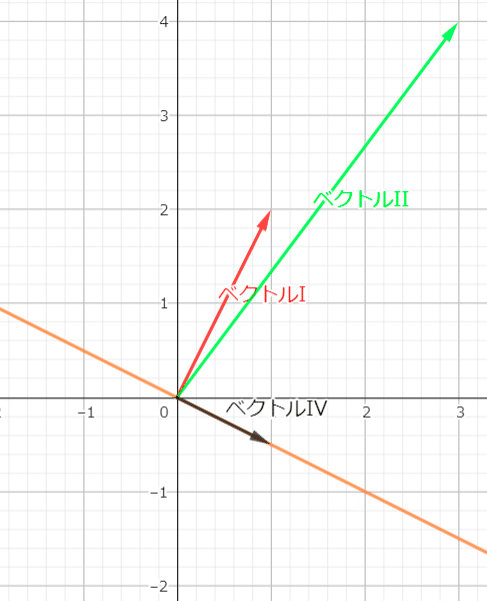
ベクトルIに対して垂直な直線を作る.

次にその直線状にベクトルIIと内積が1になるベクトルIVを作る.
出来たベクトルを縦に並べて行列をつくる.
$${\begin{pmatrix}-2&1\\\frac{2}{3}&-\frac{1}{2}\end{pmatrix}}$$
このような行列になり,この行列が逆行列となっている
3次元空間で見る逆行列
3次元のため3×3の行列の逆行列を求めたいと思う.
やり方は2次元のときとほとんど変わらないがなぜ,正方行列のみが逆行列を取るのかがわかりやすいと思う
今回例として使用する行列は
$${\begin{pmatrix}1&2&3\\4&0&2\\2&1&0\end{pmatrix}}$$
となっている.この行列の行成分をベクトルとして3次元空間にプロットしたものが下図である.赤がx(1列目)緑がy(2列目)青がz(3列目)





想像しにくいかもしれないがその時はGeoGebraを使用して確かめてほしい
基本的にしていく作業としては2次元平面のときと変わらないが2次元平面のときは,あるベクトルと内積が0になるのは直線を引いていたが3次元空間では内積が0になるのは平面となる.
ここで,ベクトルIIと内積が0になる平面を作ってみる.

次にベクトルIIIに対して内積が0になる面を作っていく.

このとき,2つの面が重なっているところはベクトルIIとベクトルIIIどちらの内積も0になる.そのため,重なっているところにベクトルIとの内積が1になるベクトルをれば良い

小さいが2つの面に重なっているかつベクトルIと内積が1のベクトルIVを作ることに成功した.
これをあと2回繰り返す
繰り返した結果このようになった

これを縦に並べたものが逆行列である
$${\begin{pmatrix}-\frac{1}{9}&\frac{2}{9}&\frac{2}{9}\\\frac{1}{6}&-\frac{1}{3}&\frac{1}{6}\\\frac{2}{9}&\frac{5}{9}&-\frac{4}{9}\end{pmatrix}}$$
このように2つのベクトルには垂直にもう1つのベクトルに対しいい感じの長さに調整するのが逆行列です.
逆行列が空間でどのように配置されてるかわかっていただけただろうか.
最後にフォローはいいからいスキして
ここまで読んでくださりありがとうございます
