【数学】対戦ゲームにおける「レート2000」とは

ゲームをしている方なら何度か、あるいは毎日「レート」という言葉を耳にすると思います。レート1500でスタートし、レート2000という数字を目標にするプレイヤーはゲームタイトル問わずガチ勢界隈では多いのではないでしょうか。所謂レーティング対戦の主軸となっているこの数字をこれから噛み砕いて説明していこうと思います。

イロレーティングっていうらしい

本文で説明するレーティングシステムはアメリカ人物理学者でありチェスガチ勢のアルパド・イロが考案し1960年にアメリカ合衆国チェス連盟に採用されたイロレーティングシステムというものです。

この方法はチェス、囲碁、将棋、麻雀などのオンライン対局場ではもちろん、ポケモンのレート戦、スマブラのネット対戦など多くのゲームで用いられるレーティングシステムです。

相手のレートから自分の勝率を求める

始めにイロレーティング、通称レートとは一言で言うと勝率の指標です。つまり自分と相手のレートを比べることで自分の勝率を導き出すことが出来ます。

では、レート1500のプレイヤーと対戦した時の勝率が自分のレートによってどう変動するのかをまず見てみましょう。

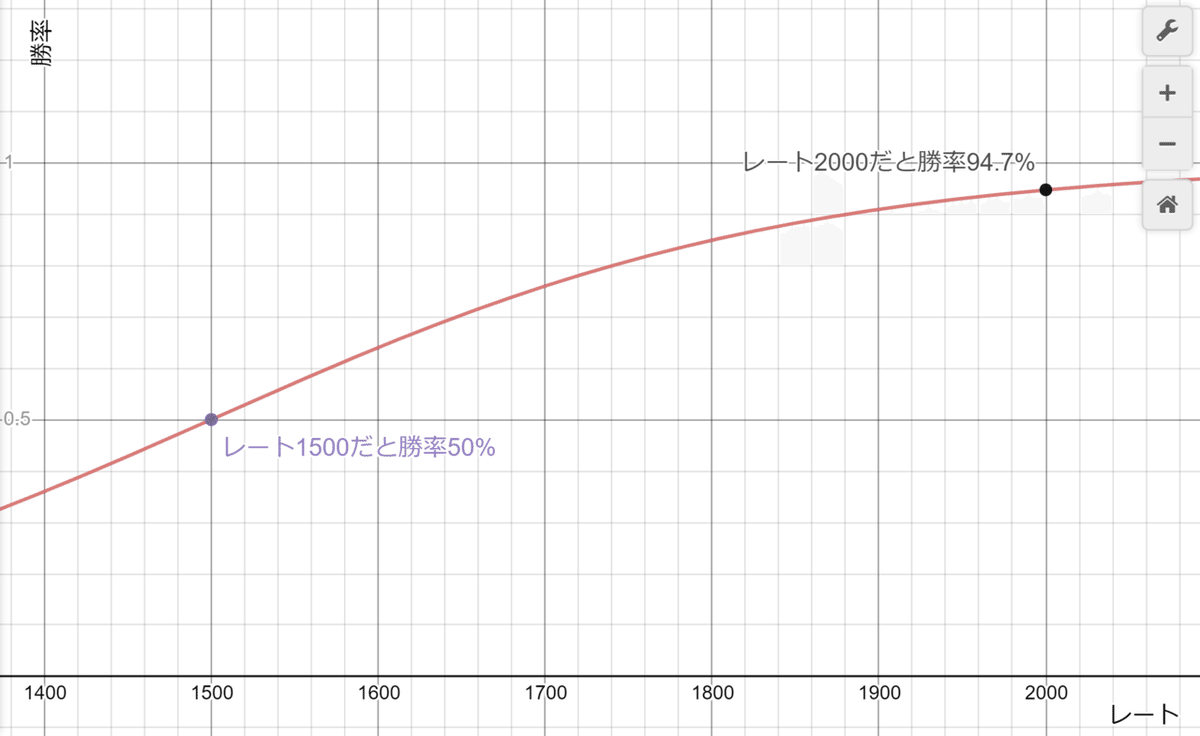
ｘ軸が自分のレート、ｙ軸が勝率となっています。

グラフを見ると、自分のレートが1500なら同じレート1500の相手と対戦した場合に勝率50％、半々という事になります。数値的にはまったく同じ強さという事になるので納得ですね。自分がレート2000なら勝率はおよそ95%になります。ほぼ勝ち確。

では相手のレートが1600だった場合はどうでしょう。

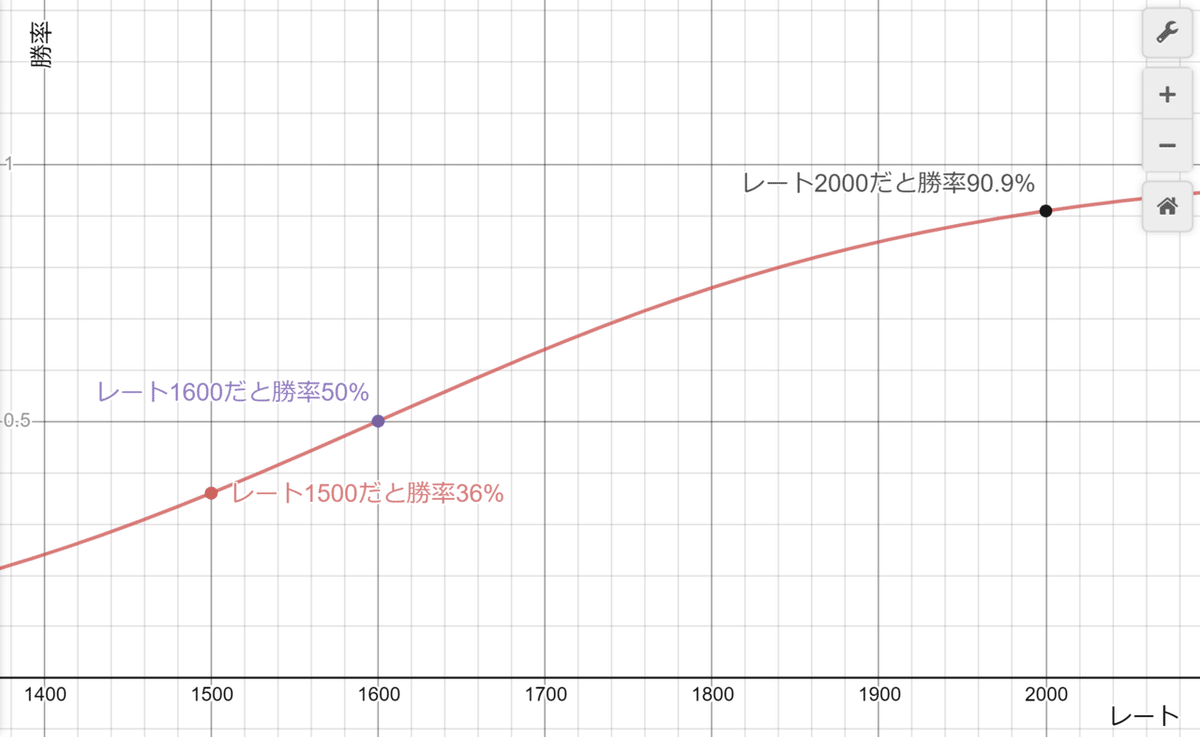
先ほど通り自分も同じレート1600なら勝率50％。1500なら負け予想、2000なら先ほどに比べて少し下がり気味の91%程度です。

対戦相手はレート1800...勝率は？

で、さっきのグラフはなにが元になってるんだ？っていう話ですよね。これがイロレーティングシステムの根幹です。ちょっと数式が入ってきますが難しくないので行かないで！

自分の勝率をEᴀ、自分のレートをRᴀ、そして相手のレートをRʙとして

で定義されます。

なんこれ？

と思うかもしれませんが、数式なんてパッと見大体そんなもんです。

先ほどのグラフに沿って考えてみましょう。自分と相手が同じレートだった場合()の中の Rʙ-Rᴀ はゼロになります。10のゼロ乗は1なので Eᴀ=1/(1+1)=0.5 となります。グラフ同様、勝率半々です。

今度は自分のレートを仮に無限とした場合はどうでしょう。10の‐∞乗は0なので今度は Eᴀ=1/(1+0)=1 となります。といったように相手と自分のレートの差が無限に近づくにつれ勝率が100％に近づくことが分かります。

もう一つ分かるのは勝率は自分と相手のレートの差しか関係ないということ。レート1500が1600に勝つ確率はレート2000が2100に勝つ確率と同じということです。

となると対戦相手がレート1800というだけでは勝率は求められません。仮に自分がレート1500だとすると数式に当てはめ

勝率はおよそ15％となります。

クッソー負けたわー...レートはどんだけ落ちる？

さてここで本題、レート変動について。どうやったらレート1500からレート2000に到達出来るのか？自分よりレートが高い人に勝てば上がるし、自分よりレートが低い人に負ければ下がるっていうのは分かっても他の場合は？自分よりレートが300も高い人に負けたら、どのくらい落ちる？レート戦やってる人なら感覚で分かると思いますが、ちょっとだけ落ちます。

では一体どれだけ落ちるのか？

先ほど計算した勝率Eᴀと実際の勝率を比べます。実際の勝率をWとし、値を勝てば1、負ければ0とします。予想のEᴀがWと違えば違うほどレートの変動が大きくなるわけです。

これがイロレーティングシステム。

変動後の新しい自分のレートをRᴀ'として

と定義します。単純に Rᴀ'=Rᴀ'+W-Eᴀだと一生1500のままなので（WもEᴀも常に1以下なので）Kという定数で変動を大きくします。このKは一般的に32とされています。

では実際に変動を計算してみましょう。レートが自分より300上の相手に勝てる確率は先ほど計算した通り15％です。

実際に負けた場合はW=0になります。そうすると、

という風に約5ポイント下がる事が分かります。因みに勝てば約27ポイント上がります。もちろんKの値が変われば変動値も変わってきます。

レート2000にたどり着くまで

ここまでお付き合いいただきありがとうございます！最後にレート2000がどれほどのものなのかというのをちょっと検証してみたいと思います。

まず、相手のレートを固定した場合と1400~2000の相手にランダムに当たった場合の全勝を仮定としたレート2000までに必要な対戦数。

全勝する実力があれば案外すんなり2000入り出来ちゃうわけですね。もはやすんなりではないか。。。

他にも麻雀などの4人制ゲームでのイロレーティング方式、K値の求め方、イロレーティングのインフレ・デフレ問題など色々ありますので興味があればコメントなどよろしくお願いします。