
九九の図に分数の足し算を感じる
「図にすると美しい九九の世界」というのが2017年あたりに話題になっていた。
九九から下記のような図が作れるといった話だ。

九九の図 (-, 10)を一般化すると、 (-, 2)や(-, 5)の図が描ける。
実際に描いてみれば、(1, 5)と(2, 10)が同じ図になることがわかるだろう。

他にも、(2, 5)と(4, 10)、(1, 2)と(5, 10)、(3, 5)と(6, 10)、(4, 5)と(8, 10)が同じ図になる。
なんだか約分のような雰囲気がある。
念のために列挙すると1/5 = 2/10、2/5 = 4/10、1/2 = 5/10、3/5 = 6/10、4/5 = 8/10だ。
1/5 の分母分子に2を掛ければ 2/10 になるが、これは形式的な通分でも起こる。
1/5 = 0/2 + 1/5 = (5×0 + 2×1) / (2×5) = 2/10
ところで 1/2 + 1/5 = 7/10 だが、この類推から(1, 2) + (1, 5) = (7, 10)と考えてみたい。
すると、次のように足し算の表が埋まる。
ただし、(1, 2) + (3, 5) = (11, 10) = (1, 10)である。
帯分数の整数部分を忘れるイメージだ。
1/2 + 3/5 = 11/10 = 1 + 1/10

この図の足し算を、2つの周期的な整数列から別の周期的な整数列を作る演算だと思ってみたい。
$${(a, b)_n = a n \text{mod} b}$$
$${(a, b)_n + (c, d)_n = d a n + b c n \text{mod} bd}$$
ちょっと改造すると、また違った整数列(図)が現れる。
$${(a, b)_n \# (c, d)_n = d a n + c n \text{mod} bd}$$
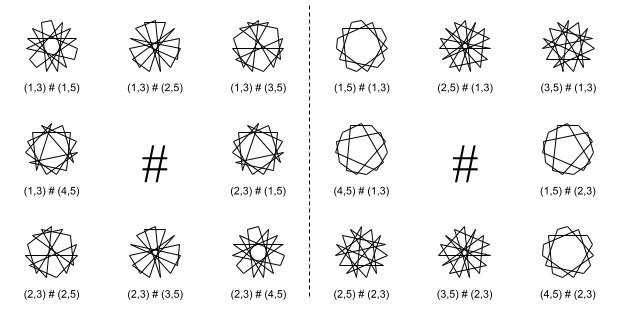
他にも、周期的な整数列であればいいのだから、LCGsからも図が描けたりする。

うーん。美しいなぁ。
