DirectXで内積と外積を探る

ゲームプログラミングで線形代数を学習すると、はじめに現れるのが「ベクトル」ではないでしょうか。実際にゲーム中のキャラクタの移動やキャラクタ同士の位置関係を調べたりするのに、ベクトルはなくてはならないものの一つでしょう。ベクトルの演算の中で使用頻度が高いけれど、何かよくわからないものとして「内積と外積」があります。本稿では内積と外積をDirectXを使用してその特性を探ってみましょう。

ベクトルの内積

ベクトルの演算はベクトル同士の加算、減算はできますが、ベクトル同士の除算はできません。ベクトルの乗算は可能ですが、乗算にはベクトルの内積(dot product)と外積(cross product)が存在します。
では、ベクトルの内積の使い方から説明しましょう。

２つのベクトル間の角度を計算する

内積の特徴として、２つのベクトル間の角度を計算することができます。次の例ではベクトルv1とベクトルv2の２つのベクトル間の角度を計算しています。

内積で2つベクトルのなす角度を計算する

DirectXTKのSimpleMathを使用して２つのベクトル間の角度を内積を使って計算してみましょう。

#include "C:\DirectXTK\Inc\SimpleMath.h"
#include <iostream>

int main()
{
	// ベクトルv1
	DirectX::SimpleMath::Vector2 vectorV1(2.0f, 2.0f);
	// ベクトルv2
	DirectX::SimpleMath::Vector2 vectorV2(2.0f, 0.0f);
	// ベクトルv1の大きさを計算する
	float lengthV1 = vectorV1.Length();
	// ベクトルv2の大きさを計算する
	float lengthV2 = vectorV2.Length();
	// 内積を計算する
	float dotProduct = vectorV1.Dot( vectorV2) / (lengthV1 * lengthV2);
	// アークコサインを計算する
	float radian = acosf(dotProduct);

	// ベクトルv1の大きさを表示する
	std::cout << "VectorV1 length: " << lengthV1 << std::endl;
	// ベクトルv2の大きさを表示する
	std::cout << "VectorV2 length: " << lengthV2 << std::endl;

	// 内積を表示する
	std::cout << "     Dot product: " << dotProduct << std::endl;
	// ラジアンを表示する
	std::cout << "          Radian: " << radian << std::endl;
	// 角度を表示する
	std::cout << "          Degree: " << 180.0f / 3.14f * radian << std::endl;
}

２つのベクトル間の内積の実行結果は次のようになります。

VectorV1 length: 2.82843
VectorV2 length: 2
     Dot product: 0.707107
          Radian: 0.785398
          Degree: 45.0228

2Dの内積と外積の特性を考察する

DirectXを使用して２Dのベクトルの内積と外積の特性を調べてみましょう。

2Dの内積の計算

2Dの内積と外積の計算式を考察してみましょう。内積の計算は「2つのベクトルのx成分同士を掛けた値とy成分同士を掛けた値を加えた値」となります。次に内積の計算式を示します。

2Dの内積の計算式：
v1・v2 = x1 × x2 + y1 × y2 = |v1| |v2| cos(θ)

この計算の特性を理解し易くするためにDirectXを使用して内積の計算をビジュアル化してみましょう。
Githubからダウンロードした「DotCrossProduct」プログラムを実行すると、「←」「→」キーを押し下げるとベクトルv1が回転します。「↑」「↓」キーを押し下げるとベクトルv2が回転します。「ベクトルの内積の計算結果を描画させたいときは、「Shift」を押しながらキー入力」を行ってください。
「ベクトルv2がベクトルv1より前方向に存在する場合(内積の計算結果>0)は、ベクトルv2は「赤色のベクトル」で描画されます。反対に「ベクトルv2がベクトルv1より後方向に存在する場合(内積の計算結果<0)には青色のベクトル」で描画されます。因みに、「ベクトルv1とベクトルv2の角度が直角(90°)になる場合は内積の計算結果はゼロ」になります。
この性質を応用すると、「ベクトル同士の直角判定」「敵や各種オブジェクト位置の前後関係を判定」を行うことができます。

ベクトルv2がベクトルv1より前方向に存在する場合は赤色ベクトルで描画される
ベクトルv2がベクトルv1より後方向に存在する場合は青色ベクトルで描画される

2Dの外積の計算

2Dの外積の計算は「１つ目のベクトルのx成分と2つ目のベクトルのy成分を掛けた値から2つ目のベクトルのx成分と1つ目のy成分を掛けた値を引いた値」となります。次に外積の計算式を示します。

2Dの外積の計算式：
v1×v2 = x1 × y2 - x2 × y1 =  |v1| |v2| sin(θ)

外積の計算結果をビジュアル化してみましょう。GithubからダウンロードしたDotCrossProductプログラムを実行すると、ベクトルv1は「←」「→」キーを押し下げると回転します。ベクトルv2は「↑」「↓」キーを押し下げると回転します。
「ベクトルv2がベクトルv1より右方向に存在する場合(外積の計算結果>0)には、ベクトルv2は赤色のベクトル」で描画されます。反対に「ベクトルv2がベクトルv1より左方向にある場合(外積の計算結果<0)には青色のベクトル」で描画されます。因みに「ベクトルv1とベクトルv2の角度が平行になる場合は外積の計算結果はゼロ」になります。
この性質を応用すると、「ベクトル同士の平行判定」「線分と線分の交差判定」「多角形の内部点の判定」「敵位置の左右判定」などに利用することができます。

ベクトルv2がベクトルv1より右方向に存在する場合は赤色ベクトルで描画される
ベクトルv2がベクトルv1より左方向に存在する場合は青色ベクトルで描画される

「DotCrossProduct」プロジェクトは下記のGithubサイトからダウンロードすることができます。

GitHub - ShozoTanaka/DotCrossProduct

プログラムを実行することができたら、上下左右キーを押し下げて２つのベクトルの位置を移動させ、ベクトル位置の前後左右の判定を検証してみましょう。

内積の正射影

内積が持つ機能として「一つのベクトルからもう一方のベクトルに向けて正射影(Orthogonal Projection)を行う」ことができます。正射影とは「内積の正射影」の図のようにベクトルv1に対してベクトルv2の真上から光を当てたときにできる影(赤いベクトル)のことです。

内積の正射影

鋭角でも鈍角でも

「鈍角の場合にはベクトルv1の反対側に射影される」の図のように、正射影のベクトルはベクトル間の角度が鋭角でも鈍角でも作成することができます。

鈍角の場合にはベクトルv1の反対側に射影される

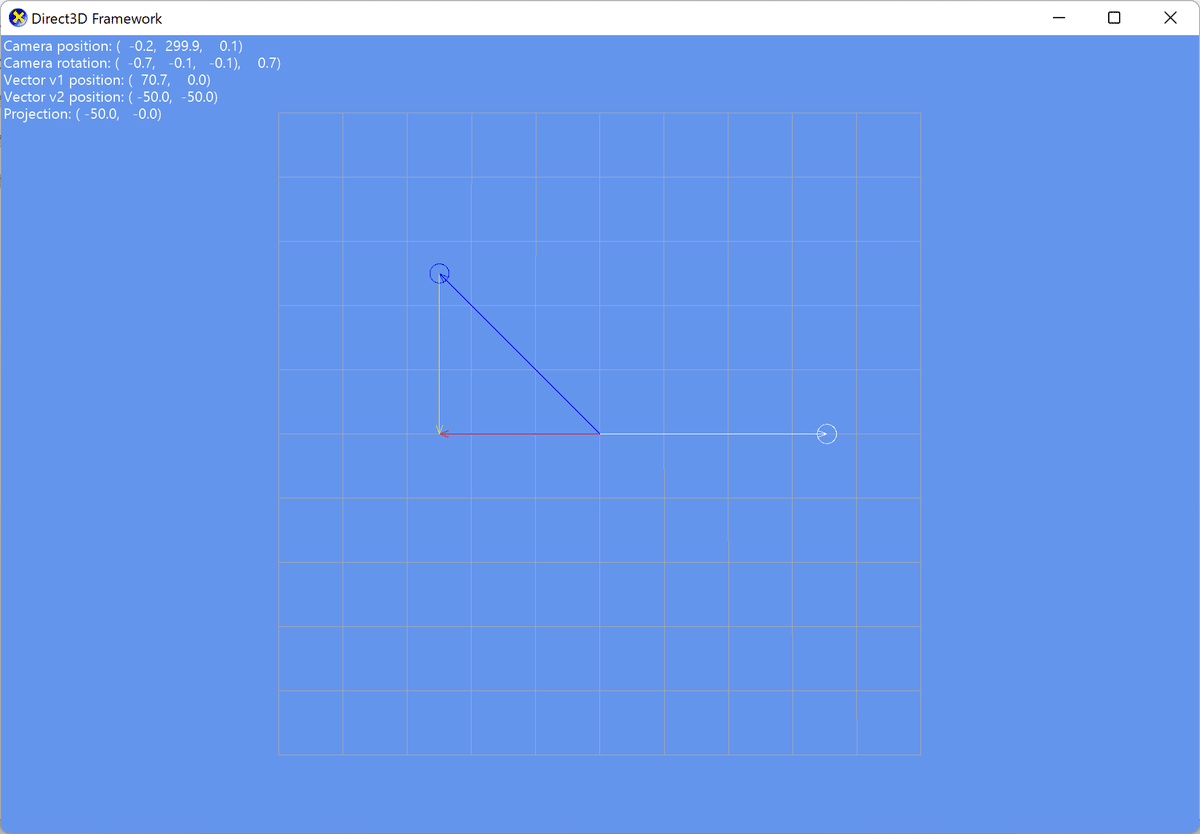
２つのベクトルの位置が変化しても

「２つのベクトルの位置が変化した場合」の図のように、２つのベクトルがどのような位置関係になっていても、１つのベクトルをもう一方のベクトルに正射影を行うことができます。

２つのベクトルの位置が変化した場合

内積の正射影は、２D、３Dを問わずオブジェクトの位置関係を判断したり、様々なオブジェクトの当たり判定で使用されます。

本稿で紹介した「DotProductAsProjection」プロジェクトは下記のGithubサイトからダウンロードすることができます。

GitHub - ShozoTanaka/DotProductAsProjection: Dot product as Projection

プログラムを実行することができたら、上下左右キーを押し下げて、２つベクトルを移動させて、正射影ベクトルがどのように変化するかを検証してみましょう。