レンズの公式（写像公式）について

2020年3月24日 20:22

中学や高校の物理では凸レンズや凹レンズが作る像がどこにできるか、レンズの焦点距離や物体までの距離を用いて導くレンズの公式（写像公式）を学習します。レンズと物体の距離を a 、レンズと像の距離を b 、そしてレンズの焦点距離を f としたとき、以下の各公式がレンズの公式（写像公式）と呼ばれるものです。

（凸レンズの場合で物体が焦点距離よりも遠くにある場合）
　　　1/a + 1/b = 1/f
（凸レンズの場合で物体が焦点距離よりも近くにある場合）
1/a - 1/b = 1/f
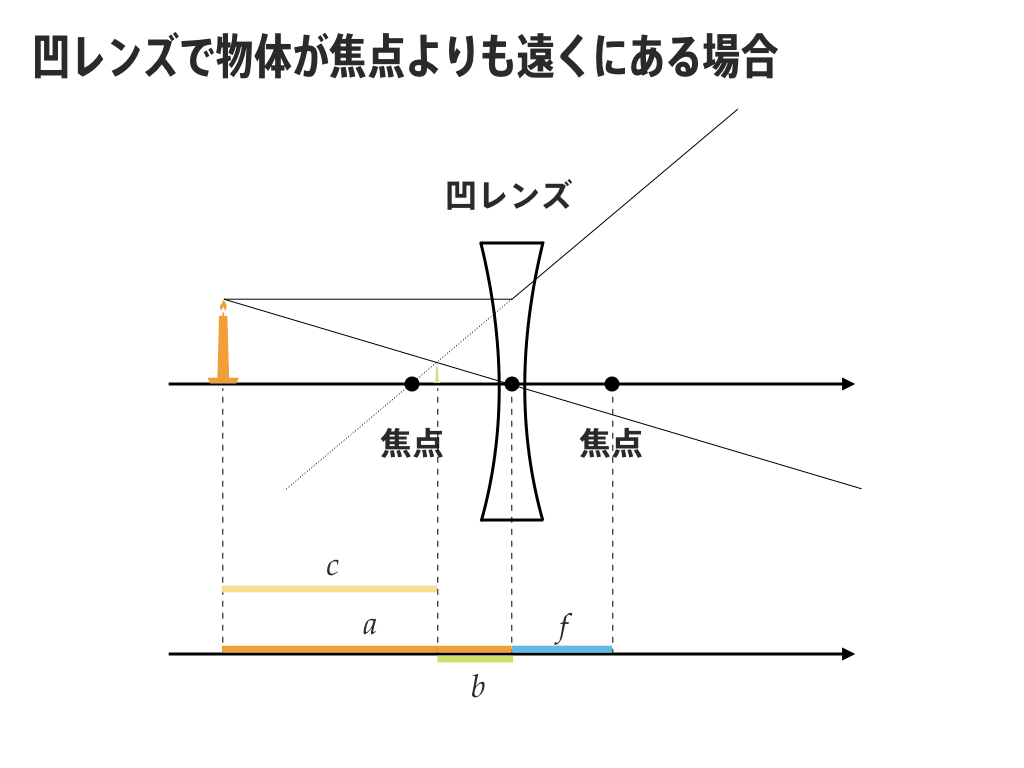
（凹レンズの場合）
1/a - 1/b = - 1/f

ですが、これら 3 つの場合ををそれぞれ覚えておくのは大変です。そもそも、「何で凹レンズの場合には式が 1 つだけなの！？」という質問も出てきてしまいます（まぁ、答えは凹レンズの場合には物体を焦点距離より近くに置いても遠くに置いても虚像ができるからなのですが……）。そこで、これらの公式を 1 つにしたいなと思うわけです。1 つにしましょう。レンズの公式の説明のなかには、b や f に負の値を担わせて（すなわち -b や -f として考える、あるいはこれらの値に絶対値を付けることによって）式を 1 つにしているものも見受けられます。まぁ、気持ちも分かります。ですが、これはどういう場合に + になって、どういう場合に - になるのか、場合分けしているのと同じです。覚えることはちょっと少なくなりますが、1 つにできているわけではありません。

私がここで教える方法は、本当の意味で式を 1 つにできていると思います。ただし、正しい図を書かなくてはいけません。場合分けは図に担わせます。ですが、みなさんはわりと作図するのは得意なようです。

焦点距離 (f) ＝レンズと物体の距離 (a) × レンズと像の距離 (b) ÷ 物体と像の距離 (c)

この式なら、次に示すどの場合にも適用できます。すべて距離ですから、正の値しか代入できません。レンズのどちら側に像ができるかは図が教えてくれるので、図で判断しましょう。とは言え、距離が 4 つもあるので、どの距離がどこに当てはまるのかを覚えるのは大変かもしれません。そこを少し楽にするために、次のような覚え方にしています。

焦点距離 (f) ＝レンズと○の距離 × レンズと△の距離 ÷ ○と△の距離

左辺が焦点距離 (f) であるというのは覚えなくてはいけません。右辺には 3 つの距離が登場しますが、分子の 2 つはレンズが基準です。レンズと何かの距離を 2 つ掛け算すればOK、当然レンズと物体、レンズと像になります。そして分母はレンズを無視して、物体から像までの距離というわけです。どうでしょう。少しは簡単にできたでしょうか。

なお、倍率 (m) は教科書に載っている次の公式がそのまま使えます。