
コンサルタントの「問題解決」ノート術 #3:誰も教えてくれない本当のロジカルシンキング
みなさんは、これまでさまざまな問題に対して、これまたさまざまな問題解決を図ってきたはずです。問題解決手法というのもたくさんあるので、いろいろ試したりしているかもしれません。
まずは代表的なロジックツリーとマインドマップが問題解決には不向きであることを説明し、その後で問題解決に不可欠なロジカルシンキングの3つのステップを解説します。
You see there is only one constant. One universal. It is the only real truth. Causality. Action, reaction. Cause and effect.
不変の真実がある。すべてを支配する唯一絶対の真実がね。因果関係だ。作用 反作用 原因と結果。
メロビンジアン 『マトリックス・リローデッド』より
ロジックツリーは使える?
たとえば、ロジカルシンキングの基本中の基本と呼ばれるツールに「ロジックツリー」というものがあります。「イシュー」と呼ばれるボックスを起点に、複数のボックスが樹状につながったチャートがロジックツリーです。
イシューとは,「論点」とか「議論上の争点」のことです。
イシューのボックスから、その問題を「どうやって?」と解決策を考え、いくつかのボックスに枝分かれして記述していきます。このとき、MECE(Mutually Exclusive and Collectively Exhaustive)でモレなくダブリなく網羅的に考える事が大切とされています。
たとえば、「売上を向上させる」というイシューについて考えてみましょう。
2段目のボックスは、「顧客数を増やす」と「顧客単価を増やす」の2つ解決策が考えられます。次に、それぞれのボックスについて「どうやって?」をさらに考えてみます。「稼働顧客数を増やす」のボックスは、3段目として「新規顧客を獲得する」と「既存顧客のリピート率をあげる」に分けて考えることができます。2段目のもう一方のボックス「顧客単価を増やす」は、「高額商品をラインアップに加える」と「低額商品を加えてついで買いを促進する」に分けて考えることができます。
このように、上位のボックスを「どうやって?」と下位のボックスに分解して解決策を網羅的に列挙していくのがロジックツリーです。

どこかで見た事があったり、実際に使ってみたりしたことがありますか?
本当に問題を解決することは出来ましたか?
「ロジックツリーは使えない」と思っている方も多いのではないでしょうか。
概念・事象をある切り口で因数分解し、論理的なつながりを樹状に図示するロジックツリーには、実は大きな欠点があるのです。
ロジックツリーの欠点、その1
1つ目の欠点は、最下位の解決策全てを実施してしまうことです。
MECEで分解して導き出した解決策ですから、どれもが正解のはずです。どれを実行してどれを実行しないか甲乙つけ難いために、ついついすべてを実行してしまうのです。そうなるとやたらに忙しくなってしまい、十分な成果を待たずに次々手を付けて、いったい何が成果につながったかわからなくなることもしばしばあります。
さらに悪いのは、ある解決策が解決すべき他のボックスに副作用を与え、成果が出ないどころか逆にパフォーマンスを悪くする結果にもなりかねないのです。
ロジックツリーの欠点、その2
2つ目の欠点は、「切り口」をどのように設定するかでロジック・ツリーの広さや深さが決まることです。
複数の切り口がある場合は、同じイシューに対して異なる切り口のロジックツリーを作ることになりますし、切り口が適切でなければたとえどんなに素晴らしい解決策を見つけても、それが成果につながらない場合もあります。
ロジック・ツリーで問題解決を図るためには、実は相当”勘”が良くなければならないのです。
”ロジック”という語句が付いたツールなので、これを使えばロジカルシンキングが出来ていると思いがちですが、実は必要条件だけ書き出して十分条件を満たしていないとか、分類をしているだけで因果関係が考慮されていないとか、ツールとしては使いこなすのが難しい部類になります。
この2つの欠点があることにより、ロジックツリーで導いたたくさんの解決策を実施してその成果を寄せ集めても、そもそもの発端であったイシューの解決にならないことが多いのです。
マインドマップは使える?
今度は、マインドマップについて考えてみます。
マインドマップはトニー・ブザンが提唱した思考・発想法の一つで、表現したい概念の中心となるキーワードやイメージを中央に置き、そこから放射状に連想したキーワードやイメージを周辺に拡げて描いていくものです。
イラストが入っていたり、とてもカラフルな出来映えになることも多く、子供から大人まで気軽に使えて、発想を豊かにし、記憶力を高めるために思考を整理、展開していきます。そもそもの目的が、イマジネーションと連想を用いて複雑な概念を可視化して記憶したり、自分自身の外界の捉え方を明確にして他人と共通認識を図るのが、マインドマップです。

戦略フレームワークのような使い方をたまに見かけますが、ツールの目的とは本来かけ離れているのを知らずに使う人も多いようです。
マインドマップは、その書き方自体が、人間の脳の意味記憶の構造によくマッチしているので理解や記憶がしやすいと言われています。
先の記事で書いた、書き出すことの4つのパワーのうち、1つ目の記憶の錯覚を避けることと3つ目の共通認識を持つことを兼ね備えていますが、連想や想像が元になっているので、ロジカルではないし、人格との分離もされないという特徴があります。
要は、ツールは使いようで、マインドマップはそもそも整理力、想像力、記憶力を高めるものであり、問題解決のツールではないので、マインドマップを使って解決策を見出そうというのはちょっと難しそうですね。
多くのフレームワークは、分類が目的
他にも、ロジカルシンキングでよく出てくる、特にビジネスにおいて使われるフレームワークには、
3C(Company、Customer、Competitor)
マーケティングの4P(Product、Place、Price、Promotion)
5フォース(買い手、供給業者、新規参入者、代替品、業界内の競争)
SWOT(強み、弱み、機会、脅威)
など多数あります。
これらはすべて物事を「分類」するためのフレームワークです。
これはこれでとても役に立つし、必要不可欠なのですが、ロジカルシンキングで網羅すべきは、この「分類」の他に、「相関関係」と「因果関係」があります。「分類」は、ロジカルシンキングの第一歩に過ぎないのです。
以前、四大会計ファームの社内研修で使われているロジカルシンキング研修資料を全部読んだのですが、MECEとロジック・ツリーを教えているだけでした。
それでは、ロジカルシンキングの3つのステップを説明していきます。
ロジカルシンキング ステップ1:分類
ステップ1の思考法である「分類」については、リチャード・ソール・ワーマン(1984年にTEDを創立したことでも有名)が著書の中で「たった5つだけ」と言っている手段がありますので、これをご紹介しましょう。
5つの究極の整理棚として紹介されているのは、「LATCH」。
Location(場所)
Alphabet(五十音順)
Time(時間)
Category(分野)
Hierarchy(階層)
5つの手段の頭文字を取って、通称「LATCH(ラッチ)」と読んでいます。「分類」は、この5つと、分類するときの粒度(細かさ)と、MECE(モレ無くダブリ無く)を心掛ければ、難しくはありません。
たとえば、イチゴを例にとって、この「LATCH」を使ってみましょう。イチゴの品種には、アイベリー、あかねっ娘、あきひめ、あすかルビー、あまおう、あまおとめ、あまみつ、淡雪、かおり野、クィーンレッド、久能早生、恋の香、古都華、さがほのか、さくらももいちご、さちのか、さぬきひめ、サマープリンセス、スカイベリー、桃薫、とよのか、とちおとめ、女峰、農姫、ひのしずく、紅つやか、紅ほっぺ、宝交早生、まりひめ、もういっこ、ももいちご、やよいひめ、ゆふおとめ、ゆめのか、麗紅、レディア、ロイヤルクイーンなどがあります。
Alphabet(五十音順)による分類は、まさに前述したのが五十音順なので、ア行カ行と分類してみたり、”あま”や”紅”などキーワードでグループを作ってまとめることもできます。
最近見かけるようになったスカイベリーは、栃木県で品種改良され、栃木県で生産されています。女峰は、栃木県で品種改良され、栃木県だけでなく静岡県と香川県で生産されています。Location(場所)で分類するとしたら、品種改良地で区分したり、生産地で区分することができます。
品種登録時期で分類するのは、Time(時間)です。女峰(にょほう)は1985年の登録で、スカイベリーなら2014年の登録だったりします。
Category(分野)は、粒の大きさや糖度や色合いなど様々な切り口が考えられます。一般的な商品区分などは、すべてCategoryに当たります。
Hierarchy(階層)は、重要度や優先順位などで上位と下位を区分するのが一般的です。
イチゴの場合は、交配元となった品種で分類することもできるでしょう。たとえば、”さちのか”は「とよのか」に「アイベリー」を交配していて、”さがほのか”は「大錦」に「とよのか」を交配していますから、交配元(親)である「とよのか」つながりの兄弟種として分類できます。
複雑に思えるたくさんの事柄を、まずは整理して理解しやすくするのが「分類」なのです。
ロジカルシンキング ステップ2:相関関係
ビジネスシーンでも「相関関係」は、比較的よく使われるものなので、皆さんも馴染みが深いと思います。
エクセルでデータ分析をするときに、散布図に回帰直線を重ねて、相関係数を出したことがあることでしょう。統計学をあまり知らなくて相関グラフが作成できる便利な時代です。
ところが、簡単にグラフが作成できるのと裏腹に、相関関係は間違った結論を導くことにもなりかねないので注意が必要です。
たとえば、横軸にアイスクリームの売上個数を取り、縦軸に水死者数をとったとします。ある年の日本で、集計した2つの日毎のデータをグラフにプロットし、回帰直線を引いてみると、見事な相関関係が見られます。しかし、相関関係が高いからといって、「アイスクリームが売れれば、水死者が増える」という結果を導く人はひとりもいないでしょう。直感的におかしいことがわかりますよね。
では、こんな事例はどうでしょうか?
ホルモン補充療法を行っている女性を対象に疫学調査が行われ、その結果、ホルモン補充療法を受けている女性の冠状動脈性心臓病の発症率が低いことがデータ分析によって判明しました。このことにより、ホルモン補充療法は冠状動脈性心臓病予防に効果があると提案されたのです。
誰もがなるほどと思う結果ですが、このデータを詳しく調べてみると、ホルモン補充療法を受けているのは上流階級の女性であり、彼女たちはそもそも健康に対する意識が高く、ダイエットやエクササイズなど健康増進のための様々な行動をかなりの頻度で行っていることがわかりました。
つまり、ホルモン補充療法と冠状動脈性心臓病には、相関関係はあったのですが、原因と結果の関係は存在していなかったのです。
データを駆使して複雑な回帰分析をしていると、いたるところに相関関係を見出すことが出来ます。相関関係があれば、二つの事柄になにかしら関連性があると判断するのは当然です。
さて、ここで演習です。
ホルモン補充療法と冠状動脈性心臓病にはどんな関係があるか、図で描いてみましょう。
このふたつの事柄に、原因と結果の関係はなく、相関関係はあるということはわかっています。先の文章をよく読むと、共通の「別の原因」があることがわかるはずです。「ホルモン補充療法」と「冠状動脈性心臓病」と「別の原因」の3つの関係を、矢印を使って描いてみてください。また、別の原因が何であるかも、自分の言葉で書いてみましょう。

解答はこちらです。

では、次の演習です。
アイスクリームと水死者にはどんな関係があるか、図で描いてみましょう。このふたつの事柄に、原因と結果の関係はなく、相関関係はあるということはわかっています。ホルモン療法の演習と似ていますが、ふたつに共通する「別の原因」を描き加える必要があります。「別の原因」がなにか、自分の頭で考えて図解してみて下さい。

ここで覚えて欲しいのは、「相関関係は因果関係を含意しない (Correlation does not imply causation)」ということです。
言い換えれば、「相関関係は因果関係と同じではない。相関関係は因果関係の必要条件の1つである」ということです。観察によって特定のパターンが見出せる時には相関関係があると言えますが、因果関係があるとは限らないことに注意しましょう。このことは、相関関係は偶然の一致によって起こっている場合があることも示しています。
ロジカルシンキング ステップ3:因果関係
最終段階のステップ3は、「因果関係」です。
物事を原因と結果に分けて考える科学的アプローチそのものだと言えます。最終段階と言われるとなんだかやたらに難しそうに思える「因果関係」ですが、小さな子供が「なぜ、お空は青いの?」と聞くのと同じですので、大人に出来ないわけがありませんね。
因果関係について、先の「相関関係」で描いた図を元に考えていきましょう。
アイスクリームの売上個数と水死者数の関係を、「別の原因」を描き加えて表現できたでしょうか?
まず、「別の原因」は「気温」です。もし気温が上昇するならば、アイスクリームの売上個数が増加します。同様に、もし気温が上昇するならば、涼を取るために水遊びをする人が増えるために確率的に水死者数が増えることになります。
これを図解すれば、「気温が上昇する」というボックスから「アイスクリームの売上個数が増える」ボックスと「水死者数が増える」ボックスそれぞれに矢印を引いて表現することができているはずです。矢印は、因果関係の存在を示し、原因から結果へ向かって書くのが作法です。
ボックスの中味をより汎用的な表現にするならば、「気温」「アイスクリームの売上個数」「水死者数」という変数として書いてもいいでしょう。

こうやって図解してみると、「相関関係」と「因果関係」の違いは明白です。
Xという原因があるときに、Aという結果(現象)が起こる。
また、Xという原因があるときに、Bという別の結果(現象)が起こる。
XとA、あるいはXとBには因果関係が存在しますが、AとBの間に因果関係はありません。
共通の原因であるXによって引き起こされたAとBを同時に観測したときに、AとBの動きに関連性をもったパターンがある場合に、相関関係が存在すると認識されるわけです。つまり、相関関係は、同じ原因で起こった複数の現象の関係を表していると言えます。
もうおわかりのように、日々の業務の中で相関関係と因果関係を混同してしまうと、冠状動脈性心臓病予防のためにせっせとホルモン補充療法を行ってしまうように、結果を生まない原因を戦略や施策として立案・実行し、時間と費用を浪費してしまうことにもなりかねないのです。
思い当たることはありませんか?
では、どうすればいいのでしょうか?
相関関係と因果関係を間違えず、きちんと因果関係を捉えられるようになるには、何を学べばいいでしょうか?
相関関係と因果関係を見分ける簡単な方法
まずは、図解からスタートです!
アイスクリームやホルモン補充療法の演習でも行ったように、数字をすぐに駆使するのではなく、文章で表現するのが第一歩です。
それらしい数字を目の前にするとついついそれに引き摺られて先入観や誤解をしがちなのですが、文章であれば、まずは直感的に間違いを排除することができます。
稚拙な表現でも構わないので、まずは書き出してみましょう。
短期記憶貯蔵庫のマジックナンバーの話しがありましたね。頭の中に溜め込むと途端に難しくなってしまうので、書いては考え、考えては書き直し、何回でも繰り返してみてください。
相関関係と因果関係を見分ける簡単な方法は、3つあります。
一つ目は、共通の原因が存在するかしないか考えます。
これは前述の例でもありました。「気温」は比較的見つけやすかったでしょう。ホルモン補充療法と冠状動脈性心臓病の場合は、そう簡単には共通の原因は見つけられないですが、その時は二つ目のチェックをしましょう。
二つ目は、Aでない時にBが起こらないと言えるかどうかをチェックすることです。
ホルモン補充療法をしない人で、冠状動脈性心臓病の発症率低下が起こっていないか考えてみると、どうも怪しいと直感が訴えかけます。まさにそういうときに、データを再検討すればいいわけです。
三つ目は、時系列で起こっているかをチェックすることです。
因果関係があるなら、結果は原因よりも時間的に必ず後に起こってるはずです。数ヶ月後、数年後という時間的遅れがある場合もありますが、原因と結果の順序が逆になることはありません。単なる相関関係であれば、この時系列の関係が崩れているはずです。
因果関係で徹底的に考える
”決断に必要なのは、誰でもうなずける科学的な根拠である”
本田宗一郎
なんだか段々難しくなってきた…と思っているかもしれませんが、そういう時こそ書いてみましょう。物事の関係を表すのがロジックであり、原因ー結果と組み上げていくのが因果関係です。
一生懸命説明をした後で、「君の話はよくわからない」とか「言いたいことはわかるけど、どうしてそうなるの?」と切り替えされて、グッと詰まってしまったことはありませんか?
逆に、「いやー、君の話でようやくわかったよ」とか「そういうことなのか!」と言わせてみたいですよね。
エレベータに乗り合わせた相手に、目的の階に到着するまでのわずか数十秒で自分の話を伝える”エレベーターピッチ”で、「いいアイディアだ。あとで詳しく聞かせてくれないか」と言われたら、もっと素晴らしいでしょう。
因果関係で徹底的に考える癖がつけば、大丈夫!
因果関係で考える癖がつけば、物事を断片的に記憶するよりも、遙かに多くのことをストーリーとして記憶することができます。また、目の前にある現象からまだ起こっていない結果を推測することが容易になり、確度が増せば「先見性がある」を周りから見られるようになります。
それでは、どんどん書いてみましょう。
因果関係で考える演習問題 その1
まず、一つ目の演習です。
「壁のスイッチのONを押せば、天井の照明がつく」を、原因のボックスと結果のボックスに分けて書き、原因から結果に矢印を引いてみてださい。
たぶん、1分もかからずに書けるはずです。日頃から当たり前のように経験しているので、原因と結果を見分けるのは難しくないでしょう。
読み進めるまえに、ここで立ち止まり、必ず図解してください。

ところで、なぜ矢印で結びつけることができるのでしょうか?
このつながりの裏にあるものを考える事がとても大切です。
原因と結果を結びつけている”理由”が何かを考えてみて下さい。経験的に知っているし、理系の人なら専門的な理由が思いつくでしょう。けれども、他人にわかるように理由を書くことがポイントです。
簡単そうに思えても取っ掛かりがないと感じるなら、ロジカルシンキングレベル1の「分類」でまずは整理してみましょう。
原因と結果を結びつける理由を探すなら、この例題の場合は「壁」「天井」「壁と天井の間」に分けることができます。LATCHを覚えているでしょうか?
そうです、Locationで分類しています。
この例では、原因は「壁のスイッチのONを押す」であり、結果は「天井の照明がつく」です。

原因として書いた「壁のスイッチのONを押す」のボックスの横に、「壁」「天井」「壁と天井の間」にありそうな理由を並べて書いてみてください。
次に、レベル2の「相関関係」をチェックしてみましょう。
チェックポイントの一つ目、共通の原因は存在しているでしょうか?
どうも無さそうですね。
チェックポイント二つ目、Aでない時にBが起こらないか考えてみましょう。
常識的には、壁のスイッチのONを押さない、つまりOFFのままであれば、天井の照明はつかないですね。どうやら相関関係に留まらず因果関係がありそうです。
チェックポイントの三つ目、時系列で考えてみるとどうでしょうか?
天井の照明がついたその後に壁のスイッチがONになるわけではないですから、やはり因果関係があると言うことができます。
改めて、「天井の照明がつく」という現象を引き起こす原因と理由を考えてみましょう。
「壁」には、「ONスイッチは電気を流す」という理由が思いつくでしょう。「天井」には、「電球が切れていない」という理由があるはずです。「壁と天井の間」には、「スイッチと照明器具が電源コードがつながっている」という理由があります。
原因があれば、結果が起こる。
言い換えれば、原因が発生することで何かが変化するわけです。変化が起きる理由として、「ONスイッチは電気を流す」「電球が切れていない」「スイッチと照明器具が電源コードがつながっている」の3つを見つけました。
これら3つの理由は、原因があろうがなかろうが存在しているという性質を持っています。
このような理由は、一般的に「前提条件」と呼ばれ、日常的にほとんど意識していないという特徴を持っています。また、「前提条件」は、ひとつでも欠けると、原因が与えられても結果が起こらないという特徴もあります。このような前提条件は、別名「常識」とも呼ばれます。

何気なく描いた矢印には理由が隠れています。
慣れるまでは、自明だとして矢印で済まさずに、原因と理由を横並びに描いて、それぞれから結果に向かって矢印を引き、矢印の上に円弧を重ねて描いてみましょう。この円弧は、「AかつB」という十分条件であることを示す記号で、結果が生じるために全て同時に存在しないといけないことを表していると覚えておいてください。
また、このような書き方をした場合は、理由も原因のひとつとして扱うことができます。


ところで、この例題を出すと決まって出てくる質問は、「電気が流れると照明がつく理由はどうすればいいですか?」というようなものです。
これは、とても鋭い質問です。
「壁のスイッチのONを押せば、天井の照明がつく」の理由を、電気の存在を知らない人に説明したら、わかってもらえないですね。
照明器具の原理や構造を知っている人には、先の演習で書いた理由で十分ですが、そうではない人に対しては、もっと詳細な説明をする必要があります。
では、どこまで詳細な説明をすればいいのでしょうか?
究極まで詳細な理由を述べていくと、素粒子やビックバンまで辿り着かなければいけないかもしれません。
でも、答えはシンプルに、「相手が納得してくれるまで」です。
同じ程度の知識レベルをもち、同じような文化的背景を持ち合わせている相手であれば、前提条件そのものは暗黙のうちに共有しているので、詳細な説明は不要です。逆に言えば、知識レベルが異なる相手、文化的背景が異なる相手には、この前提条件を「常識」として説明を省いてしまうと、話しがまるで通じないということに納得できるでしょう。
異文化コミュニケーションの難しさはまさにこれですし、親子の会話や上司と部下の会話でどうも噛み合わない時には、前提条件を共有していないことがほとんどなのです。
だから、因果関係で考え、理由を明確に意識するロジカルシンキングは、コミュニケーションを円滑にすることが出来るのです。
説明がまどろっこしかったかもしれませんので、次からは演習と答えだけにしましょう。
因果関係で考える演習問題 その2
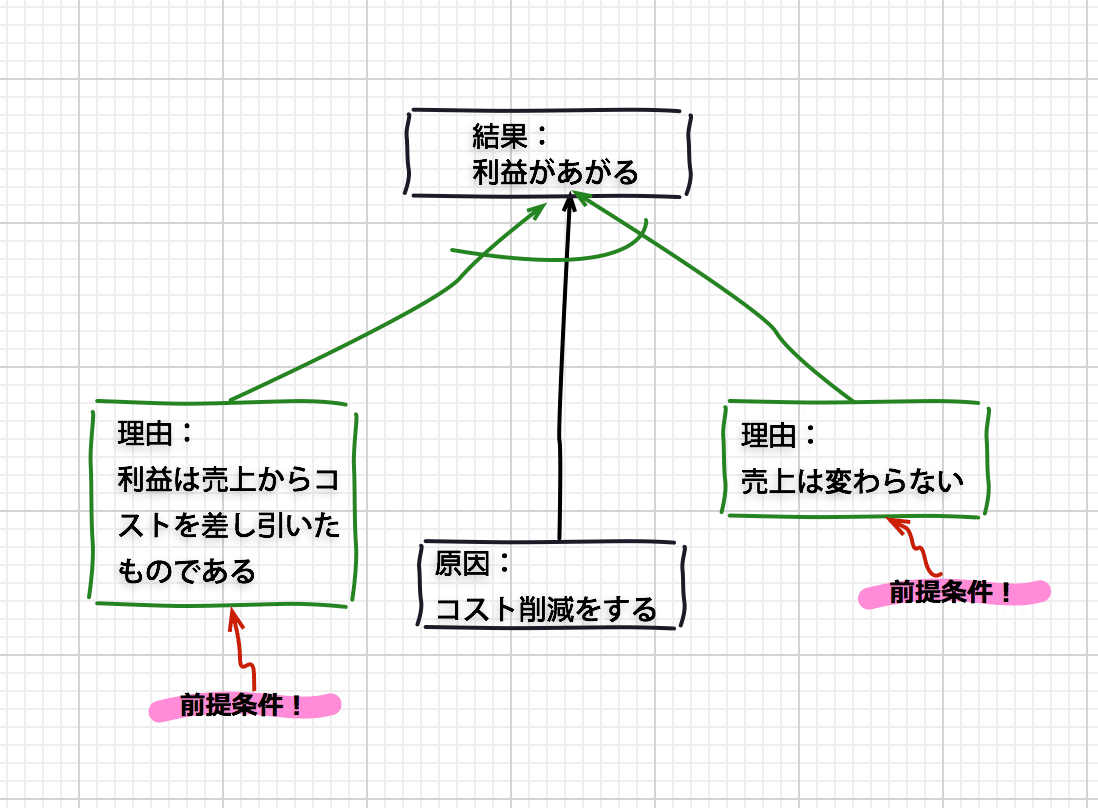
「利益をあげるために、コスト削減をする」という文章を、因果関係で描いてください。
そして、その理由も描いてください。
書き終わったら、読み進めて下さい。

解答はこちら。

ちょっとひねった例題ですが、この表現は「必要条件」を表しています。物事のつながりの異なる捉え方として「因果関係」と「必要条件」という表現ができるわけです。
先ほど、因果関係で考える際に「理由」を洗い出しました。「必要条件」で考えると、これらの理由は「十分条件」にあたります。照明の例題で説明すれば、「天井の照明がつく」ためには、「ONスイッチは電気を流す」「電球が切れていない」「スイッチと照明器具が電源コードがつながっている」、それに「壁のスイッチのONを押す」が揃っていないと十分ではないということを示しています。
さて、演習に戻りましょう。
原因は「コスト削減をする」であり、結果は「利益があがる」となります。
理由はどんなものがでてきましたか?
この場合の前提条件は、ビジネスパーソンを対象にするならば、コスト構造に関するものが出てきたはずです。
「売上は変わらない」「利益は売上からコストを差し引いたものである」が出てきたでしょうか。
ロジックとは、膨大な知識のことである
原因と結果を結びつける理由、つまり因果関係を結ぶためには、知識が必要になることに気づいたのではないでしょうか?
「壁のスイッチのONを押せば、天井の照明がつく」という演習の時に、電源コードと電気の存在を知らなければ、因果関係の矢印を結ぶことはできません。
「利益をあげるために、コスト削減をする」という演習の時には、コスト構造の定義を知らなければ、因果関係の矢印を結ぶことはできません。
このように、ロジックというのは理由に相当する知識のことなのです。
「あの人はロジックが強い」という言い回しをすることがありますが、つまりは「あの人は膨大な知識を持っている」ということです。
逆に理由に相当する知識が乏しいのに物事を結びつけて考える事は、連想であり、想像ということになります。優劣があるわけではありませんが、使い分けることが大切になります。
まとめ
ロジカルシンキングはロジックツリーに代表される「分類」の他に、「相関関係」と「因果関係」があります。また、相関関係と因果関係を見分ける方法が3つあることや、因果関係を図解する作法を説明してきました。
徹底的に因果関係で考えることが本当のロジカルシンキングです。
#4では、因果関係で表したものをチェックする方法を説明していきます。
サポートのお気持ち、感謝いたします。 ぜひその分を自分自身に投資して、記事を参考になにか新しい事にチャレンジしてください。その成果をお知らせいただけるのが、一番の報酬です!
